What Memes Are Perfect for AP Calculus AB/BC?
5 min read•july 11, 2024
C
Catherine Liu
AP Calculus AB/BC ♾️
279 resourcesSee Units
Keeping up with the fast and challenging curriculum of AP Calculus can be hard to handle sometimes. Looking at calculus memes can help you understand complex topics in a more enjoyable way. These ten memes have humorous and educational aspects that will help you better understand AP Calculus.
Meme #1

Image Courtesy of Nerdy Jokes Tumblr
Your calculator can only be in two different modes: degrees or radians. This joke is referencing the fact that if you’re not in degree mode, you’re in radian mode. RAD is the abbreviation for radian mode.
In AP Calculus class, knowing what mode to have your calculator in is crucial for calculating trigonometric values. Something most students don’t know is that the mode of your calculator only matters when using trigonometric functions such as sine, cosine, tangent, secant, cosecant, or cotangent. With every other calculation, you’ll get the same answer regardless of which mode you’re in. Here’s a simple breakdown of when you should be using each mode:
Degrees:
- When you're using degrees as a unit.
- If the question is sin(48°), then your calculator needs to be in degrees.
- If your input (which is 48 degrees in the above example) is in degrees, then your output needs to be in degrees.
Radians:
- When you’re using radians as a unit.
- If the question is sin(3𝝅/4), then your calculator needs to be in radians. Keep in mind that a number doesn’t need to have a pi symbol to be in radians
- If your input (which is 3𝝅/4 in the above example) is in radians, then your output needs to be in radians.
For more calculator tips, check out "What Calculator Functions Will Save Your Life?"
Meme #2
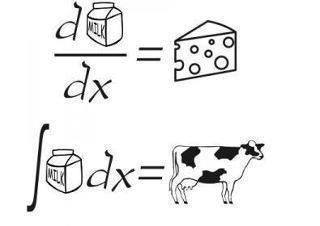
Image Courtesy of Architecture & Civil Engineering Facebook
One of the most important things to know about calculus is the relationship between derivatives and integrals. To put it simply, an integral is an “opposite” derivative. This joke is a classic example of the concept. If you derive the milk, you get cheese because that is the next step of the process. If you integrate milk, you get a cow because that is the previous step in the process. In this situation, the process is cow → milk → cheese.
For some more help with understanding derivatives, check out this set of guides! What about integrals? Check out this set!
Meme #3 and #4


Images Courtesy of Erica S Pinterest and 9GAG.com
When learning about derivatives, you’ll most likely have to memorize the derivatives or certain functions like natural logs and trig functions. One of the easiest derivatives to remember is that the derivative of e^x is e^x.
In the first meme, it shows how the natural log function was changed into a 1/x and x^2 function was changed into a 2x. The e^x function was unchanged because its derivative is the same as the function. In the end, it is revealed that the book is a derivative.
Similarly, in the second meme, the man is unchanged despite deriving multiple times. Thus, the only explanation is that he is e^x.
Here’s a chart to help you remember your derivatives:

Image Courtesy of Magoosh AP Calc Prep
Meme #5

Image Courtesy of Bowman Dickson
While this meme isn’t actually calculus-related, I have found that many students still make this mistake from time to time. When I was taking calculus, my teacher couldn’t stand when his students did this. It is crucial to remember that addition and subtraction cannot be treated the same way as multiplication and division when it comes to exponents.
As seen in the meme, most students think that (x^2 +3)^2 equals x^4 + 9 However, the answer is actually x^4 + 6x + 9 because you have to FOIL (first, outer, inner, last). It is important to recognize that (x^2 +3)^2 is the same as (x^2 + 3)(x^2 + 3) not x^4 + 9.
Meme #6

Image Courtesy of Zazzle.com
When deriving the position function, the first derivative is velocity and the second derivative is acceleration. The 3rd derivative, which is shown in the meme as d3x/dt3, is known as a jerk. Thus, the meme says “Don’t be a jerk”.
Meme #7
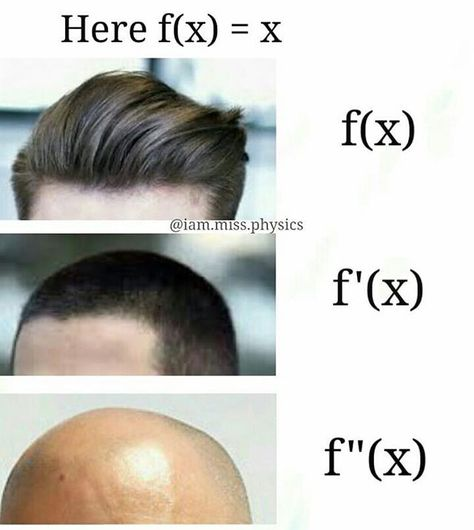
Image Courtesy of @iam.miss.physics Instagram
This meme shows how the original function, f(x), can change drastically after being derived once or twice. In the meme, the first picture of the hair represents the original function. As you can see, the hair gets shorter and shorter similar to how a function’s graph changes when it is derived.
Meme #8 and #9


Images Courtesy of Spiked Math Comics
Both of these memes reference the same concept of calculus. When you’re integrating any function, you must have a “+ C” on the end. As mentioned previously, integration is essentially a reverse derivative. Take a look at this example to better understand this:
15x^2 + 8
If f(x) = 5x^3 +8x + 7 and f’(x) = 15x^2 + 8, then ∫ f’(x)dx should equal f(x). However, ∫ 15x^2 + 8 dx actually equals 5x^3 +8x. The problem here is that constant from the original function (7) isn’t represented.
Thus, it is important to add “+ C” at the end of the function when you integrate so the constant is represented. This “+ C” is an arbitrary constant that can be anything you want, as seen in the first meme.
Meme #10

Image Courtesy of @math.hero Instagram
When you’re first learning about derivatives in AP Calculus class, you’ll likely learn to take a derivative using a limit rather than using derivative rules. To take a derivative using a limit, you must use the difference quotient. The formula for the difference quotient is shown in the speech bubble of the meme. Thus, the difference quotient can be thought of as a derivative’s “full name”.
Closing Thoughts
Hopefully, these memes will help you better grasp the complex concepts of AP Calculus. If you are ever confused, consider talking to your teacher or chatting with us here at Fiveable.
Good Luck with your AP Calculus studying!
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.