How do I take a derivative?
4 min read•july 11, 2024
AP Calculus AB/BC ♾️
279 resourcesSee Units
How to Take a Derivative
So, chances are that you've either started looking at what you need to know for AP Calc to get a head start or you're starting the class and you're completely lost. Fear not, this'll go through the basics and everything you need to know about derivatives!
Check out 🎥 Introduction to Finding Derivatives for more information!
Let's start off with a simple question: What is a derivative?
A derivative is the instantaneous rate of change of a function or slope of a tangent line on a graph, usually denoted by 'd/dx {f(x)}'
With taking a derivative, there are a couple of rules that you'll need to know
Power Rule
- The formula for the power rule looks something like this

- With this formula, 'x' is the variable, and 'n' is the exponent
- First, you have to look at the exponent. It's also important to remember your exponent rules here too (anything to the power of 0 is 1, negative exponents, etc.)
- Next, you need to multiply the coefficient of the variable by the exponent
- The last step is to subtract one from the original exponent. This is now the new exponent for the derivative!
Let's go over a quick example then:

- We can see that the we have an exponent of two and a coefficient of 3.
- Now that we've noted this, we have to multiply the coefficient by the exponent.
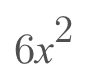
- Last but not least, we have to subtract one from the exponent value

- And voila! You've taken a derivative using the power rule!
Sum and Difference Rule
This rule is pretty straight forward and is used when you're taken a derivative of a function that has multiple terms.
- The rule in its formal form looks like this
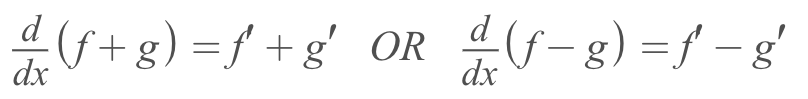
- The first one shows the sum rule while the second one shows the difference rule (That apostrophe means 'the derivative of')
- This one's a pretty easy one to pick up on so we're gonna go ahead an go into the next one! If you need additional practice with this one there'll be some links to some great resources for practice problems.
Product Rule
- This rule is used when two parts of a function are being multiplied by each other (this is different from chain rule!)

- This looks super confusing but the saying my teacher taught me really helped: "first times the derivative of the second plus second times the derivative of the first"
- In this case, the 'first' would be the variable 'f' while the 'second' is the variable is 'g'
- First, you'll need to identify your two variables, pay attention to their coefficients and exponents
- Next, identify which term will be your 'first' and which will be your 'second'
- Now you're going to take the 'first' and multiply it by the derivative of the second and vice versa.
This can get pretty confusing through just words so we'll go over a quick example to help see how it should be done!
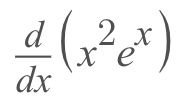
- This first step is to identify our terms. We have 'x^2' and 'e^x' and we can see that they are being multiplied by each other. Now, we'll assume that 'x^2' is going to be our 'first' and 'e^x' is going to be 'second'
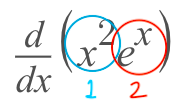
Now, we have to follow through with the formula and saying: "first times the derivative of the second plus second times the derivative of the first"
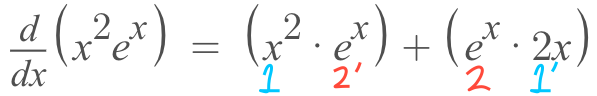
Quotient Rule
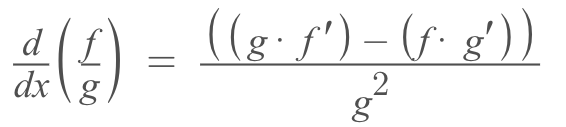
- Just like the product rule, this one's a little bit of a doozy and so my teacher taught us a song to help remember this (it's meant to go with the Snow White and the Seven Dwarfs HeIgh-Ho song): "You take the low, d hi, minus the high, d low, square the bottom and away we go, heigh-ho, heigh-ho!"

- This rule is more about identifying when you should use it and following the formula.
- With certain problems, especially since this is such a long process, you could change the denominator to a negative exponent (1/x = x^-1) and then use product rule
Want some more help on these rules, check out this video replay about the 🎥 Product and Quotient Rules.
Chain Rule
- Last but not least, we have chain rule. This is definitely the one that most people have the hardest time with so it's important that you can get the basics of it first.
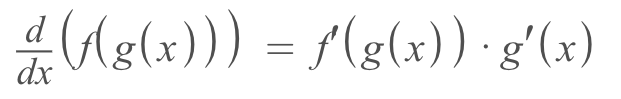
- This would sound something like "the derivative of f of g of x equals to the f prime of g of x times g prime of x"
- This is used when a function is composed of another one (kinda confusing, but it'll make sense)
- Say you have a problem like this:
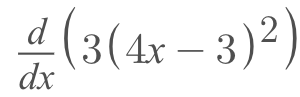
- First, we need to identify our inner and outer function. If we treat what's in the inner parentheses as one function and replace the whole with the variable 'x' for now.
- What we have now is
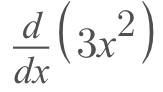
- We know how to take the derivative of this (power rule!) so we have the first part of this problem done
- Now, we have to take the derivative of the 'inside' part of the original function
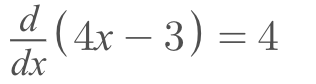
- The last step is to multiply these two parts together
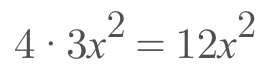
- And that's it! These were the basic rules for taking a derivative that you'll need to know in order to get that five! If you need some additional practice, check out the resources linked below!
📌 Practice with derivative rules!
- https://www.ixl.com/math/calculus/find-derivatives-of-polynomials
- https://www.khanacademy.org/math/in-in-grade-11-ncert/in-in-class11-derivatives/copy-of-derivative-basics-review-ab/e/derivatives-basics-challenge
- http://tutorial.math.lamar.edu/Problems/CalcI/DiffFormulas.aspx
- https://www.symbolab.com/practice/derivatives-practice
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.