8.11 Volume with Washer Method: Revolving Around the x- or y-Axis

Imagine the region we are revolving is bounded by y = f(x) on the top and y = g(x) on the bottom. Once we revolve the region around the axis, the cross sections will be a disc with a circle cut out from the middle. We call this the washer method because the cross sections look like hardware washers.  

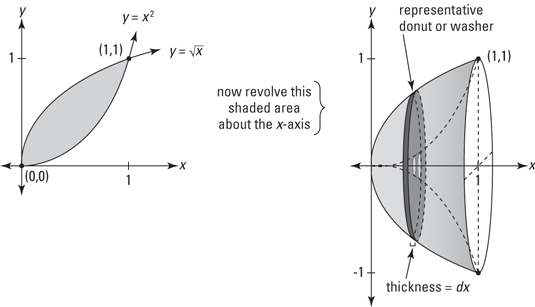
With the disc method, we need to find the radius of the disc in order to calculate the area of the cross section. With the washer method, we need to find the inner radius of the bottom function and the outer radius of the top function in order to find the area of the cross section. If you’re still confused, take a look at the example below. 

Suppose we have the region bounded by y = √x on top and y = x on the bottom. We are asked to find the volume of the figure if the region is revolved around the x-axis. 

The first step of this is to find inner and outer radii. The outer radius will be the top function, which is √x. The inner radius will be the bottom function, which is x. Now we can calculate the area of the cross section. This is as simple as subtracting the area of the smaller disc from the larger one. If the outer radius is √x and inner radius is x, then the area of the washer is π(√x)2 -  πx^2. This can be simplified to π(x - x^2). Now all we have to do is find the intersections of the functions to get the endpoints for the integral. To find the intersection, set the two functions equal to each other and solve for x. In this example, the intersections would be at x = 0 and x = 1. The final step is to integrate to find the volume: 

Generally, if you have a region whose area is bounded by the curve y = f(x) and the curve y = g(x) on the interval [a,b], the area of each washer will be 

Thus, the volume will be: 

Now, you try to use the formula with this example problem: 

If you rotate the region bounded by y = x + 2 and y = 2x about the x-axis and integrate it from x = 0 to x = 2, what is the volume of the resulting figure? 

Answer: 25.133

Solution: In this example, your functions are y = x + 2 and y = 2x: 

So, your f(x) = x - 2 and your g(x) = 2x. In this situation, it is important to note which function is on top and which is on the bottom. Now, all you have to do is integrate: