📚

All Subjects

🧲

AP Physics 2

💧

Unit 1

1.7 Conservation of Mass Flow Rate in Fluids

5 min read•june 18, 2024

Krish Gupta

Daniella Garcia-Loos

AP Physics 2 🧲

61 resources

See Units

Conservation of Mass Flow Rate in Fluids

The last major concept introduced in this unit is flow rate. While Bernoulli’s equation and Toricelli’s theorem from the last section remind us of the conservation of energy, the equations and concepts we learn in this section are based on the conservation of mass.

The flow rate (f), as defined above, is the flow speed of the liquid (v) times the cross sectional area (A) of the container. 🌊

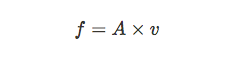
If we know the area at 2 points in a pipe and the velocity at one point, we can predict the velocity at the other point using the continuity equation.

Because the same amount of mass has to flow through the pipe in a time interval, flow rates at any 2 points have to be the same.

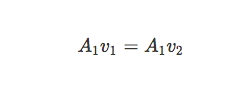
It is important to notice that this equation works best when the fluid is incompressible. The calculations, therefore, will be most accurate when dealing with fluids but will only provide approximations when working with gases.

Q. A point in a pipe, A, has a radius of X meters and a liquid velocity of 20 m/s. Another point, B, in the same pipe has a radius of 1.5X. Find the velocity of the liquid at point B.

A. We can always assume that the cross section area of a pipe is circular. Since area is correlated to radius by a factor of a square. That means if the radius is doubled the area will be quadruples and if the radius is tripled, the area will increase 9x fold.

Increasing the radius by 1.5 means we are increasing the area by (1.5)^2 = 2.25

Since the flow rate is constant, we have to decrease the velocity by a factor of 2.25 since the area increased by a factor of 2.25.

Therefore velocity at point B is

20/2.25 = 8.89m/s

The AP test won’t often ask you to calculate the flow rate, but it will ask you to compare the velocities at 2 different places in a pipe 💯. The part of the pipe with a bigger area will have smaller speed, and the part with the smaller area will have greater speed. Since velocity and pressure are related, we can relate pressure and area.

larger area = larger pressure = smaller velocity AND smaller area = smaller pressure = larger velocity

This relationship is the essence of these later key concepts ❤️.

Fluids tend to make up about 10% of the AP exam. The most commonly tested topics are the buoyant force, pressure, the relationship between area, pressure and velocity, and Bernoulli's equation.

Typically this unit is tested in conjunction with Unit 2: Thermal Physics, which we will learn next.

Here are some key things to know about the conservation of mass flow rate in fluids:

The conservation of mass flow rate states that the mass flow rate of a fluid through a system is constant, unless there is a gain or loss of mass within the system.
Mass flow rate is the rate at which mass flows through a system. It is equal to the mass of the fluid flowing through the system per unit time.
The conservation of mass flow rate can be expressed mathematically as:

Σṁin = Σṁout

Where Σṁin is the sum of the mass flow rates entering the system, and Σṁout is the sum of the mass flow rates leaving the system.

The conservation of mass flow rate is a fundamental principle of fluid mechanics and is often used to analyze and solve problems involving fluid flow.
The conservation of mass flow rate is closely related to the principle of continuity, which states that the mass flow rate through a system is equal to the product of the cross-sectional area of the system and the velocity of the fluid.

Example Problem #1:

A tank contains water at a temperature of 20°C. Water is pumped out of the tank at a rate of 2 kg/s, and an equal amount of water at a temperature of 40°C is pumped into the tank. The water in the tank is well-mixed, so the temperature of the water in the tank remains constant. What is the mass flow rate of the water leaving the tank?

Solution:

To solve this problem, we will use the conservation of mass flow rate to calculate the mass flow rate of the water leaving the tank.

According to the conservation of mass flow rate, the mass flow rate of the water entering the tank must be equal to the mass flow rate of the water leaving the tank.

The mass flow rate of the water entering the tank is 2 kg/s, and the mass flow rate of the water leaving the tank is unknown. We can set up the following equation:

2 kg/s = ṁout

Solving this equation, we find that the mass flow rate of the water leaving the tank is also 2 kg/s.

Therefore, the mass flow rate of the water leaving the tank is 2 kg/s.

Example Problem #2:

A pipe connects two tanks, Tank A and Tank B. Tank A contains water at a temperature of 20°C, and Tank B contains water at a temperature of 40°C. Water is flowing from Tank A to Tank B through the pipe at a rate of 2 kg/s. At the same time, water is being pumped out of Tank B at a rate of 3 kg/s, and an equal amount of water at a temperature of 20°C is being pumped into Tank B from a separate source. The water in Tank B is well-mixed, so the temperature of the water in Tank B remains constant. What is the mass flow rate of the water flowing from Tank A to Tank B through the pipe?

Solution:

To solve this problem, we will use the conservation of mass flow rate to calculate the mass flow rate of the water flowing from Tank A to Tank B through the pipe.

According to the conservation of mass flow rate, the mass flow rate of the water entering Tank B must be equal to the mass flow rate of the water leaving Tank B.

The mass flow rate of the water entering Tank B is 2 kg/s (the flow rate through the pipe from Tank A) plus 3 kg/s (the flow rate from the separate source), for a total of 5 kg/s. The mass flow rate of the water leaving Tank B is 3 kg/s (the flow rate being pumped out of Tank B). We can set up the following equation:

5 kg/s = 3 kg/s

Solving this equation, we find that the mass flow rate of the water flowing from Tank A to Tank B through the pipe is 2 kg/s.

Therefore, the mass flow rate of the water flowing from Tank A to Tank B through the pipe is 2 kg/s.

Browse Study Guides By Unit

💧Unit 1 – Fluids

1.1Fluid Systems

1.2Density

1.3Fluids: Pressure and Forces

1.4Fluids and Free-Body Diagrams

1.5Buoyancy

1.6Conservation of Energy in Fluid Flow

1.7Conservation of Mass Flow Rate in Fluids