📚

All Subjects

🧲

AP Physics 2

🔥

Unit 2

2.2 Pressure, Thermal Equilibrium, and the Ideal Gas Law

7 min read•june 18, 2024

Krish Gupta

Daniella Garcia-Loos

AP Physics 2 🧲

61 resources

See Units

Revisiting Pressure

We are already familiar with the idea of pressure. As we previously learned, pressure (P), measured in atmospheres (atms) or pascals (Pa), is the ratio between the force applied (F) and the surface area (A) of the object. A bigger force means a greater pressure, and a larger surface area means a smaller pressure. P=F/A In this unit, we shift our focus more towards gases instead of liquids like in the last unit. We will mostly spend our time looking at gases inside containers.

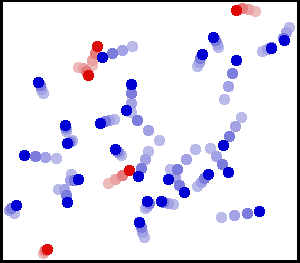
The image shows gas molecules inside a container in random motion. Notice how some molecules collide with the walls of the container and exert a force. Image Courtesy of WikiMedia.

So why is there pressure inside a container? Gas molecules are in constant random motion. Gas molecules collide with the container, exerting a force ✨ The force exerted over the surface area of the lid due to microscopic collisions leads to the overall macroscopic effect of pressure. The small picture leads to the big picture!

Temperature and Kinetic Energy 🥵

This section is vocabulary heavy, and we have to be very careful with the words we use and when we use them. Let’s get some basic definitions, and then we will connect them together.

Thermal energy is the energy due to increase in the temperature of the substance which leads to faster and more frequency collisions between gas atoms. The energy associated with the temperature rise and the faster molecules is what is known as thermal energy. Thermal energy is closely related to kinetic energy. You remember kinetic energy as the energy due to motion. Thermal energy is basically a form of kinetic energy.

The root mean square speed, commonly known as the RMS speed or velocity, is a measure of the average speed of the molecule. Both average kinetic energy and RMS speed can be best described using the Boltzmann distribution which you might be familiar with if you have taken a chemistry class before.

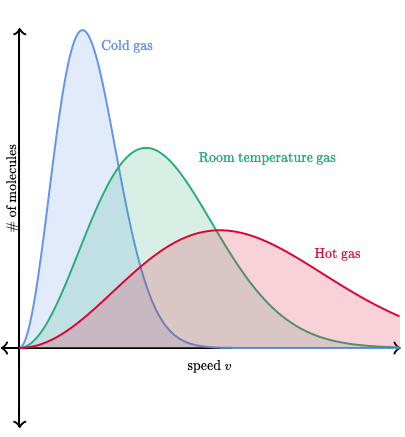
The image shows how increasing temperature leads to more molecules with higher speeds yet the peak of the distribution decreases. Image Courtesy of DeepAI.

As the temperature increases, there are more molecules with greater speed. Notice how the peak decreases since the spread of the distribution is increasing.

Temperature is a measure of an object’s internal energy. It tells us how much thermal energy an object has. We deal with temperature in everyday life. A lot of times we use the words temperature and heat interchangeably. However, in this unit temperature and heat mean quite different things.

Temperature is directly related to kinetic energy as described by the equation below. The two are linked by the Boltzmann constant (1.38x10^-23 J/K)

Heat is how much thermal energy is transferred from one object to another. It measures the amount of energy transmitted. Thermal energy is transferred from the hotter object to the colder object until thermal equilibrium is reached.

Thermal equilibrium and transfer of heat is something you have seen and experienced before. These factors control why ice melts in a room, why car seats heat up, or why a cold shower doesn’t feel so cold after a few minutes.

If two objects are in thermal equilibrium, they will have the same temperature and, therefore, no net flow of heat. It is important to truly understand what equilibrium means: when two objects are in thermal equilibrium they still have molecules colliding and transferring energy to each other on a small scale, but there is no overall or net transfer of heat.

Temperature is a property of an object. Heat is a property associated with interaction between two objects. While they may seem similar, it is important for you to know the precise distinctions between these concepts.

Heat and temperature are related but distinct physical quantities that describe the energy of a system. Here are the key differences between heat and temperature:

Heat is a form of energy that is transferred from one body to another as a result of a difference in temperature. It is measured in units of energy, such as joules or calories.
Temperature is a measure of the average kinetic energy of the particles in a body. It is measured in units of temperature, such as degrees Celsius or Fahrenheit.
Heat is a flow of energy from a body with a higher temperature to a body with a lower temperature.
Temperature is a measure of the average kinetic energy of the particles in a body, regardless of the amount of heat being transferred.
Heat can be transferred by conduction, convection, or radiation.
Temperature can be measured using a thermometer.

The Ideal Gas Law

This law needs no introduction If you have taken any science class before, you are very familiar with the Ideal Gas Law. It is at the heart of engineering and is used by scientists around the world all the time. In any case, we review this famous law and see the reasoning behind it along with its limitations.

Charles' Law states that as volume goes up, temperature goes up.

Gay-Lussac’s Law states that as pressure goes up, temperature goes up.

Avogadro's Law says as the number of moles of a gas goes up, the volume goes up. All these laws show a direct correlation

Boyle’s Law states that as volume goes up, pressure goes down and vice versa. This is an example of an indirect correlation.

Also, note that all these relationships are linear. That means if one thing doubles, the other thing also increases or decreases by a factor of 2.

The Ideal Gas Law essentially combines the 4 laws above. So if you know this ONE formula, you basically know all the information in that long, wordy and boring paragraph above. This formula relates the pressure inside a container (P), the containers volume (V), the temperature in the container (T) and the number of moles of the gas in the container (n) and the perfect key that fits all these pieces together and solves the puzzle is the universal gas constant, R.

As you can see, this equation describes all of the relationships we talked about earlier. It accounts for everything.

However, this equation is not perfect. It only works if we have an ideal gas. I mean...it's in the name! Gases display ideal behavior at high temperatures and low pressures 💨

So, the Ideal Gas Law overlooks some things.

Firstly, the molecules themselves take up space, but we ignore that.
Secondly, there are intermolecular forces between the molecules that might affect the pressure but we don't count for those either.
Also, we assume that all collisions are elastic, meaning no kinetic energy is lost when two molecules bump into each other.

These assumptions are fairly reasonable and work best if we are dealing with high temperatures and low pressures.

There is another version of the Ideal Gas Law that is more useful when dealing with small quantities. In this equation, we use the number of molecules of gas instead of moles and we utilize the Boltzmann constant.

For the AP exam, you are free to use the Ideal Gas Law since it's so important‼️ But it is noteworthy to mention the deviations and assumptions we make with this law. Not all real gases behave like ideal gases, and these factors might affect the calculations slightly in a laboratory.

The Van der Waals equation accounts for these factors. However, Van der Waals equation has never been tested on any of the AP Physics exam so we won't expand on it. But, it's good to know it exists for higher-level physics courses 🤓

The ideal gas law is a mathematical relationship that describes the behavior of gases under certain conditions. Here are some key things to know about the ideal gas law:

The ideal gas law is a combination of three other laws that describe the behavior of gases: the ideal gas law, Boyle's law, and Charles' law.
The ideal gas law states that the pressure of a gas is directly proportional to its temperature and inversely proportional to its volume, provided that the number of gas molecules and the mass of the gas are held constant.
The ideal gas law can be written as PV = nRT, where P is the pressure of the gas, V is the volume of the gas, n is the number of gas molecules, R is the ideal gas constant, and T is the temperature of the gas.
The ideal gas law is only applicable to gases that are ideal, meaning that they are perfect gases that do not interact with each other and do not take up any space.
The ideal gas law can be used to predict the behavior of gases under different conditions, such as how the volume of a gas will change as the temperature changes or how the pressure of a gas will change as the volume changes.

Browse Study Guides By Unit

💧Unit 1 – Fluids

🔥Unit 2 – Thermodynamics

2.0Unit 2 Overview: Thermodynamics

2.1Thermodynamic Systems

2.2Pressure, Thermal Equilibrium, and the Ideal Gas Law

2.3Thermodynamics and Forces

2.4Thermodynamics and Free-Body Diagrams

2.5Thermodynamics and Contact Forces

2.6Heat and Energy Transfer

2.7Internal Energy and Energy Transfer

2.8Thermodynamics and Elastic Collisions: Conservation of Momentum