Daniella Garcia-Loos
S
Saarah Hasan
AP Physics 2 🧲
61 resourcesSee Units
What is a wave? Well, in simple terms, a wave can be described as a disturbance that carries energy through a medium—the substance/material that carries the wave—from one place to another. Waves transfer energy without transferring matter; energy moves from place to place, yet the particles of matter in the medium return to their original location.
Let’s take a look at this in a real-life example.
Imagine a stadium wave. Each person in the audience stands up and then quickly sits back down to make the wave. The disturbance travels through the stadium, but the people in the audience don’t move from where their seat is. They don’t walk around the stadium to make the wave.
Properties of Waves
While all waves share some basic properties, they can come in different shapes and forms. It’s common to categorize waves based on certain characteristics:
- Transverse Wave—A wave in which particles of the medium move in a direction perpendicular to the motion of the wave.
- Longitudinal Wave—A wave in which particles of the medium move parallel to the motion of the wave.
- Mechanical Wave—A wave that isn’t capable of transmitting its energy through a vacuum; mechanical waves require a medium to travel and can be both longitudinal or transverse.
- Electromagnetic Wave—A wave that’s capable of transmitting its energy through a vacuum; electromagnetic waves are produced by the vibrations of charged particles and are always transverse.
Longitudinal vs Transverse Waves
Longitudinal waves are waves in which the disturbance travels in the same direction as the wave itself. These waves involve a compressional motion, in which the particles of the medium move back and forth along the direction of the wave.
Transverse waves are waves in which the disturbance travels perpendicular to the direction of the wave itself. These waves involve a lateral motion, in which the particles of the medium move up and down or side to side in a direction that is perpendicular to the direction of the wave.
An example of a longitudinal wave is a sound wave, which travels through the air as a series of compressions and rarefactions. An example of a transverse wave is a water wave, which travels through a body of water as a series of crests and troughs.
Mechanical vs Electromagnetic Waves
Mechanical waves are waves that require a medium, or a physical substance, to propagate through. Examples of mechanical waves include sound waves, which require a medium such as air or water to travel through, and surface waves, which require a solid surface such as the ground or the surface of a lake.
Electromagnetic waves are waves that do not require a medium to propagate through. They can travel through empty space, as well as through various materials such as air, water, or metal. Examples of electromagnetic waves include light, radio waves, and X-rays.
The main difference between mechanical and electromagnetic waves is the way in which they transfer energy. Mechanical waves transfer energy through the movement of particles in the medium, while electromagnetic waves transfer energy through the oscillation of electric and magnetic fields.
Anatomy of Waves
Let’s take a closer look at the parts of waves.🔎
Transverse Waves:
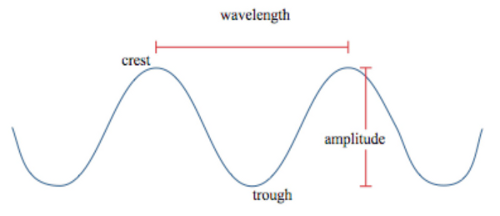
Taken from Wikimedia Commons
Longitudinal Waves:
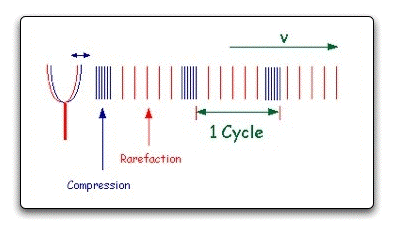
Taken from Wikimedia Commons
- Wavelength (λ)—The distance/length of the wave measured from two identical points, from crest to crest or from trough to trough; it’s the length of one complete wave cycle.
- Amplitude (a)—The height of the wave or distance from rest to max. displacement. Amplitude is proportional to the amount of energy carried by a wave: a high energy wave has a high amplitude; a low energy wave has a low wave.
- Crest—The point on a wave where the amount of positive/upward displacement from rest is at a max.
- Trough—The point on a wave where the amount of negative/downward displacement from rest is at a max.
- Compression—A region in a longitudinal wave where the particles are closest together (max. density).
- Rarefaction—A region in a longitudinal wave where the particles are farthest apart (min. density).
- Frequency (f)—The number of waves made per second; measured in Hertz (Hz)
- Period (T)—The amount of time it takes to make one wave; measured in seconds (s).
Polarization is the property of a wave that describes the direction of its vibration. In a polarized wave, the vibration of the particles in the medium is oriented in a specific direction, rather than being randomly oriented. Polarization is an important property of waves because it determines how the wave will interact with certain materials and how it will be absorbed or reflected by those materials.
Wave Equations
👇Let’s jot down the formulas/equations we’ll need to solve wave-related physics problems.👇
T=1/f f=1/T
The frequency is the reciprocal of the period and vice versa.
speed=distance/time
For waves, the speed is the distance traveled by a point (like the crest/trough) on the wave over a given amount of time. In the time of one period, a wave moves the distance of one wavelength. So from that, we can say:
Speed=Wavelength/Period ➡️ v=λ/Tv=λ/T
Speed=Wavelength*Frequency ➡️ v=λ*fv=λ∗f
While wave speed is calculated by multiplying frequency and wavelength, changing either of the two doesn’t affect wave speed. The speed of a wave depends upon the medium in which the wave travels.
Check out this interactive to explore this concept further.
Let's walk through an example problem:
You are given a graph of the displacement of a mechanical wave as it travels through a medium. The wave is shown as a function of time (t) and distance (x). The wave is propagating in the positive x direction.
Your task is to:
- Analyze the graph to determine whether the wave is polarized.
- If the wave is polarized, identify the direction of polarization.
- Explain why the wave must have a vibration perpendicular to the direction of energy propagation.
Solution:
- To determine whether the wave is polarized, we need to look at the shape of the waveform in the graph. If the waveform is symmetrical about a central axis, then the wave is unpolarized. If the waveform is asymmetrical and has a specific orientation, then the wave is polarized.
In this case, the waveform appears to be asymmetrical and oriented in a specific direction, so we can conclude that the wave is polarized.
2. To identify the direction of polarization, we need to look at the orientation of the waveform. If the waveform is oriented along the x-axis, then the wave is horizontally polarized. If the waveform is oriented along the y-axis, then the wave is vertically polarized.
In this case, the waveform appears to be oriented along the y-axis, so we can conclude that the wave is vertically polarized.
3. To explain why the wave must have a vibration perpendicular to the direction of energy propagation, we can use the concept of polarization. Polarization refers to the direction of the vibration of the wave. In a vertically polarized wave, the vibration is perpendicular to the direction of energy propagation. This means that the energy of the wave is being transmitted primarily in the x direction, while the vibration of the particles in the medium is occurring in the y direction.
This is why a polarized wave must have a vibration perpendicular to the direction of energy propagation. The energy of the wave is transmitted in one direction, while the vibration of the particles in the medium is occurring in a different direction.
Practice Problems:🧩
1. Which of the following statements about the speed of waves on a string are true?
I. The speed depends on the tension in the string
II. The speed depends on the frequency
III. The speed depends on the mass per unit length of the string.
A) II only
B) I and II only
C) I and III only
D) II and III only
E) I, II and III
2. A wave has a frequency of 50 Hz. The period of the wave is:
A) 0.010 s
B) 0.20 s
C) 7 s
D) 20 s
E) 0.020 s
3. If the frequency of sound is doubled, the wavelength:
A) halves and the speed remains unchanged
B) doubles and the speed remains unchanged
C) is unchanged and the speed doubles
D) is unchanged and the speed halves
E) halves and the speed halves
4. An observer hears a sound with a frequency of 400 Hz. Its wavelength is approximately:
A) 0.85 m
B) 1.2 m
C) 2.75 m
D) 13.6 m
E) 44 m
5. As sound travels from steel into air, both its speed and its:
A) wavelength increase
B) wavelength decrease
C) frequency increase
D) frequency decrease
E) frequency remain unchanged
Answers:
- C: Based on the formula
- E: Use T = 1/f
- A: Frequency and wavelength are inverse
- A: Speed of sound is 340, use v = f λ
- B: When sound travels into less dense medium, its speed decreases (unlike light) … however, like all waves when traveling between two mediums, the frequency remains constant. Based on v = f λ, if the speed decreases and the frequency is constant then the λ must decrease also.
Browse Study Guides By Unit
💧Unit 1 – Fluids
🔥Unit 2 – Thermodynamics
⚡️Unit 3 – Electric Force, Field, & Potential
💡Unit 4 – Electric Circuits
🧲Unit 5 – Magnetism & Electromagnetic Induction
🔍Unit 6 – Geometric & Physical Optics
⚛️Unit 7 – Quantum, Atomic, & Nuclear Physics
📆Big Reviews: Finals & Exam Prep
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.