📚

All Subjects

⚙️

AP Physics C: Mech

🚗

Unit 1

1.2 Kinematics: Motion in Two Dimensions

5 min read•june 18, 2024

Gerardo Rafael Bote

Daniella Garcia-Loos

AP Physics C: Mechanics ⚙️

68 resources

See Units

Kinematics: Motion in 2-D

Great! You know how to consider motion in 1 dimension! Is your brain ready to handle TWO dimensions?

This is where projectile motion usually comes in.

Projectile motion refers to the motion of an object that is projected into the air and then is subject to the force of gravity.

The path that the projectile follows is called its trajectory.

The projectile's motion can be described by a set of parametric equations that give the projectile's position in terms of time: x(t) and y(t).

The initial velocity of the projectile, v0, determines the shape of the projectile's trajectory.

The acceleration of the projectile due to gravity is a constant, -g. This means that the velocity of the projectile in the y direction (vy) is constantly changing at a rate of -g.

Using calculus, we can find the velocity and acceleration of the projectile at any time t by taking the first and second derivatives of the position equations.

We can also use calculus to find the maximum height reached by the projectile and the time it takes for the projectile to reach this maximum height.

The range of the projectile (the horizontal distance it travels) can be found by setting the y coordinate of the projectile to 0 and solving for the time t.

Take a look at the picture below:

Image from DKPhysics

There are now two components to each velocity: the horizontal velocity and vertical velocity. The only component being affected by gravity (g=9.81 m/s2 ≈ 10m/s2) is vertical velocity. Therefore, an object's horizontal velocity does not change until the final impact.

An object's horizontal components and vertical components are independent of each other; however, they are related to each other via TIME.

When the object reaches its max height, be aware that v_y = 0

Look at how each of the horizontal and vertical components are comprised:

X-Direction Components

Y-Direction Components

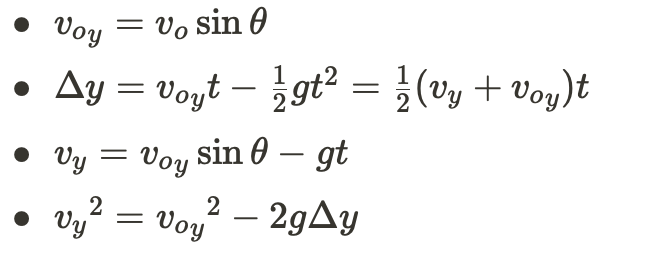
⚠️WOAH... How did you get all of those equations above? Are they on the formula sheet?

First of all, thanks for mentioning the formula sheet! It is useful when you need to derive an equation, like what you see above! You will see this sheet when you take the AP exam in May.

Image from collegeboard.org

For this unit, the first three equations (in red box) are emphasized in finding missing values, whether it be velocity, acceleration, or time. The first three equations can also be modified to fit either the y-direction or x-direction as well! Also remember that some values may be equal to 0, canceling out some adding or subtracting.

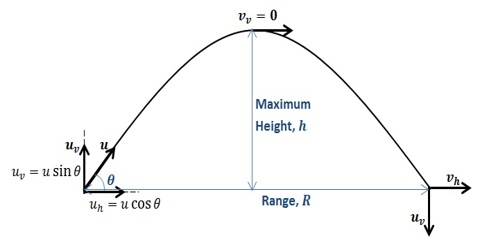
Image from QS Study

For example, let's use the first equation above (v_x = v_x0 + a_y t )to be modified in the y-direction and solve for the time it takes a projectile to reach its max height:

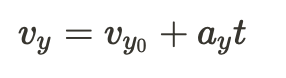
There are many values we can put in to solve for the time it takes a projectile to reach its max height

(t). First, let's assume the following: the ball above starts at rest on the ground. Then, the ball is launched at an angle of θ. From the following info, you know that at max height, the vertical velocity of an object is 0. You also know that a _y =−g because there is always a downward acceleration due to gravity. Lastly, you know that v_{y_0} = v_osinθ because of how trigonometry works within a projectile's launch. You then set up the equation and evaluate:

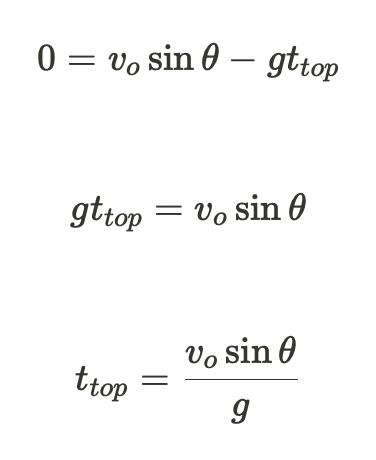
You might be confused on how projectile motion still works, so try out the PhET Simulation below to experiment with different factors of projectile motion (i.e., time, velocity, acceleration)!

You can also see why AP says that you can assume "air resistance is negligible." 😅

Here are some tips for using calculus to analyze 2D kinematics problems:

Use position-time graphs to visualize the motion and make it easier to understand the problem.
Use the slope of the position-time graph to find the velocity at any point in time.
Use the velocity-time graph to find the acceleration at any point in time.
Use the equations of motion (such as x(t) = x0 + v0t + 1/2at^2) to find position, velocity, or acceleration at any time, given initial conditions.
Remember that displacement is the change in position, and average velocity is the total displacement divided by the time interval.
Use integration to find displacement and average velocity, given a velocity function.
Use the Fundamental Theorem of Calculus to relate the velocity function to the position function.
Don't forget to consider the direction of motion when analyzing the problem!

Kinematics Practice Questions:

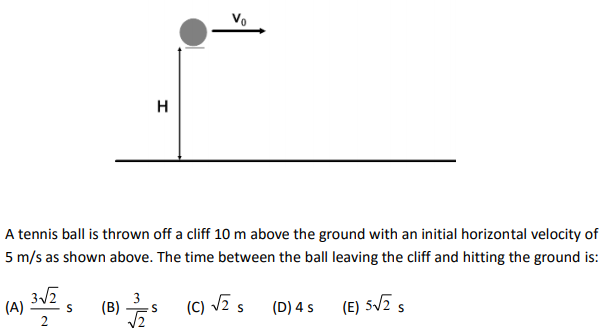
Image from New Jersey Center for Teaching & Learning

Answer

The correct answer is C. For this problem, all you need to know is the vertical components of the motion since we do not need to know the horizontal range of the tennis ball. We can use the

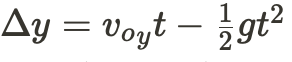
equation since we know everything in the equation but time.

⚠️Wait... what is the value of v_oy

The value of v_oy is 0 because there is no initial vertical velocity. Therefore, you can just cancel out v_oy t part, leaving Δy=1/2 gt^2 This is how you set up the equation:

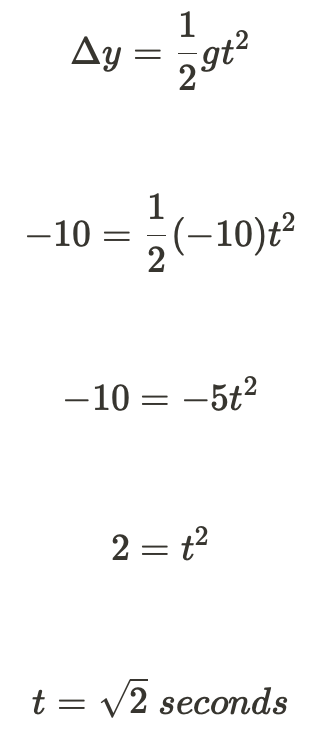
Image from collegeboard.org

Answer

The correct answer is C. The only accceleration that takes place in projectile motion is the downward acceleration of gravity (-9.8 m/s^2). A is wrong because the vertical component of the sphere's velocity is actually at a minimum(0) at point P. B is wrong because the horizontal component of the sphere's velocity is constant throughout the whole motion, not at just point P. D is wrong because the sphere's speed is not constant throughout the whole motion, especially at point P. E is wrong because the displacement changed according to the sphere's starting point (i.e., origin).

Image from New Jersey Center for Teaching & Learningg

Answer

The correct answer is A. To calculate the horizontal and vertical components of a projectile launched at an angle, you need to consider the trigonometry behind the ball's launch. You should know that

Then calculate:

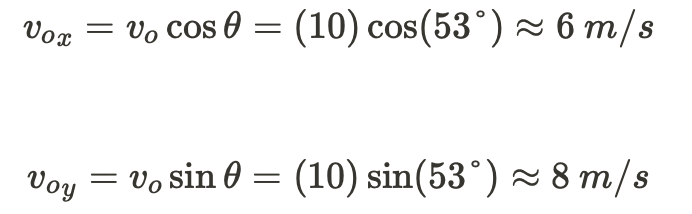
TIP: Be careful when the problem specifies whether you should be in degrees or radians!

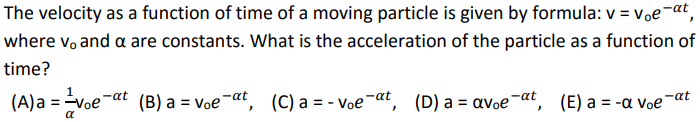
Answer

The correct answer is E. To solve this question correctly, you need to know that the acceleration function is the derivative of the velocity function. Then, you need to know proper derivative rules to correctly get E. This is the derivative rule for functions with e, Euler's number (let u represent any real function):

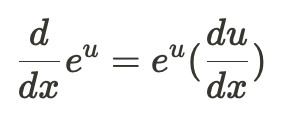
In this case, you also need to know that constants multiplied by e^u or other exponential functions stay since it is not related to x. Therefore, the constant v_o stays since it represents a number. du/dx means to derive the function represented by u, and deriving −αt would give us −α.

Browse Study Guides By Unit

🚗Unit 1 – Kinematics

1.0Unit 1 Overview: Kinematics

1.1Kinematics Overview and Motion in One Dimension

1.2Kinematics: Motion in Two Dimensions

🚀Unit 2 – Newton’s Laws of Motion

🎢Unit 3 – Work, Energy, & Power

🎳Unit 4 – Systems of Particles & Linear Momentum

🚲Unit 5 – Rotation

🌊Unit 6 – Oscillations

🪐Unit 7 – Gravitation

📚Study Tools