5.1 Torque and Rotational Statics
5 min read•june 18, 2024
Daniella Garcia-Loos
AP Physics C: Mechanics ⚙️
68 resourcesSee Units
Torque & Rotational Statics
Torque is the rotational analog of force, which is what causes an object to rotate around its center of mass. It's units are (kgm^2)/(s^2)or N*m.
Torque(T) is the cross product of the radius(r) and the force(F) applied at that radius, which in equation form is:
In which r, F, and T are vectors!
Here's an image of an application of torque:
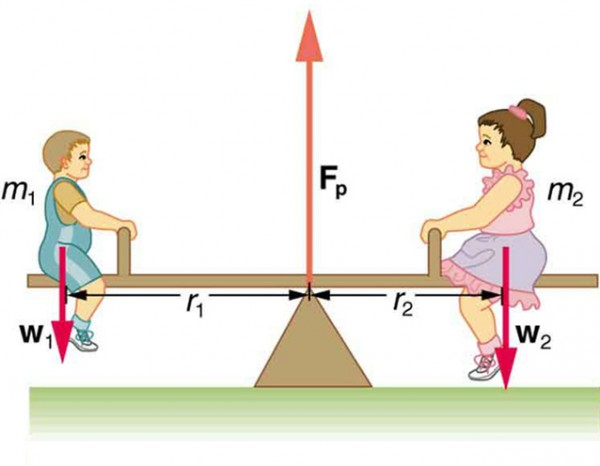
Taken from Lumen Learning
First Condition of Equilibrium: This condition is about static and dynamic equilibrium in which the object either has a 0 or constant velocity and the acceleration is 0, meaning the net force is zero.
Second Condition of Equilibrium: This condition states that the sum of the net torques is 0 and the angular acceleration is 0.
Both of these conditions must be satisfied in order for an object/system to be in equilibrium!
Here are some key things to remember about torque and rotational statics:
- Torque is a measure of the rotational force applied to an object. It is defined as the product of the force applied to an object and the lever arm (the distance from the point of application of the force to the axis of rotation).
- Torque is a vector quantity, with both magnitude and direction. The direction of the torque is perpendicular to the plane defined by the force and the lever arm.
- Torque is measured in newton-meters (N*m).
- The net torque acting on an object is the sum of all the torques acting on the object. The net torque determines the rotational acceleration of the object.
- Rotational statics is the study of objects that are in rotational equilibrium. This means that the net torque acting on the object is zero, and the object is not accelerating.
- To achieve rotational equilibrium, the torques acting on an object must balance out. This means that the clockwise torques must equal the counterclockwise torques.
- In rotational equilibrium, the sum of the forces acting on an object is not necessarily zero. The forces can still be in balance even if the torques are not.
Moment of Inertia
Rotational Inertia(I) or Moment of Inertia is essentially an object's resistance to changes in its rotation. It is essentially the sum of all the tiny points of mass times the radius(r) squared of an object, in which the calculus definition for it is:
However, these derivations typically take a very long time and require a strong level of comfort in calculus, so AP doesn't usually make students derive them. Most of the time they will use one that is very common, like a rod, or they will give it to you in the question.
Here are some examples of the most commonly seen ones, take a look at the axis of rotation too!
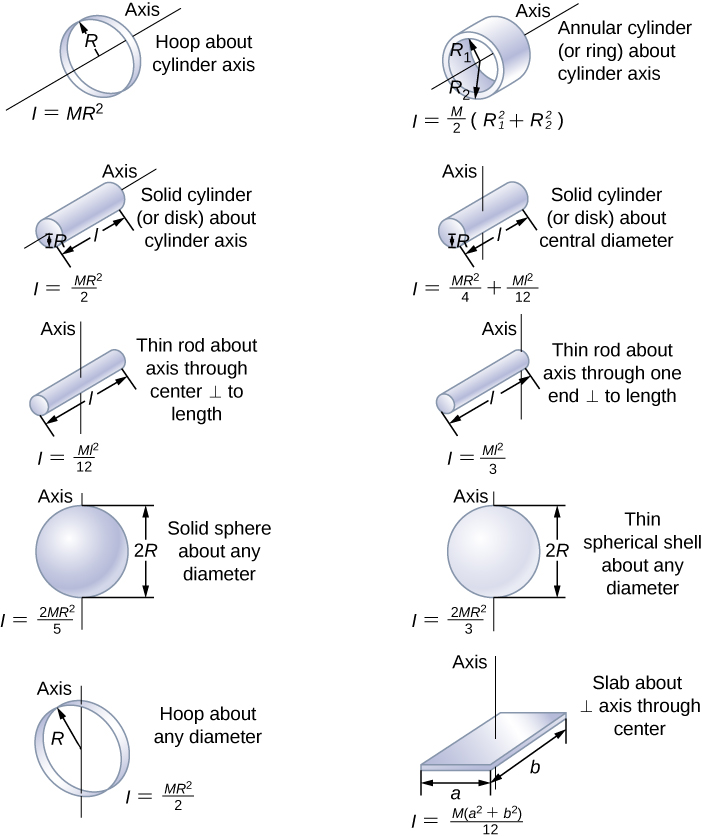
Taken from OpenStax
Here are some key things to remember about rotational inertia:
- Rotational inertia, also known as moment of inertia, is a measure of an object's resistance to rotational acceleration. It is a scalar quantity that depends on the mass of the object and the distribution of the mass around the axis of rotation.
- The greater an object's moment of inertia, the more difficult it is to accelerate the object.
- The moment of inertia of an object depends on the shape of the object and the location of the axis of rotation.
- For a solid object with a uniform mass distribution, the moment of inertia is equal to the object's mass times the square of the distance from the axis of rotation to the object's center of mass.
Sometimes, the axis of rotation isn't perfectly where we want it to be: at the center of mass. So we employ an awesome trick called parallel axis theorem!
In which I(new) is the rotational inertia of the object with the shifted axis, I(com) is the rotational inertia of the object with the axis at the center of mass (like the image above), m is mass, and h is the shift of the axis in meters.
Here is a step-by-step guide on how to apply the parallel axis theorem:
- Identify the object or system that you want to analyze. This is the object or system for which you want to calculate the moment of inertia.
- Draw a simple sketch of the object or system. You should include all relevant features of the object or system, such as its shape, size, and orientation.
- Identify the axis of rotation. This is the line around which the object or system will rotate.
- Identify the center of mass of the object or system. This is the point at which the mass of the object or system is evenly distributed.
- Choose a reference point on the axis of rotation. This is the point where you want to calculate the moment of inertia.
- Calculate the distance between the center of mass and the reference point. This is the distance r.
- Calculate the moment of inertia of the object or system about its own center of mass using the appropriate formula for the shape of the object or system. This is the moment of inertia I_cm.
- Use the parallel axis theorem to calculate the moment of inertia about the reference point: I = I_cm + M * r^2
Where I is the moment of inertia about the reference point, I_cm is the moment of inertia about the center of mass, M is the mass of the object or system, and r is the distance between the center of mass and the reference point.
Practice Questions
1) Two children push on opposite sides of a door during play. Both push horizontally and perpendicular to the door. One child pushes with a force of 17.5 N at a distance of 0.600 m from the hinges, and the second child pushes at a distance of 0.450 m. What force must the second child exert to keep the door from moving? Assume friction is negligible. (Taken from Lumen Learning)
Answer:
2)

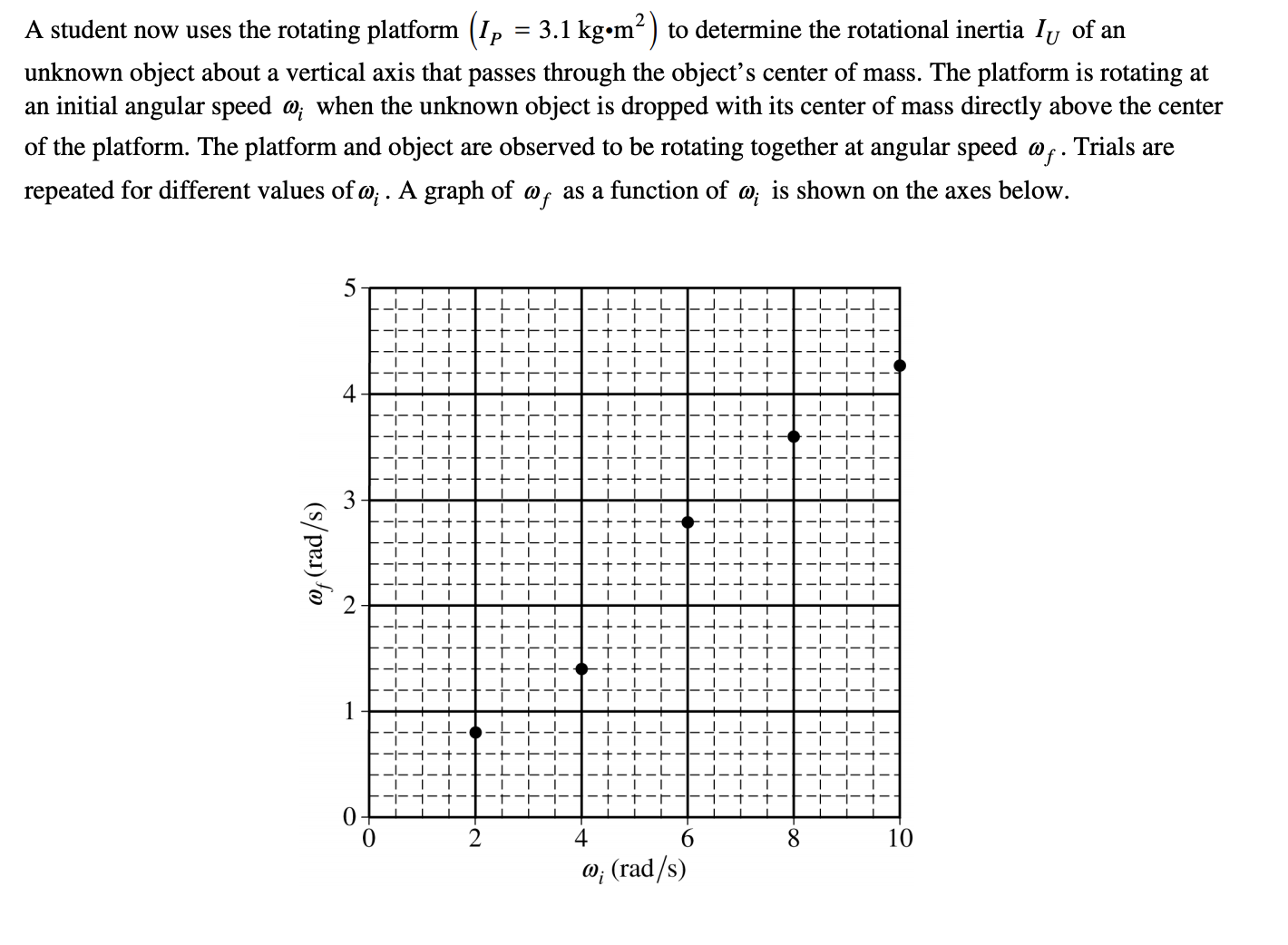
Taken from College Board

Answer:
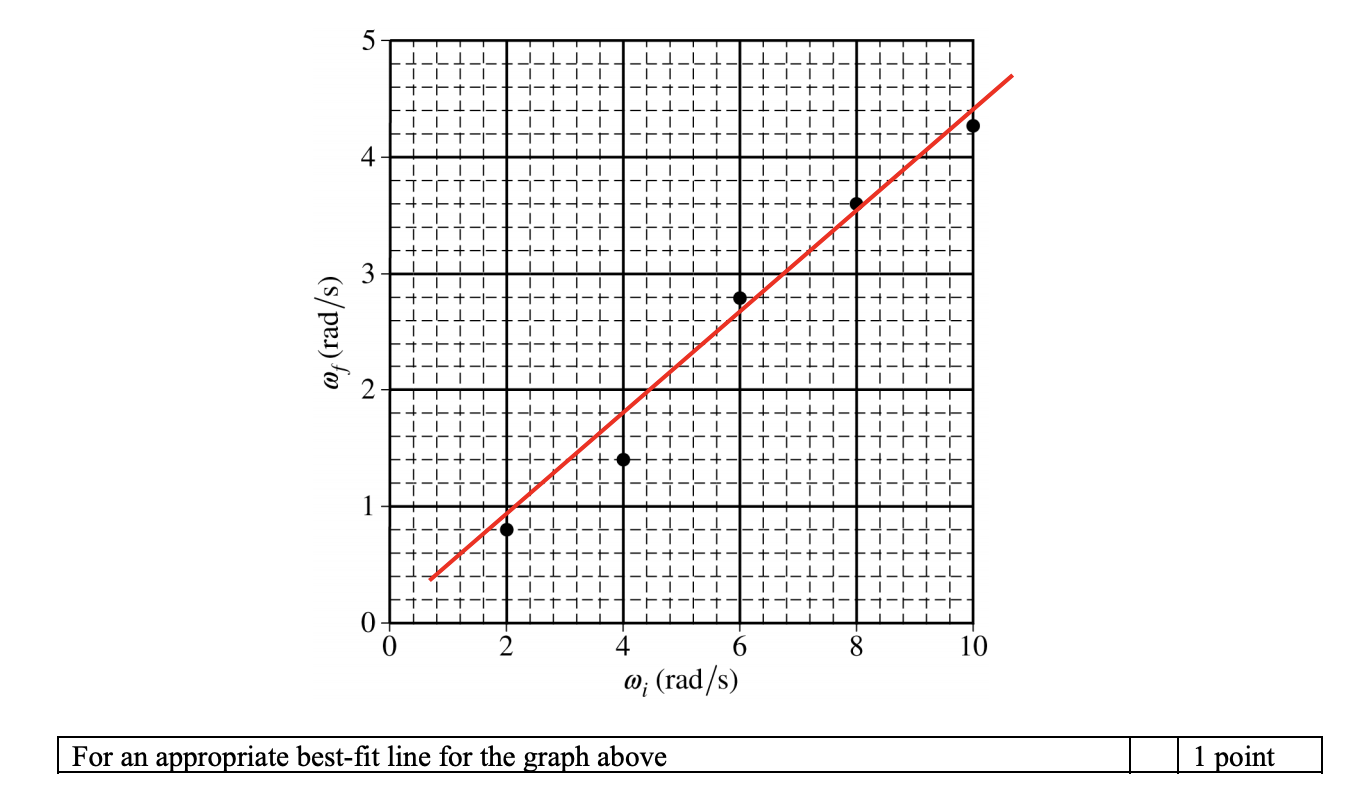
3)

Answer:

Browse Study Guides By Unit
🚗Unit 1 – Kinematics
🚀Unit 2 – Newton’s Laws of Motion
🎢Unit 3 – Work, Energy, & Power
🎳Unit 4 – Systems of Particles & Linear Momentum
🚲Unit 5 – Rotation
🌊Unit 6 – Oscillations
🪐Unit 7 – Gravitation
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.