Peter Apps
AP Physics C: E&M 💡
26 resourcesSee Units
What the Flux?!?
Flux is a very useful concept to help describe a wide variety of physics concepts. We're going to apply it here for electric fields, and then use it to help describe magnetic fields. Basically flux describes how much of something goes through a given area.
We're going to imagine an area on the surface of a charged object. It doesn't matter what the object is. The electric flux is then described by how many electric field lines pass through the area. Generally, we define the area to be parallel to the electric field, since this simplifies the math. However, if we can't do that, we take the dot product between the area vector and the electric field to determine the flux.
Let's look at the total flux in this image below.
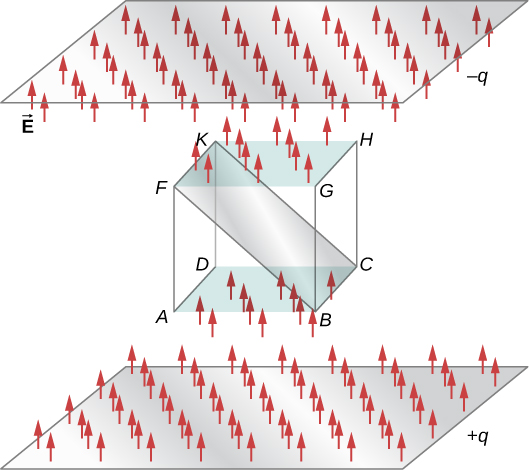
Image from opentextbookbc.ca
When field lines enter a closed surface, the flux is negative. When they exit the surface, the flux is positive.
In this case, we see that there are 11 field lines entering the area ABCD and 11 field lines exiting FGHK. The flux from these two areas cancel out, and, therefore, the total flux is 0. A simple way to think about this is that if there isn't a source of charge or a sink (something that absorbs charge) **inside the area, the net flux is 0.
Gauss' Law
Gauss's Law relates the flux on a closed surface to the amount of charge enclosed by the surface.
Let's break this formula down a bit and see where it comes from.
Let's try to find the flux. Remember that E is constant across the entirety of the surface. Adding up all the partial areas of the sphere gives us the surface area. (A= 4*pi*r^2).
In short, Gauss's Law states that sum of the charge sources within a closed surface is equal to the total electric flux through the surface. It's important to note that when we define a Gaussian Surface, especially on an AP Exam FRQ section, that we choose a 3-D shape (like pill-box or sphere) and not a 2-D shape like a circle. Many students lose an easy point on an FRQ section each and every year (as almost every year sees a charge distribution FRQ on the exam), so don't let that be you!
When drawing Gaussian Surfaces, the size of that surface is indepdent of the amount of flux through the surface. However, the enclosed charge and total flux are the two values proportional to one another in Gauss' Law, so make sure that your Gaussian Shape that you draw/choose encloses the charge described fully.
Density in Gauss' Law
When dealing with complicated Gauss' Law problems (in FRQ and MCQ sections of the AP Exam), sometimes we only have a portion of the total Q as q_enc. However, we can usually find the value for q_enc if we have an evenly distributed charge density (meaning that 1/2 of the total volume encloses 1/2 of the total charge) easily. Sometimes, it's harder (but still doable🤧) if we're given a density rho (ρ) as a function of radius. The charge enclosed for those problems can be calculated as an integral of ρ(r)*dV.
Practice Problems
1.
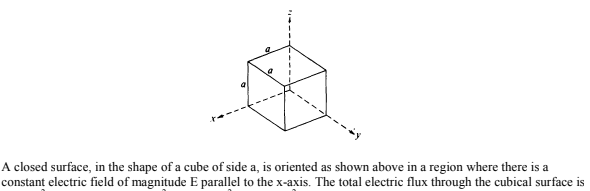
Image from AP Classroom
There is no electric flux in the cube. Therefore there is also no enclosed charge in the cube by Gauss' Law equation.
2.
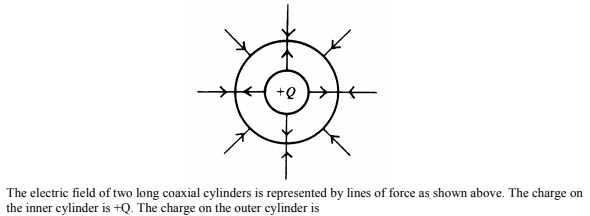
Image from AP Classroom
We know there is +Q enclosed in the inner cylinder. We can see 4 lines of flux leaving that cylinder. With the larger cylinder, there are 8 lines entering the cylinder. This means that the net charge enclosed by the larger cylinder is -2Q. So the outer cylinder must have a charge of -3Q.
3.

Image from AP Classroom
The left side of the equation for Gauss' Law (below) is pretty straightforward). We're given a sphere, so the integral simplifies to the surface area of the sphere: E(4πr^2)
The right side is a bit more complicated. Our surafce is inside the sphere, so we don't enclose the full charge Q. Instead, we enclose some fraction of Q. The fraction is directly related to the volume of our surface's sphere: q_enc = Qr^3/R^3. We can make this assumption because the charge is evenly distributed.
Therefore, when we put both sides of the Gauss' Law equation together, we choose (D).

Image from AP Classroom
The sphere is conducting, so any fields outside it can't penetrate inside and don't influence the internal field. The only charge enclosed is +Q, so choice A is the correct answer.
Practice FRQ
The FRQ below is very similar to one that could likely be on your AP exam. Tehcnically, you have learned all of the skills to successfully complete this FRQ, but it might be easier once you read the study guide for section 1.5, so make sure to check that out if you need a quick refresher!
(courtesy of the 2003 AP Physics C: Electricity + Magnetism Free Response section, question 1)
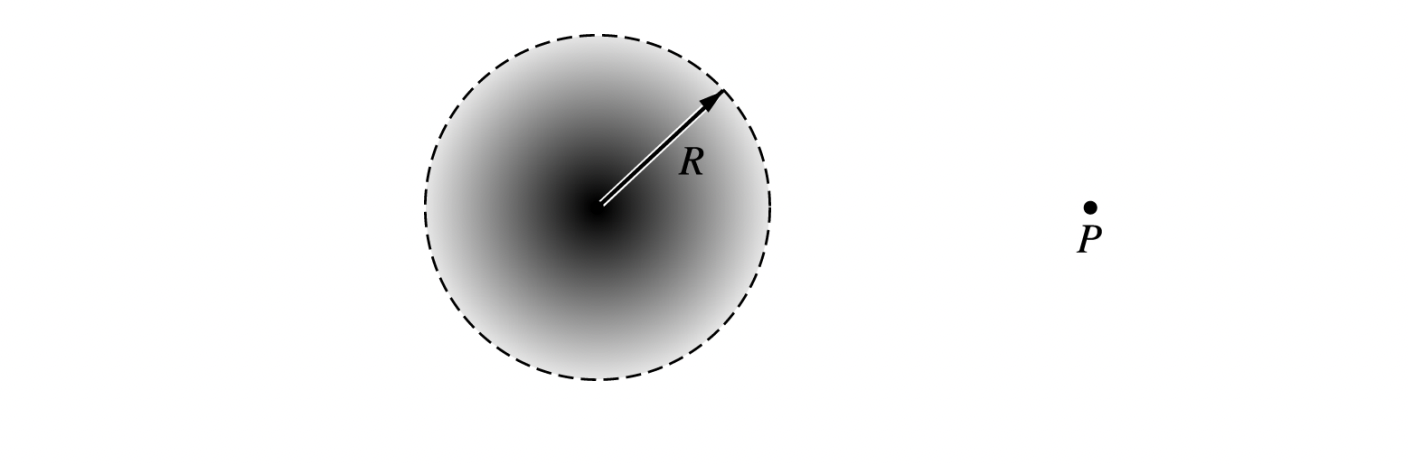
A spherical cloud of charge of radius R contains a total charge +Q with a nonuniform volume charge density that varies according to the equation
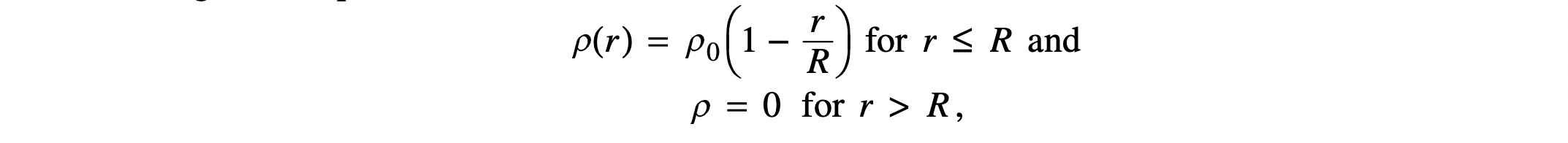
where r is the distance from the center of the cloud. Express all algebraic answers in terms of Q, R, and fundamental constants.
(a) Determine the following as a function of r for r > R .
i. The magnitude E of the electric field
ii. The electric potential V
(b) A proton is placed at point P shown above and released. Describe its motion for a long time after its release.
(c) An electron of charge magnitude e is now placed at point P, which is a distance r from the center of the sphere, and released. Determine the kinetic energy of the electron as a function of r as it strikes the cloud.
(d) Derive an expression for ρ0 (rho naught).
(e) Determine the magnitude E of the electric field as a function of r for r <= R .
Answer/Scoring Guidelines
The scoring guidelines are located at this PDF on the CollegeBoard website for Question #1.
Browse Study Guides By Unit
⚡️Unit 1 – Electrostatics
🔋Unit 2 – Conductors, Capacitors, Dielectrics
🔌Unit 3 – Electric Circuits
🧲Unit 4 – Magnetic Fields
⚛️Unit 5 – Electromagnetism
📚Study Tools
📚Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.