1.2 Electric Fields & Electric Potential
5 min read•june 18, 2024
Peter Apps
AP Physics C: E&M 💡
26 resourcesSee Units
Electric Fields
Every charged object has an electric field surrounding it, similar to how every object with mass has its own gravitational field. The more charge (or mass) there is, the stronger the field is. The only difference is that while a gravitational field must be attractive, an electric field can be either attractive or repulsive. By convention, we use the direction that a positive test charge will move to draw our electric fields.
Rules for drawing:
- Field lines are vectors and must be drawn with arrows.
- Lines go away from a positive charge and towards a negative charge.
- The strength of the field can be visually represented by the density of the field lines. Therefore field, lines must never touch or cross. This would represent an infinitely strong field.
Later in this guide, we'll cover how to combine these vectors!
Simple Fields
- Point Charges
- Notice the radial symmetry in the fields.
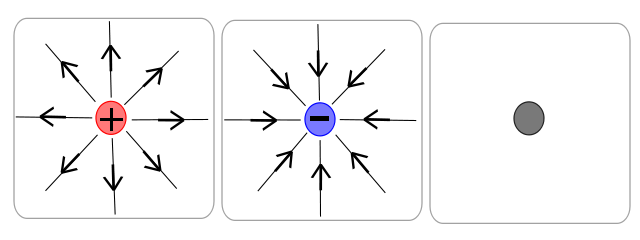
Image from wikimedia.org
- Two Point Charges
Image from Ck12.org
- Two Parallel Plates
- Notice how the field is the same everywhere between the plates.
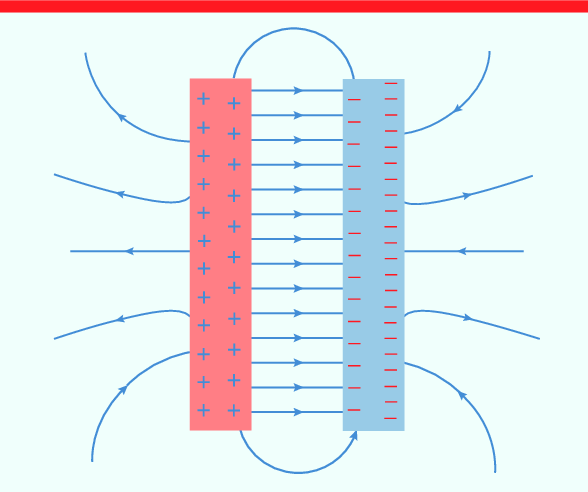
Image from researchgate.net
Try using the PhET simulation to create your own fields and notice the how the field strength changes as a function of charge and distance.
When a point charge is placed in an electric field, we can predict it's change in movement based on the electrostatic force applied. If a positive point charge begins at rest in a rightward pointing electric field, the point charge will accelerate towards the right. If that point charge is instead negative, the point charge will begin to move against the direction of the electric field (to the left).
Electric Field Strength
We've seen visually what electric fields look like. Now it's time to mathematically describe them.
The basic idea is to place a test charge at various locations in the field, measure the electrostatic force at that location, then calculate the field strength. The equation off of your reference tables for electric field strength is:
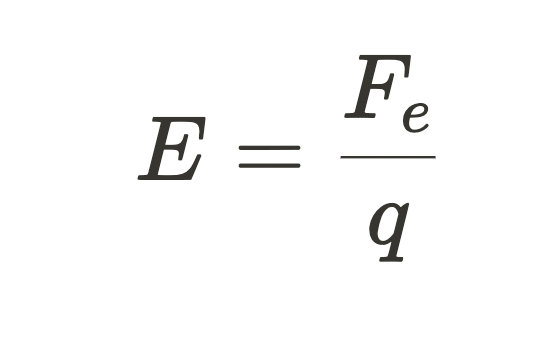
where Fe is the electrostatic force found by using Coulomb's Law, and q is the charge on the test charge used to measure the field.
We can also rearrange the equation to determine E in terms of the charge on the point charge Q.
Remember that net electric fields can also be found by superposition (aka addition) of vectors that represent individual electric fields! To combine vectors of electric fields, you can use two different methods that you use to combine any vectors: the "head-to-tail" method and the "parallelogram" method.
The "head-to-tail" method is when you put the tail (the bottom point) of the first vector against the head (the top point) of the second vector, and then draw a line from the tail of the first vector to the head of the second vector. This line is the combined vector.
The "parallelogram" method is when you put the two vectors so that they have the same starting point, and then draw a diagonal line through the parallelogram (a geometry review: a shape that looks like a rectangle turned on its side) that is formed by the two vectors. The diagonal line is the combined vector.
Both of these methods can be used to add two or more electric field vectors together. The important thing is to make sure that you are using the correct units (usually in V/m) and taking into account the direction of the vectors.
Electric Fields in Conductors & Insulators
Suppose you bring a conductor near a charged object. The side of the conductor closest to the charged object will be induced with the opposite charge. However, the charge will only exist on the surface of the conductor. There will NEVER be an electric field inside a conductor. On the contrary, an insulator can store the charge inside and may have an internal electric field.
Here's an animation from Wikipedia showing how this works in a conductor. When an external electrical field (arrows) is applied, the electrons (little balls) in the metal move to the left side of the cage, giving it a negative charge. The remaining unbalanced charge of the nuclei gives the right side a positive charge. These induced charges create an opposing electric field that cancels the external electric field throughout the box. This is the basic idea behind a Faraday Cage.
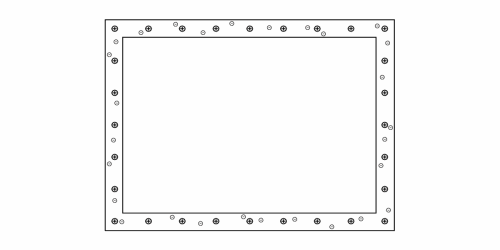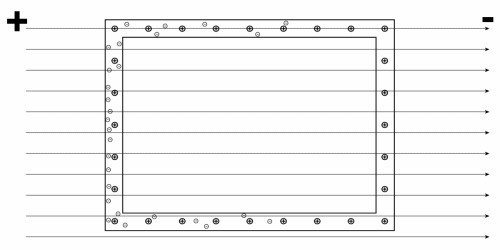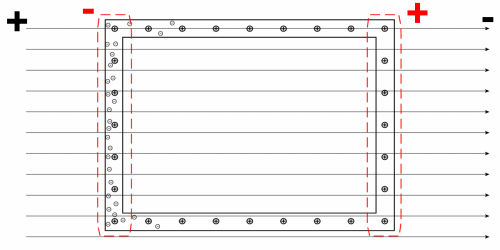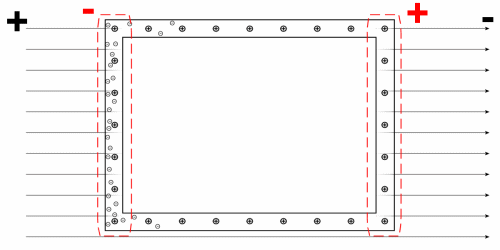
Image from Wikipedia.org
Another way to think about movement of charge is through polarization. When an electric field is present, it can cause a separation of charge within a material. This separation of charge is called polarization.
Imagine you have a balloon filled with air. If you rub the balloon on your hair, it will become charged with static electricity. This is because the rubbing motion causes the electrons in the balloon to become separated from the protons in the balloon, creating a charge on the balloon.
Now, if you bring the charged balloon near a neutral object (with a net charge of 0), like a piece of paper, the electrons in the paper will be attracted to the positive charge on the balloon, and the protons in the paper will be attracted to the negative charge on the balloon. This causes a separation of charge within the paper, with the protons moving towards the negative charge and the electrons moving towards the positive charge.
This separation of charge within the paper is called polarization. The electric field created by the charged balloon is causing the charges within the paper to become separated, or polarized.
1. Ranking the strength (magnitude) of the electric force:
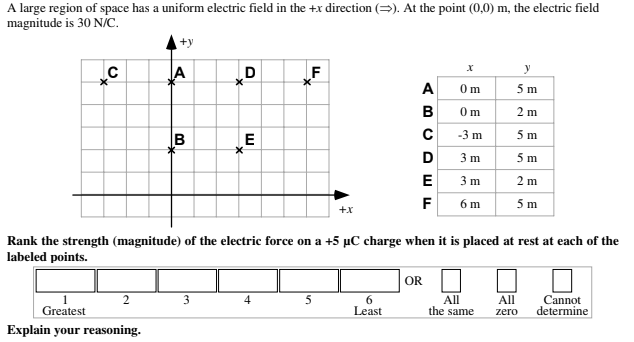
Answer:
The force at each location is the same. The field is uniform so E is constant everywhere and q is the same for each case. Fe = Eq, so the force must be the same.
2. Looking at the graph and details below, determine at which point, if any, the electric field strength is zero.
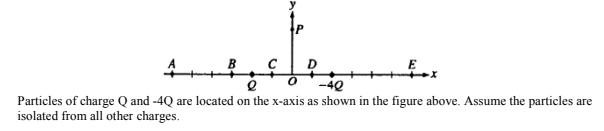
Image from apclassroom.collegeboard.org
Answer:
Point A must have an electric field strength of 0. The point must be closer to the smaller charge (Q) than the larger charge (-4Q), so it can't be D or E. It must also be where the force vectors between the test charge point in the opposite direction so that the net force is 0. Therefore, it can't be point C either. Since the negative charge (-4Q) is 4x greater than the positive charge, the point must be 2x as far from the -4Q charge as it is from the Q charge.
That only leaves A as the answer.
3.

Image from apclassroom.collegeboard.org
Graph A is correct. At x = 2 and x = 4, the distance from the charges is 0, so the field strength must trend towards infinity. At x = 3, the repulsion from the 2 charges cancels out so the field must be 0 there.
Browse Study Guides By Unit
⚡️Unit 1 – Electrostatics
🔋Unit 2 – Conductors, Capacitors, Dielectrics
🔌Unit 3 – Electric Circuits
🧲Unit 4 – Magnetic Fields
⚛️Unit 5 – Electromagnetism
📚Study Tools
📚Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.