1.3 Point Charges - Fields & Potentials
4 min read•june 18, 2024
Peter Apps
AP Physics C: E&M 💡
26 resourcesSee Units
Electric Fields & Work
In order to bring two like charges near each other or to separate two opposite charges, work must be done. Recall from your mechanics courses that W = F*d|| or W = ∫ F*dr, where W is the work done on or by the system, F is the net force, and d is the displacement over which the force is applied. Using this in the context of Coulomb's Law, we get:
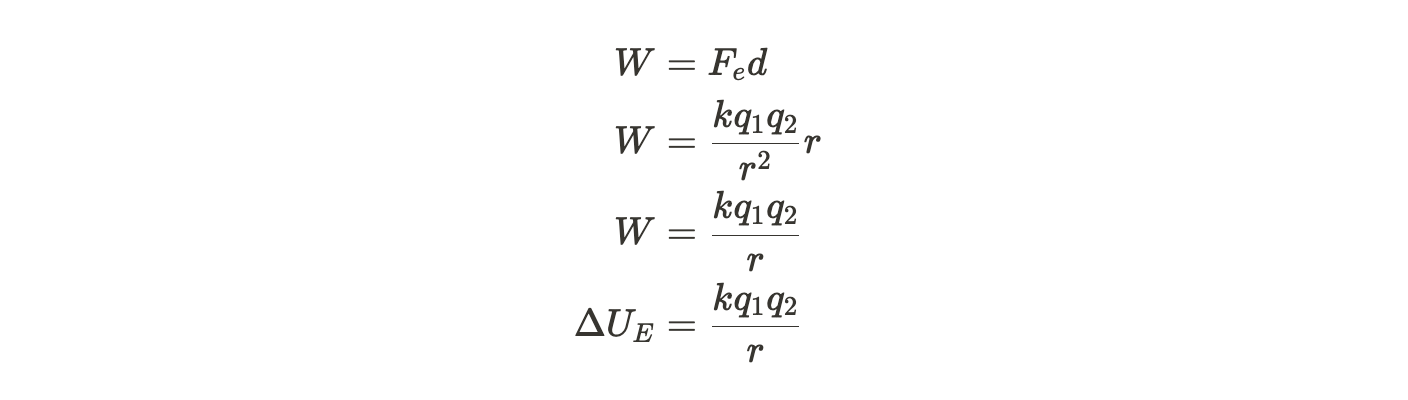
where ∆Ue is the change in Electric Potential Energy. Like all energies, it is a scalar quantity (aka without direction, so not a vector). If you have a collection of charges, the total Ue is the sum of all of the individual Ue with negatives and positives taken into account.
Electric Potential Energy can also be expressed in terms of the Electric Field Strength
E*d is also ∆V so we can find a change in electric potential energy (work) by multiplying a ∆V and q term.
Review Note: Conservation of Energy applies here too!
Potential Difference
Let's take a closer look at that last energy equation we derived. Rearranging it a bit, we get:
The left-hand side of this equation shows the work (or amount of energy) per unit of charge. This "work per charge" quantity is called electric potential or voltage (V).
As we can see here, as r approaches infinity then V approaches 0. This means that at an infinite distance away from a point charge, there is no electric potential from that charge. That info will come in handy later!
Also, if you are dealing with multiple point charges then the total potential can be found by summing all of the individual potentials (V's).
An electrostatic field is a conservative field, and the work done in an electric field in moving a known charge through a known electric field is equivalent to the potential energy (∆Ue) lost or gained by that charge. Changes in kinetic energy can be determined by using the principle of conservation of energy.
Caution:
W or Ue is electric potential energy, measured in Joules. It is NOT the same as potential difference, V, measured in Joules/Coulomb.
Like energy, voltage is a SCALAR. The change may be positive or negative, but that doesn't imply directionality!
Electric Potential of a Point Charge
Let's say you had a positive charge and wanted to map the potential difference around it. The electric field lines move AWAY from the charge. Since V = kQ/r, we can find equal voltages at equal radii from the charge. The equipotential lines would, therefore, look like concentric circles around the charge. Notice how each field line (the blue arrows) intersects at 90° with the equipotential lines.

Since the electric field strength decreases as the radius increases, the voltage must also be decreasing as we travel further away from the charge.
We can determine the change in voltage by doing some calculus. Let's imagine traveling away from the charge from radius a to radius b.
Try using the PhET simulation to create your own fields and notice the how the voltage and equipotential lines change as a function of charge and distance.
Other connections: The idea of equipotential lines with voltage is very similar to topographical maps or barometric pressure maps you may have created in an Earth Science class. In each case, the lines drawn represent areas with the same value: height for topographical maps and pressure for barometric pressure maps
Image from Wikipedia
Image from openstax.org
1.
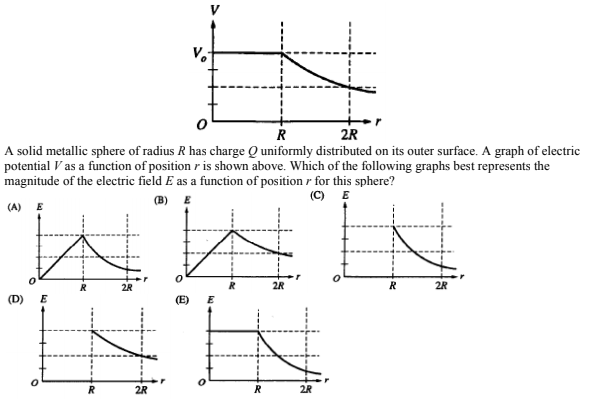
Image from Collegeboard.org
2.

Image from Collegeboard.org
(a) Describe the direction of the electric field at point A.
(b) At which point is the electric field at the greatest magnitude?
(c) How much net work must be done by an external force to move a -1 microCoulomb point charge from rest at point C to rest at point E?
a) The Electric Field Lines point from high potential to low potential and are perpendicular to the equipotential lines. Therefore at point A, the electric field line points up and to the right
b) E is the greatest where the V lines are closest together (largest gradient). This happens at B.
c)
Browse Study Guides By Unit
⚡️Unit 1 – Electrostatics
🔋Unit 2 – Conductors, Capacitors, Dielectrics
🔌Unit 3 – Electric Circuits
🧲Unit 4 – Magnetic Fields
⚛️Unit 5 – Electromagnetism
📚Study Tools
📚Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.