AP Stats Unit 1 Practice FRQ Prompt Answers & Feedback
19 min read•july 11, 2024
Jerry Kosoff
AP Statistics 📊
265 resourcesSee Units
The FRQ section of the AP Stats exam can be tricky. To help, review these student responses to a unit 1 practice prompt, with corresponding feedback from Fiveable teacher Jerry Kosoff!
Unit 1 FRQ Practice Prompt
James drives his car to his job using an identical route each day. He noticed that the time it takes him to get to work (“commute time”) is sometimes impacted by the time at which he leaves his house. For 50 consecutive trips to his job, James noted how long his commute time took (in minutes), as well as whether he left his house before or after 8:00AM. The histograms below show the distribution of commute times on the 24 days he left his house after 8:00AM as well as on the 26 days he left his house before 8:00AM.
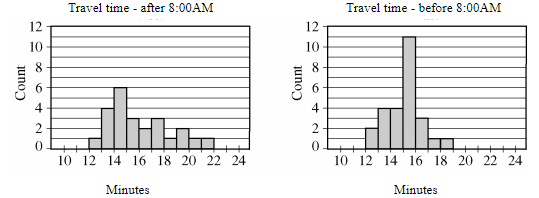
a. Write a few sentences comparing the distribution of commute times for days when James leaves his house before 8:00AM vs the days when James leaves his house after 8:00AM.
b. Based on the histograms, which set of days has a larger mean commute time? Justify your response.
FRQ Practice Submission 1
(a) Both the distributions for James’ commute times for days leaving his house before and after 8:00 am are unimodal with a peak approximately at 14-15 minutes for the travel time after 8 am with it being skewed to the right and a peak at approximately 15-16 minutes before 8 am. There appears to be no unusual features for both travel time distributions. The range of travel time after 8 am appears to be greater than the travel time before 8 am. The median for travel time after 8 am appears to be less than travel time before 8 am.
(b) The set of days after 8 am seems to have a larger mean commute. This is due to the travel time distrubution after 8 am having a right skew which would pull the mean towards the right indicating a larger value. While the set of days before 8 am doesn’t have a right skew so the mean would be smaller compared to travel time after 8 am.
Teacher FRQ Feedback
In part (a), you make a clear comparison of shape, spread, and center, and your answer is in context. Your descriptions of shape are correct, your comparison for spread is correct, but your comparison for center is incorrect (the median time for both distributions is between 15-16 minutes - check it again!). If this were a stand-alone scoring rubric, you would earn a “partial” for this question (having done 3 of the 4 required things). If it had multiple components, you would earn “essentially correct” (E) for all parts except the part that contained the comparison of center.
In part (b), you correct link the shape of the distribution after 8:00am to the likely impact on the mean commute time, AND explain how that is not true in the distribution before 8:00am. You would earn “E” for this portion. Nicely done!
FRQ Practice Submission 2
a) James’ commute time to his work on days where he left the house after 8AM is approximately skewed to the right with a median between 14 and 15 minutes. On the other hand, when James leaves his house before 8AM, the graph of his commute time is approximately normal with a median between 15 and 16 minutes. The range is larger when he leaves after 8AM as compared to when he leaves earlier, and there don’t seem to be any outliers/gaps in either of the histograms.
b) Based on the histograms, the James’ mean commute time when he leaves the house after 8AM is approximately more than when he leaves the house before 8AM. Since the histogram is skewed to the right, that also pulls the mean higher, resulting in a likely higher mean than that of the second graph.
Teacher FRQ Feedback
In part (a), you make a clear comparison between the spread of the two distributions (“the range is larger when he leaves after 8AM as compared to when he leaves earlier”), but you do not do the same for your description of the median time (“on the other hand” does not count as a quantitative comparison). Additionally, check the graphs again - the median for the “after 8:00am” distribution should also be between 15-16 minutes. Your descriptions of shape are correct and your answer is in context. Having done 3 of the 4 components correct (compare shape, compare spread, in context), you would earn “partial” for this question.
In part (b), you make a correct claim about the mean commute time being larger when he leaves after 8AM vs before 8AM, but your explanation could use a little more clarity. When you say “the histogram,” and then “the second graph”, you should be careful to specific which histogram you are referring to, and explain why the “second graph” doesn’t have the same feature as the first. Your answer might get an “E” if the rubric is generous, but would likely earn “P”.
Nicely done - there are a few minor tweaks that will get you up to full credit in no time, so keep practicing!
FRQ Practice Submission 3
A. When James leaves his house after eight am he gets to work in a median time that is between 15 and 16 minutes which is the same median time for if he left before 8 am. Neither graph appears to have any outliers or unusual features. The shape of the graph for leaving after 8 am is skewed right with a peak that is approximately between 14 and 15 minutes while the graph, for before 8 am the graph is unimodal and approximately normal with a peak approximately between 15 and 16 minutes. The range of travel time for after 8 am is at some time between 9 and 10 minutes, which is greater than the range of travel time for before 8 am which is at some time between 6 and 7 minutes.
B. The graph for after 8 am has a greater mean commute time. Since in part A we concluded that both graphs have the same median commute time and the graph for traveltime after 8 am is skewed right we can conclude that the graph for after 8 am has a greater commute time. Since that graph is skewed right we know that the mean is greater than the median. Since there in part A we concluded that travel time is before 8 am is approximately normal we can assume the mean is about the same as the median, which means the mean of the after graph is greater than the before graph.
Teacher FRQ Feedback
In part (a), you make a clear comparison of center (“same median time”), clear comparison of spread (“is greater than the range of travel time for before 8 am”), a correct description of shapes, and your answer is in context. This checks all the scoring boxes, and would earn “E” for essentially correct.
In part (b), you give a clear explanation of why the right-skew in the “after 8 am” distribution would impact the mean commute time, and tie in your work from part (a) to strengthen your argument. This would also earn “E”. You did a good job of giving a thorough answer without “talking too much” and giving up credit that you had already earned. Well done!
FRQ Practice Submission 4
(a) The distribution of travel times after 8am appears to be skewed right while the distribution of travel times after 8am appears approximately normal. The median travel time after 8am is the same for the median travel times before 8am. The range of the travel times before 8am appears to be smaller than the range of travel times after 8am.
(b) The set of data that has a larger mean commute time is the histogram leveled travel time after 8am. This is because the histogram distribution is skewed right meaning the mean is being pulled to the right. In this case, the mean is larger than the median where as the histogram who’s travel time is before 8am would have a similar mean and median since it is approximately normal.
Teacher FRQ Feedback
You’ve done a good job of getting to the point in both parts (a) and (b) and saying exactly what you need to say without much more. Your answer in part (a) includes appropriate comparisons and the context of the problem, and your answer in part (b) mentions the impact of shape on the mean/median in BOTH histograms, which is important for communicating your answer. These should both earn full credit as responses!
FRQ Practice Submission 5
a) After 8am, James’ commute times are unimodal and skewed to the right. His commute time ranges from 12 minutes to 22 minutes. On most days, the commute is about 14-15 minutes. Before 8am, Jame’ commute times are unimodal and relatively symmetrical. The times range from 12 minutes to 19 minutes. The peak commute time is between 15 and 16 minutes.
b) Based on the data, the commute times after 8am likely have a higher mean than before 8am. The graph is skewed right, causing the mean to increase. We can assume that the mean increases beyond that of times before 8am because its graph is not skewed.
Teacher FRQ Feedback
In part (a), you do a good job of describing the distributions of commute times, but you do not compare them. If the AP exam asks you to “compare” distributions, they’re looking for you to use explicit comparison terms, such as “greater than,” “less than,” or “equal to.” Also, be sure to explicitly compare the shape, center, and spread of distributions. You mention the shape and spread of each distribution (without comparing the spreads), but do not give a measure of center for either distribution (mean or median; “peak” is a nice thing to describe but will not count as a measure of center). You could have strengthened your response by adding comparison statements at the end of your paragraph (for example, “the commute times after 8am have a larger range than before 8am”). As it stands now, you would not receive credit for your response.
In part (b), you do a good job of clearly communicating your choice (after 8am) and why it’s your choice (“skewed right”), as well as why the other graph is not your choice (“its graph is not skewed”). Good explanation! This would earn “E” (full credit).
FRQ Practice Submission 6
(a) the median of both the after 8:00am graph and the before 8:00am graph is between 15-16 minutes. the after 8:00 graph has greater variability, range, and higher standard deviation compared to before 8:00; after 8:00 graph is also skewed slightly right. before 8:00 is normal with a jutting peak from 15-16 mins. since before 8:00 graph is normally distributed, its mean will also be between 15-16. on the other hand the after 8:00 graph is skewed right, the mean will be pulled up, resulting in a higher mean than median. both graphs are unimodal.
(b) as discussed in (a), the set of days after 8:00 has a higher mean. while both medians are between 15-16 mins, this set is skewed right, thus dragging the mean upwards.
Teacher FRQ Feedback
In part (a), you do a good job of comparing the distributions in context. Your comparison of medians is correct, and your comparison of spread is correct (quick note - you could have used “variability”, “range”, or “standard deviation” to make these comparisons - you did not need to include all three statements Similarly, you only need to compare one of the two measures of center - median or mean). Be careful with your descriptions of shape - you called the before 8:00am graph “normal”. While it would be fair to call it “approximately normal,” to be a true “normal” distribution the graph would have to meet certain criteria that we are not able to check without more information. On some rubrics, that would ding you and prevent you from earning full credit. Really, any time you want to say something is “normal” on the AP exam, you should add “approximately” to it (unless you’re explicitly told something is in fact Normal).
In part (b), you do a good job of clearly explaining your choice of graph, and connecting it to the fact that skew impacts the mean. You would likely earn full credit.
FRQ Practice Submission 7
a.) The histogram comparing the commute times for days when James leaves his house before 8:00 AM is unimodal vs the days when James leaves his house after 8:00 AM is slightly skewed right. There is a peak at 14-15 minutes after 8:00 AM and a peak at 15-16 minutes before 8:00 AM. The median for both distributions is between 15-16 minutes. There are no apparent gaps/outliers in the histograms. The range of travel times for after 8:00 AM is bigger at between 12 to 22 minutes, while the range of travel times for before 8:00 AM is between 12 to 19 minutes.
b.) Based on the histogram, the set of days after 8:00 AM travel time has a larger mean commute because of the slight skew to the right. The right skewness will increase the mean, while the travel time before 8:00 AM does not have a skew to right causing it to have a smaller mean.
Teacher FRQ Feedback
In part (a), you do a good job of making in-context comparisons, correctly comparing the median and range for the two distributions, and making comments on the lack of obvious outliers. Be careful with your shape comments - typically the description “unimodal” by itself is not enough to earn full credit (as a distribution can be unimodal and symmetric, or unimodal and skewed). “Bimodal” by itself is a good description for shape, but you should include “approximately symmetric” or “skewed to the ___” with any unimodal description.
In part (b), you choose the correct histogram and clearly defend your choice with a reference to the mean being impacted by the skew of the histogram. Nice job!
FRQ Practice Submission 8
a. The distribution of James’s commute time took for after 8:00 am is unimodal and skewed to the right while the distribution of James’s commute time took for before 8:00 am is unimodal and fairly symmetric. The center for the histogram for travel time after 8:00 am is the same as travel time before 8:00 am. The distribution of commute time for after 8:00 am has a larger spread than before 8:00 am. There is no apparent outlier.
b. The distribution of commute time for after 8:00 am has a larger mean. Looking at the graphs, the distribution for commute time for after 8:00 am is skewed right meaning the mean is being pulled to the larger values while the distribution of commute time before 8 am is fairly symmetric. A distribution that is highly right-skewed is likely to have a substantially larger difference between the mean and median.
Given that the median of both distributions is roughly the same, so it makes sense that the highly right-skewed distribution (after 8:00 am) is the one with the bigger gap between the mean and median compared to a more symmetric and, therefore, the one with the higher mean commute time.
Teacher FRQ Feedback
In part (a), you make clear comparisons of center, shape, and spread in context of the scenario. One thing to be careful with is your mention of “the center” being the same. As you (correctly) argue in part (b), the median travel times are within the same range, but the mean travel times are not, due to the skewness of the “after 8:00am” graph. Therefore, your use of the generic term “center” may be penalized, as there are two measures of center you may be referring to (median/mean) and only one of them is likely “the same.” It’s important to be specific in cases like that.
As mentioned, your answer to part (b) is very good - it thoroughly explains your choice and why the other choice is incorrect. Well done!
FRQ Practice Submission 9
a.) The distribution of commute times before 8:00 am is more symmetric with a mean of approximately 15 min. it is also less variable than the distribution of times after 8:00 am with Range(before)= 7 and Range(after)= 10. The distribution of commute times after 8:00 am is more right skewed with a median around 15. (using median instead of the mean to determine the center because of its resistance to skews).
b.) Due to the apparent right skew in the after 8:00 am distribution, the mean (being non-resistant to skew) will be larger than the mean from the before 8:00 am distribution that has a symmetric shape, leaving the mean at approximately 15 minutes.
Teacher FRQ Feedback
In part (a), you make a clear comparison of the shapes of the graphs and a clear comparison of the spread/variability. [Sidenote: be careful talking about ranges on histograms. The ranges are approximately 7 and approximately 10 minutes, respectively, because the numbers on the x-axis for a histogram are endpoints of intervals. The longest commute time after 8:00am may not have been exactly 22 minutes; it could have been 21.6 minutes.] Unfortunately, even though you name the mean/median (center) for each distribution, you don’t ever explicitly compare them, as the prompt asks. When asked to compare distributions, you must make an explicit comparison (“less than,” “more than,” “equal to”, “similar to”, etc). Even though you imply the centers are similarly around 15 minutes, you have to spell it out for us.
In part (b), you correctly cite the right-skew having an impact on the mean and choose the correct distribution (and explain why the other one is wrong), but I think you have some typos (you say “mean” every time but I think you meant to say “median” at least once there).
FRQ Practice Submission 10
a) The distribution of commute times for days when James leaves his house before 8:00 AM is approximately normal and strongly skewed right. The center (median) of the distribution is approximately between 15 and 16 minutes.The spread (range) of the distribution is 10 minutes. There are no gaps or outliers in the distribution.
Comparatively, the distribution of commute times for days when James leaves his house after 8:00 Am is fairly symmetrical. The center (median) of the distribution is between 15 and 16 minutes. The spread (range) of the distribution is 7 minutes. Additionally, there are no gaps or outliers in the distribution.
b) Since the normal distribution of commute times for days when James leaves his house before 8:00 AM is strongly skewed right, the mean will be greater than the median. Since the normal distribution of commute times for days when James leaves his house after 8:00 Am is fairly symmetrical, the mean will equal the median. Thus, the days when James leaves his house before 8:00 AM will have a larger commute time.
Teacher FRQ Feedback
In reading your descriptions, I think you may have switched labels in part (a) - it looks like the first thing you describe is the “after” graph (range of 10, skewed right, etc)… but you called it the “before” graph. Additionally, while you give good descriptions, you don’t ever compare the centers & spreads explicitly. When asked to do a comparison of graphs, we have to “spell it out” by saying things like “greater than,” “less than,” etc. Also, some things to be careful with in your descriptions: (1) it’s impossible for a distribution to be both “approximately normal” and “strongly skewed right”, (2) when discussing range on a histogram, we must use language like “approximately 10 minutes” - we can’t actually be sure what the max/min values are unless we’re explicitly told. (example: the shortest commute time might be 12.4 minutes). I don’t mean this to sound like your response was all bad - you clearly have some understanding here - but I do want you to know how to attack these kinds of questions.
Moving on to part (b), you give a clear explanation of your choice, with correct reasoning in both cases. Well done!
FRQ Practice Submission 11
A. The distributions of commute times on the 24 days he left after 8 am and the 26 days he left before 8 am both do not contain any outliers, and both their medians are about the same (approximately 15-16 minutes). However, the shape of the distribution of commute times on the 24 days he left his house after 8 am is more skewed (specifically to the right) than the distribution of commute times on the 26 days he left his house before 8 am (which is more unimodal). Also, the spread of the distribution of commute times on the 24 days he left after 8 am is larger than the spread of the distribution of commute times on the 26 days he left before 8 am.
B. The distribution of commute times on the 24 days he left after 8 am has the larger mean commute times in minutes. The medians of both the distributions are about the same — approximately 15-16 minutes. But since the distribution of commute times on the 24 days he left after 8 am is skewed to the right, this means its mean is greater than its median. And since the distribution of commute times on the 26 days he left before 8 am is more unimodal, this means its mean equals its median. So, therefore the mean of the distribution of commute times on the 24 days he left after 8 am is larger than the mean of the distribution of commute times on the 26 days he left before 8 am.
Teacher FRQ Feedback
Your answer to part (a) is very thorough, and addresses the scenario in context with comparisons of center, shape, spread, and a discussion of outliers. One small thing - be careful in your shape comparisons. It’s good to describe the after 8am times as skewed, but “unimodal” by itself for the before 8am times is a little too general. “Bimodal” as a shape can count as full credit, but “unimodal” typically does not - as you can be unimodal and symmetric or unimodal and skewed (in fact, the after 8am graph is unimodal as well in this case). You should go with something like “more symmetric” to earn the full credit.
In part (b), you give a very clear (correct) answer with reasons relating to the shape of the graph. I have the same note about “unimodal” vs “symmetric”.
FRQ Practice Submission 12
a) Comparing the distribution of commute times for days when James leaves his house before 8:00AM vs the days when James leaves his house after 8:00AM we observe that both are unimodal however after 8 is right-skewed while before 8 is roughly symmetrical. Also after 8 has a median between 15-16 while before 8 also has a median between 15-16. After 8 has a larger spread with a range of about 10 minutes while before 8 has a range of only 7 minutes. Lastly, neither distribution has any outliers as all values fall within the inner/outer fences.
b) After 8 will have a smaller mean as the majority of data is to the left where the time would be smaller whereas before 8 is roughly symmetrical meaning that the mean won’t be pulled as far left as in the other distribution. THus before 8 will have a larger commute time.
Teacher FRQ Feedback
In part (a), you give a very thorough comparison, including shapes, center, and spread. You also say “about 10 minutes” for the range after 8am, which is important on histograms (as you can’t know the min/max values for sure).
In part (b), you pick the wrong distribution. Remember that the mean is impacted by skew/outliers - so the majority of data on the left (AKA skewed right) will actually have a higher mean than median (as the few data points on the right will skew the mean, but not the median). Therefore, it is the after 8am distribution in this case.
FRQ Practice Submission 13
a) the distribution when James leaves his house before 8:00am has a roughly symmetric shape whereas the other distribution it’s skewed to the right. the distribution for the travel time before 8 has a range of 7 and the other one has a range of 10.
they have roughly the same median at 15-16 minutes. there seem to be no outliers.
b) since the graph is skewed to the right it means that its mean will be greater than the mean of the distribution of travel time before 8. this is because the graph is skewed and since the mean is non resistant to outlier it will get pulled towards the tail but towards the tail in this situation there are larger values which would make the mean greater.
Teacher FRQ Feedback
In part (a), you provide appropriate descriptions of center, shape, and spread for each of the distributions, but you do not provide comparisons. Comparisons in AP Stats involve explicit comparison words like “more,” “less,” “about the same as,” etc. For an example of this in action, see the post shortly above yours by user “abar2648”.
In part (b), you give a clear description of how mean is impacted by the skew in the after 8am distribution. Nice job.
FRQ Practice Submission 14
a) the distribution of travel time after 8 am is slightly skewed to t he right while the distribution of travel time before 8am is approximately normal. both do not have any potential outliers. the center is the same for both distributions at 15-16 and the spread is larger for the distribution of travel time after 8 than before 8.
b) the distribution of travel time for after 8 am has a larger mean as the median for both distributions is 15-16 but since the distribution for before 8 is approximately normal, the mean will be a similar value to the median but the distribution of after 8 is skewed to the right which means the mean will be pulled to the tail, in this case towards a higher value. Therefore the distribution of travel time for after 8am will have a higher mean.
Teacher FRQ Feedback
Nice responses! You have clear comparisons in part (a) of center, shape, and spread. You could strengthen part (a) by referring to “median” as your measure of center in this part - the means will likely be different as you correctly defend in part (b).
a. On the graph of days when James leaves his house after 8 am the shape is fairly unimodal with a right skew whereas in the graph for before 8 am the shape is unimodal and moderately symmetric. The center for both graphs, according to the median appears to be between 15 and 16 minutes for his commute time. The spread for travel time after 8 am is greater than the spread for travel time before 8 am. Neither graph seems to show any apparent outliers.
b. The graph showing travel time after 8 am has a larger mean commute time because, while the median shows both graphs having a similar center, the mean is pulled in the direction of skew so since the after 8 am graph is skewed to the right, it pulls the mean up making it larger than the travel time before 8 am because that one is fairly symmetric.
Teacher FRQ Feedback
Both answers are very solid and written in a way that would earn points on typical rubrics. You provide clear comparisons in part (a) of center, shape, and spread, and provide a strong description in part (b) that is in context and mentions both distributions. Nice job!
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.