AP Stats Unit 7 FRQ Practice Prompt (#1) Answers & Feedback
12 min read•july 11, 2024
Jerry Kosoff
AP Statistics 📊
265 resourcesSee Units
FRQ practice is one of the most important ways to prepare for the AP Stats exam! Review these student responses to a unit 7 prompt and their corresponding feedback from Fiveable teacher Jerry Kosoff!
FRQ Unit 7 Exam Practice Prompt
A manufacturer of potato chips advertises that each bag contains 10 ounces of chips. However, the production lines at the manufacturer (which produce thousands of bags of chips per day) do not always fill each bag with exactly 10 ounces. Throughout the day, quality control staff at the manufacturer select random samples of bags on a selected production line and conduct a hypothesis test with the following null and alternative hypotheses:
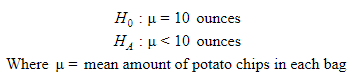
If enough evidence is found to reject the null hypothesis in favor of the alternative, the production line is shut down and re-calibrated.
a. Describe a Type II error in the context of the manufacturer’s hypothesis test, and identify a possible consequence of making a Type II error.
b. In a random sample of 35 bags of chips, the mean weight is 9.9 ounces with a standard deviation of 0.45 ounces. At the significance level of 0.05, should the company shut down the production line? Justify your response.
FRQ Writing Samples and Feedback
FRQ Practice Submission 1
a) A Type II error means that we fail to reject H_0 and the potato chips manufacturer advertised bag chip amount of 10 ounces reflects the mean amount of potato chips in each bag, when we should’ve have rejected H_0, as there should have been convincing evidence to find that the mean amount of potato chips in each bag is less than 10 ounces. The consequence of making a Type II error is that the production line was not shut down and not re-calibrated when it should’ve been shut down and re-calibrated.
b) mu = the mean amount of potato chips in bags like the ones at the production lines
H_0: mu = 10 ounces, H_A: mu < 10 ounces
One-sample t test for mu
Conditions:
- Random - Stated that quality control staff selected random samples of bags
- 10% Condition for Independence - Safe to assume there are at least 35(10) = 350 bags of chips at the production line
- Normal/Large Sample Condition - Since n = 35 >= 30, the Normal/Large Sample Condition is satisfied, thus the sampling distribution of x-bar is approximately normal.
x-bar = 9.9, S = 0.45, n = 35, df = 34, t* = -1.31468 from invt on TI calculator with df = 34 and area = 0.025
P-value = P(t* < -1.314) = 0.098 from tcdf on TI Calculator
Since 0.098 > alpha of 0.05, we fail to reject H_0.
At a level of significance of 0.05, we fail to reject the null hypothesis since there is not convincing evidence that the true mean amount of potato chips in each bag is less than 10 ounces.
Teacher FRQ Feedback
No facepalms here! Strong execution in part (a) with your description of a Type II error. In part (b), you execute the test well from start to finish, reaching the appropriate conclusion (which hopefully for the chip manufacturer isn’t a Type II error since we failed to reject Ho!). One little thing: you didn’t address the question of if the line would get shut down (it wouldn’t). Be sure to read the actual question carefully - we might have to connect our conclusion in the hypothesis test to the scenario at hand.
FRQ Practice Submission 2
a) A type 2 error means that the manufacturer will fail to reject a false H0. This means that they will say that the mean amount of potato chips in each bag is equal to 10, when in fact it is less than 10 oz. This means that the company should have shut down and re-calibrated their machines, but they didn’t. Some customers are going to get bags of chips that are less than what the company says is true.
b)conditions:
- SRS- “random sample of 35 bags of chips” --> stated in the proble
- independence- 10(35)=350 < population of bags of potato chips
- normal- 35>30 --> Central Limit Theorem is applied (normal distribution)
solve: z=9.9-10/(.45/sqrt.(35)) = 1.31 --> .0951
p-value: .0951
(.0951>.05 significance level) --> Fail to Reject the H0. There is marginal evidence that supports the mean amount of potato chips in each bag is less than 10 ounces, therefore, the line would not shut down and recalibrate the machines.
Teacher FRQ Feedback
In part (a), you correctly describe a type II error and a possible consequence. Be careful with your wording - failing to reject Ho does not necessarily mean we will conclude the mean amount is equal to 10, just that we will not have evidence to conclude that it’s less than 10 oz. (“fail to reject Ho” is not the same as “accept Ho”, and your response makes it sound like we “accept Ho”.)
In part (b), you check the appropriate conditions, but then run a z-test. Z-tests are for proportions (unless we know the population standard deviation, which we don’t) - this should be a “t-test” with a t test statistic. Your p-value and conclusion you get from your z-test are consistent, though, so while you would get partial credit for choosing the test, you would get full credit for your conditions and your conclusion.
FRQ Practice Submission 3
a) a type 2 error would mean that the manufacturer railed to reject the null when in reality he should have rejected the null. this means that he concluded that the machine is filling the bag till 10 ounces when in reality. its putting less than 10 ounces into each chip bag. This may lead to customer dissatisfaction, false advertisement and also the manufacturer will not recalibrate or fix the machine
Teacher FRQ Feedback
On part (a), you appropriately define a type II error in this context. Your sentence about the possible consequence only really needs to list one reason (“identify A possible consequence”), so be sure to fully explain just your one. For example, in this case you could say “This may lead to customer dissatisfaction because they will be getting less than the advertised amount” or “this means that the manufacturer will not fix the machine that is broken and needs to be fixed.”
FRQ Practice Submission 4
a. The is not sufficient evidence to suggest that the mean amount of potato chips in each bag is less than 10 ounces, when in reality the mean amount of potato chips in each bag is less than 10 ounces. A consequence of making a type II error is that the customers get less chips per bag and still have to pay full price for a bag that weighs less than 10 ounces.
b. No
Assumptions:
- We have a random sample of bags of chips.
- Population of chips is at least 350
- Since n is large enough due to CLT, the sampling distribution is approximately normal.
- Standard deviation is known
Hypothesis
H_o: mu = 10
H_a: mu < 10
Where mu is the true mean amount of potato chips in each bag
Calculations
t = (xbar - mu)/(standard deviation/sqrt(n)
t = (9.9-10)/(0.45/sqrt(35))
t = -1.3146
p-value = tcdf(-1E99, -1.3146, 34)
p-value = 0.0987
alpha = 0.05
p-value > alpha
Conclusion
Since the p-value > alpha, we fail to reject the Ho. There is not sufficient evidence to suggest that the true mean amount of potato chips in each bag is less than 10 ounces.
Teacher FRQ Feedback
Nicely done! You give a clear and in-context description of the Error in part (a), and do all appropriate steps in part (b).
FRQ Practice Submission 5
a) A Type 2 error would be that the mean amount of potato chips is less then 10 ounces, but the system doesn’t detect it and the production line keeps going. A consequence of this would be getting a lot of complaints and possibly losing money and getting a bad image because the potato chip bags are all providing less chips than they claim to.
b) Conditions:
- random: question states they took “a random sample”
- normal: sample size is greater than 30, (35>30), so according to the CLT, we can assume normality.
- independence: we can assume there are greater than 35(10) 350 bags of chips in the whole population so the independence condition is met.
one sample t test for population mean
t= -0.1/0.076 = -1.315
tcdf:
lowerbd: -9999
upperbd: -1.315
df: (35-1)= 34
p-value: 0.097
Since our p-value of 0.097 is greater than our significance level (alpha=0.05). we fail to reject our null hypothesis. There is insufficient evidence that the company should shut down the production line.
Teacher FRQ Feedback
Nice work on both parts - in part (a) you appropriate define a Type II error in this context and give a reasonable consequence. In part (b) you name the appropriate test, check conditions, and execute correctly including the correct decision based on the p-value, stated in context.
FRQ Practice Submission 6
a)A type 2 error is when you fail to reject the Ho or reject Ha incorrectly.
This means that they will conclude the bags contain 10 ounces when they contain less than that. The consequence here would be that the production line would continue when it should be re-calibrated.
b)
Identify)
µ=mean amount of potato chips in each bag

t test for mean
Conditions:
- Random: We were told the sample was randomly selected.
- Normal: The sampling distribution is approximately normal because n>=30 (35>30)
- 10% Condition: There are more than 10×35 bags of chips on the production line.
Calculations:
- tTest(µ0=10, x¯=9.9, Sx=0.45, n=35)=-1.31468
- p-value=0.098708
Interpretation:
Because the p-value(0.098708) is not below the alpha(0.05), we fail to reject the null hypothesis(Ho). There is not significant evidence that the company shut down the production line.
Teacher FRQ Feedback
Excellent work on the hypothesis test in part (b) [shout out to the copy-paste of the parameters and hypotheses!]. Be careful in your description of part (a). You mention that a Type II error is when we fail to reject Ho… but that is not the same as accepting Ha. We should never use the word “accept” when talking about Ho or Ha. We either reject/fail to reject Ho, and find evidence for/don’t find evidence for Ha. So a Type II error is when we fail to reject Ho when Ha is really true, so we should find evidence for it. Furthermore, you don’t mention the mean in your description (it’s not that each individual bag of chips would have less than 10 oz, it’s that the mean would be less than 10 oz). With the incomplete description of the Type II error (but correct description of the consequence), you would likely earn partial credit for part (a).
FRQ Practice Submission 7
A) type 2 error would be when the manufactures accidentally retains the null, which is that the bags contain 10 ounces of chips in reality when the production line does not fill up to 10 ounces, it fills less.
B) Plan step is already done for you.
Model:
A/C:
- Random: It is given that the manufactures selects it at random
- 10%: 35 bags <= 10% of all the bags produced at the line (most likely). Since we have satisfied these conditions, we can assume independence for the chips bags
- Normality: Since n>30 (35>30), this condition is satisfied. Since normality is satisfied, we can assume the sample is large enough.
Mechanics:
xbar= 9.9
SE(Estimate)= s/sqrt(n)=0.076
z= (9.9-10)/s/sqrt(n)= -1.31
df= n-1 = 34
pvalue: tcdf(lower: -99999, upper: -1.31, df=34)= 0.099
Conclude:
In this instance, 0.099>0.05 (not statistically significant), meaning we should retain the null hypothesis because the evidence is not convincing, in context basically saying the company should not shut down the current production line.
Teacher FRQ Feedback
Solid work! Be careful when you say “retain the null.” That almost makes it sound like you’re accepting the null hypothesis, which we don’t do. Safer to say “fail to reject the null” or “do not reject the null.” Your work in part (b) has all appropriate components. In part (a), you would probably only get partial credit, because you never mention that we’re dealing with the mean amount in the chip bags, not the amounts in individual chip bags. So we should say “the bags contain a mean of 10 ounces of chips when in reality the production line has a mean of less than 10 ounces”, or something similar.
FRQ Practice Submission 8
a) A Type II error in context would be that you fail to reject the null hypothesis or you agree that each bag has 10 chips when in reality, there is statistically significant evidence to reject the null hypothesis, or there are not 10 chips in every bag. The consequence of this would be that the manufacturer is putting less chips in each bag which means the customer is paying for a less than sufficient amount of chips.
b.) μ = mean amount of potato chips in each bag
Ho: μ=10 ounces
Ha: μ<10 ounces
Conditions:
- Random: We are told they are using a “random sample of 35 bags of chips”
- Normal: It is normal because 35>30
- 10% condition: There are more than 35 x 10 bags of chips in the production lines
Calculate: t= 9.9-10/ .45/sqrt35 = -1.315
p-value: .0987
Interpret: Because our p-value (.0987) is not below the alpha(0.05) we fail to reject the Ho. There is not significant evidence that the production line should be shut down and re-calibrated.
Teacher FRQ Feedback
In part (a), you demonstrate an understanding of Type II errors but do not quite explain this context properly. The hypothesis test isn’t about whether each bag has 10 chips (as you imply), it’s about whether the mean weight in the bags is 10 ounces. So individual bags may very well have 10 ounces, as they are supposed to, but the overall average may be lower than that due to bags with less. In part b, you appropriately conduct the test and reach the correct conclusion.
FRQ Practice Submission 9
a) A Type II error is where we fail to reject H0 when we should have, which means that the test provided statistical evidence that the the average weight of the potato chip bags was 10 ounces when it shouldn’t have. A consequence of this is that the line is not shut down and not re-calibrated when it should have been shut down and re-calibrated.
b) μ is the mean weight of the potato chip bags by the manufacturer.
H0:μ=10
Ha:μ<10
Conditions:
- Random: “In a random sample of 35 bags of chips”
- Normal: Because 35 ≥ 30, the data is approximately normal
- Independent: It is reasonable to assume that the population of the potato chip bags produced by the manufacturer is at least 350.
We will conduct a one-sample t-test for population means
Calculations:
p=0.098,df=34
Conclusion:
Because 0.098>α , which is 0.05, we fail to reject the H0 . We have convincing statistical evidence that the mean weight of the potato chip bags made by the manufacturer is not less than 10 ounces.
Teacher FRQ Feedback
Nice work on both parts - you describe a Type II error using appropriate context, and conduct an appropriate hypothesis test in part b, reaching the correct conclusion.
FRQ Practice Submission 10
a. A type II error in this case would be failing to reject Ho when it’s false. This means that the control staff would conclude that the true mean amount of potato chips in each bag really does equal 10 ounces when in fact the true mean is less than 10 ounces. This would be bad because the production line would keep running while producing chip bags with a true mean of less than 10 ounces and would be lying to their customers about the chip bag quantity.
b. state: Ho: mu=10 ounces Ha: mu<10 ounces where mu is the true mean weight of all bags of potato chips that the company manufactures
plan: one sample t-test for mu(sigma unknown)
randomness: stated that control staff selected random samples of bags
normality: 35>30 so CLT applies
10% condition: 35(10)=350 bags which is less than 10% of the “thousands of bags of chips per day” being produced
do: t= -1.31
p-value=.098
df=34
conclude: due to our high p value of .098 which is greater than alpha=.05 we fail to reject Ho. There is insufficient evidence to conclude that the company should shut down the production line.
Teacher FRQ Feedback
Good work! In part (a) you appropriately define a Type II error in this context; in part (b) you execute the hypothesis test appropriately
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.