📚

All Subjects

📊

AP Stats

✳️

Unit 8

8.2 Setting Up a Chi Square Goodness of Fit Test

6 min read•june 18, 2024

Josh Argo

Jed Quiaoit

AP Statistics 📊

265 resources

See Units

Expected Counts (and the Unexpected?)

In a statistical test, the expected count is the number of observations that you would expect to see in a particular category if the null hypothesis were true. The null hypothesis is a statistical hypothesis that states that there is no difference between the variables being tested. 🔢

To calculate the expected count for a particular category, you would take the sample size and multiply it by the probability of being in that category under the null hypothesis. For example, if you have a sample of 1000 people and the null hypothesis is that there is no difference in political party affiliation between men and women, you would calculate the expected counts for men and women separately by multiplying the sample size by the probability of being a man or woman.

Expected counts are used in statistical tests to determine whether the observed counts are significantly different from what you would expect to see if the null hypothesis were true. If the observed counts are significantly different from the expected counts, then you can conclude that the null hypothesis is not true and that there is a difference between the variables! 👍

Tying Into Chi-Squares

Now that we've added more context on why expected counts play a role in chi-square distributions, let's briefly touch upon the chi-square statistic. 🟩

The chi-square statistic is a measure of the difference between the observed counts and the expected counts in a statistical test. It is calculated by summing the squared differences between the observed and expected counts, divided by the expected counts, for each category.

The chi-square statistic is used to determine whether there is a significant difference between the observed counts and the expected counts, which would indicate that the null hypothesis is not true. The larger the chi-square statistic, the greater the difference between the observed and expected counts and the less likely it is that the difference is due to chance.

To determine whether the chi-square statistic is statistically significant, you would use a chi-square table or a computer program to calculate the p-value, which is a measure of the likelihood that the observed difference between the variables occurred by chance. If the p-value is below a certain threshold (e.g., 0.05), then you can conclude that there is a significant difference between the observed and expected counts and that the null hypothesis is not true.

Chi-Square Distributions

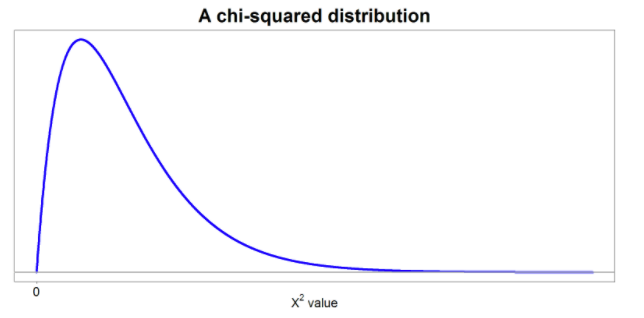
Source: StatKat

The chi-square distribution is a continuous probability distribution that is used to describe the distribution of a chi-square statistic. It has only positive values and is skewed to the right as shown in the image above, meaning that it is more heavily concentrated on the left side of the distribution.

The chi-square distribution is defined by a parameter called the degrees of freedom, which is a measure of the number of independent pieces of information that are used to calculate the chi-square statistic. The degrees of freedom for a chi-square test are equal to the number of categories minus 1. As the degrees of freedom increase, the skew of the chi-square distribution becomes less pronounced and the distribution becomes more symmetric. 📈

Goodness of Fit

The first variation of a chi-squared test we will run is a chi-square goodness of fit test!

A chi-square goodness of fit (GOF) test is a statistical test that is used to determine whether the observed frequencies of a categorical variable differ significantly from a reference distribution. It is used to evaluate the fit of one categorical variable with multiple categories (e.g., a variable with more than two categories). In other words, a GOF test is used when evaluating the fit of one categorical variable with multiple categories. In previous units where we only observed one categorical variable, we were limited to two categories (so only binary examples). 💠

For instance, we could look at a group of people and whether they answered yes or no, but we could not determine if they answered on a scale of 1 to 5. Since a scale of 1 to 5 would have 5 categories that participants could fall into, we could not perform a 1 Prop Z Test, so we would have to use something a bit more complex, like a chi-squared goodness of fit test.

Parameters

It is important to specify what our parameters are when performing inference. In the case of chi-squared GOF tests, we will have multiple population proportions that we are trying to check against a claim.

For example, if we survey a group of people on their scale of happiness 1-5 with 5 being the happiest and we have a claim that says:

10% said they were unhappy (1),
15% said they were somewhat unhappy (2),
28% said they were sometimes happy and sometimes sad (3),
30% said they were happy (4), and
17% said they were always happy (5)

Then our parameter we would be testing would be the true proportion of 1s, 2s, 3s, 4s and 5s.

Hypotheses

Null Hypothesis

Just as with any inference test, we must have both a null hypothesis and an alternate hypothesis. Our null hypothesis is generally what we would expect to happen if everything goes according to plan. There is nothing different going on than what our original claim was.

In the example of our happiness scale of 1-5, our null hypothesis would be as follows: 😊

H0: p1 = 0.1

p2 = 0.15

p3 = 0.28

p4 = 0.3

p5 = 0.17

It is very important when writing our hypotheses to include context. In the example that we have just done, adding a subscript of 1, 2, 3, 4, or 5 gives us context since the problem was dealing with a survey score of 1 to 5. It is also a good idea to identify p1=true proportion of people who rated 1 as their happiness score, etc. for other scores. 💯

Alternate Hypothesis

Our null hypothesis is normally very simple. It is best to just state that at least one of the proportions in our null hypothesis is incorrect. Since all of our proportions add up to 100%, one of our null proportions being incorrect leads to others being incorrect as well.

For example, on the happiness scale problem as noted above, our alternate hypothesis would be:

Ha: At least one of the proportions measuring people’s happiness is incorrect.

As always, context is key and can cause points to be docked off in FRQs!

Conditions

Chi-squared tests require two similar conditions as previous inference tests: 🤔

Our sample must be random
10% rule: Our population must be at least 10x our sample

Instead of checking for a normal distribution, we have to make sure that our expected counts are at least 5.

In our happiness scale example, we would take our sample size and multiply by 0.1, 0.15, 0.28, 0.3 and 0.17 to ensure that we would expect to have at least 5 fall into each category.

If performing an experiment by random assignment of treatments, the independence condition is assumed (10% condition) and the random assignment suffices for the random condition.

Example

A recent survey established that when choosing their favorite between Harry Potter, Lord of the Rings and Star Wars, the answers were the same with 1/3 picking each of the series.

To test this claim, a random sample of 2500 US adults was surveyed about their favorite movie/book series. To check this test, write your hypotheses and check conditions for inference. 📚

Hypotheses and Parameter

H0: pHP = 0.33, pSW = 0.33, pLOTR = 0.33

Ha: At least one of the proportions of favorite movie/book series is incorrect.

pHP=true proportion of people who prefer Harry Potter,

pSW=true proportion of people who prefer Star Wars,

pLOTR=true proportion of people who prefer Lord of the Rings

Conditions

Random: “A random sample of 2500 US adults” (quote the problem)
Independence: It is reasonable to believe that there are 25,000 adults in the US (10% condition)
Large Counts: 2500(0.33)=825>5 (same for all three proportions)

In the next section, we will finish the problem by going through and calculating our test statistic and p-value based on our actual counts from our sample. 🏀

🎥 Watch: AP Stats Unit 8 - Chi Squared Tests

Browse Study Guides By Unit

👆Unit 1 – Exploring One-Variable Data

✌️Unit 2 – Exploring Two-Variable Data

🔎Unit 3 – Collecting Data

🎲Unit 4 – Probability, Random Variables, & Probability Distributions

📊Unit 5 – Sampling Distributions

⚖️Unit 6 – Proportions

😼Unit 7 – Means

✳️Unit 8 – Chi-Squares

8.0Unit 8 Overview: Chi Square

8.1Introducing Statistics: Are My Results Unexpected?