8.7 Skills Focus: Selecting an Appropriate Inference Procedure for Categorical Data
6 min read•june 18, 2024
Jed Quiaoit
Josh Argo
AP Statistics 📊
265 resourcesSee Units
The Most Important Part(s) of Unit 8...
The most difficult and most important part of Unit 8 is being able to select which Chi-Squared test to perform. Be sure to study these important distinctions for clarity on which test to select: 🔎
- Goodness of Fit Test: One sample, one categorical variable with more than two categories
- Independence Test: One sample, two categorical variables with multiple categories
- Homogeneity Test: Two samples, one categorical variable with possible multiple categories
It is very likely that you will see one or two multiple-choice questions on this exact content: selecting an appropriate inference method.
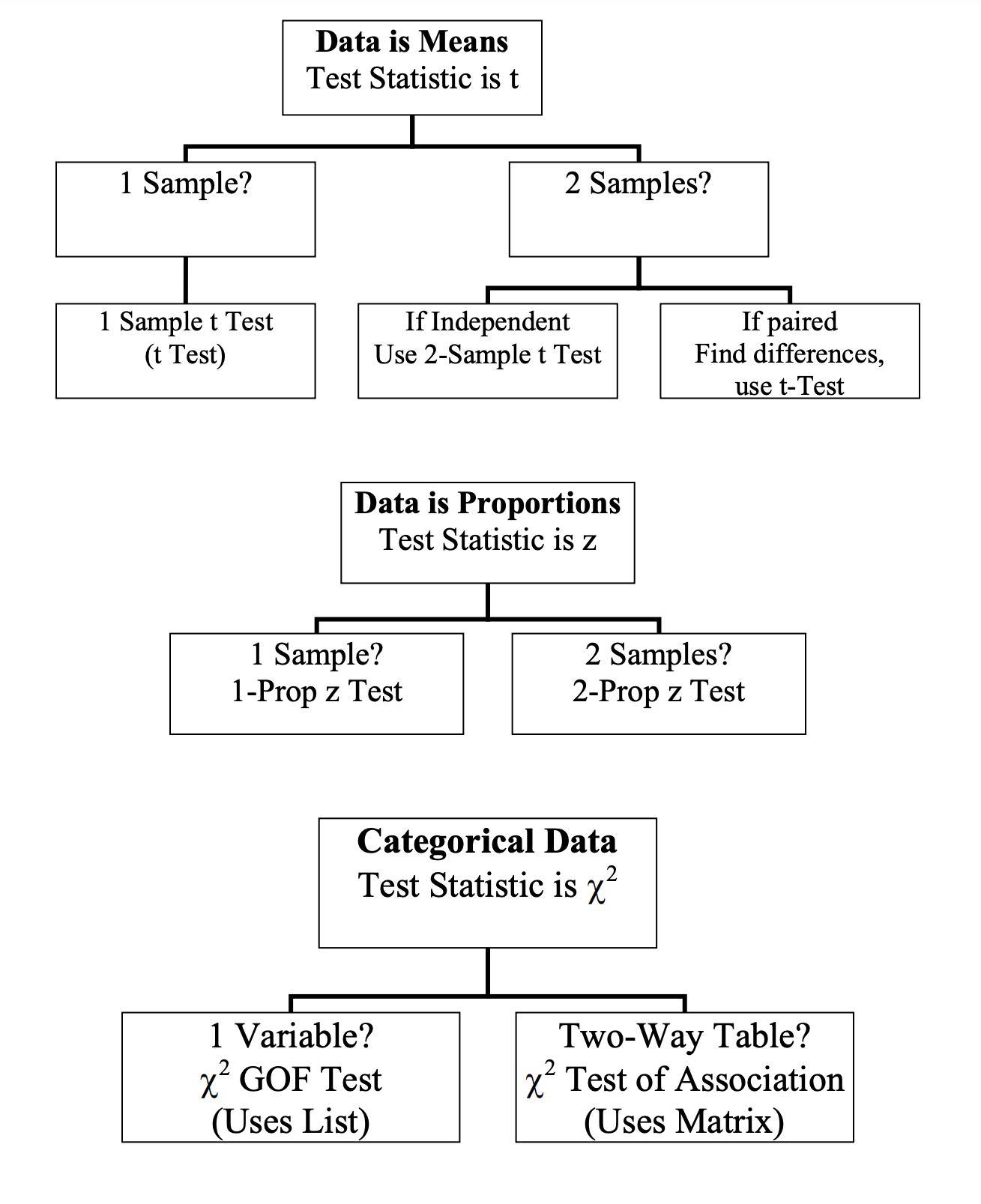
Source: Dan Shuster
Example
On the 2009 AP Statistics exam, the following question was presented in the FRQ section:

Image from released College Board material
The first thing we should notice is that this data is dealing with categorical data. This tells us that we should either use a z-test or a chi-squared test, depending on how many variables and categories we are dealing with. 🤔
Then we notice that there are two categorical variables with two to three categories apiece. This narrows out a z-test since a 1-prop z-test or 2-prop z-test would only be valid if each variable only had two categories. Since we have two variables with multiple categories, this shifts us to a chi-squared procedure.
Now, we are stuck between the three types of chi-squared tests. Uh-oh...
The first thing to notice now is that we have a two-way table, not a one way table with multiple rows/columns so that narrows it down to either chi-squared test for independence or chi-squared test for homogeneity.
The last thing we need to check in narrowing this down is how many samples/populations we have. Since we only took one sample and asked their gender and job experience, this would mean that we are looking at the association between gender and job experience, not the difference in two populations. Therefore, we should run a chi-squared test for independence.
Our hypotheses then should be:
- H0: There is no association between gender and job experience for high school seniors in the district.
- Ha: There is an association between gender and job experience for high school seniors in the district.
Things to remember: be sure to put your hypotheses in context and your null hypothesis is always the “expected” outcome (i.e., there is nothing special going on).
Practice Problem
(1) A researcher is interested in determining whether the distribution of favorite ice cream flavors among college students is the same as the distribution of favorite ice cream flavors among the general population. They survey a random sample of 500 college students and find that 280 students prefer chocolate, 120 students prefer vanilla, 50 students prefer strawberry, and 50 students prefer mint. The researcher also surveys a random sample of 1000 people from the general population and finds that 400 people prefer chocolate, 300 people prefer vanilla, 200 people prefer strawberry, and 100 people prefer mint. The researcher wants to know whether the distribution of favorite ice cream flavors is the same among college students and the general population. 🍨
To answer this question, the researcher plans to conduct a chi-squared test for goodness of fit. However, the researcher is unsure whether a chi-squared test for goodness of fit, homogeneity, or independence is the appropriate test to use.
Which test should the researcher use and why?
(2) A scientist is studying the effectiveness of a new treatment for a particular disease. They conduct a clinical trial with 100 patients and divide them into two groups: a treatment group and a control group. The treatment group receives the new treatment, while the control group receives a placebo. The scientist wants to determine whether the treatment is effective at reducing the occurrence of the disease in male and female patients. 🦠
To do this, the scientist plans to conduct a chi-squared test for independence. However, the scientist is unsure whether a chi-squared test for goodness of fit, homogeneity, or independence is the appropriate test to use.
Which test should the scientist use and why?
(3) A travel company is interested in determining whether the distribution of vacation package choices made by their customers fits a theoretical distribution that they formulated based on previous years' trends in domestic and international travel. The company surveyed 1000 customers and found that 400 customers chose a beach vacation package, 300 customers chose a mountain vacation package, 200 customers chose a city vacation package, and 100 customers chose a rural vacation package. 🚀
The travel company plans to conduct a chi-squared test for independence to answer their research question. However, they are unsure whether a chi-squared test for goodness of fit, homogeneity, or independence is the appropriate test to use.
Which test should the travel company use and why?
Answer
(1) The appropriate test for this situation is a chi-squared test for independence. This is because the researcher is interested in determining whether the distribution of favorite ice cream flavors is the same between two groups (college students and the general population), which is a test of independence.
A chi-squared test for goodness of fit would be used if the researcher was interested in determining whether the observed distribution of favorite ice cream flavors among college students fits a theoretical distribution.
A chi-squared test for homogeneity would be used if the researcher was interested in determining whether the distribution of favorite ice cream flavors is the same among different subgroups within a single population (such as male and female college students).
Therefore, the researcher should use a chi-squared test for independence to determine whether the distribution of favorite ice cream flavors is the same between college students and the general population.
(2) The appropriate test for this situation is a chi-squared test for homogeneity. This is because the scientist is interested in determining whether the distribution of the disease is the same among male and female patients within a single group (the treatment group). A chi-squared test for homogeneity allows the scientist to determine whether there is a difference in the distribution of the disease between male and female patients in the treatment group.
A chi-squared test for goodness of fit would be used if the scientist was interested in determining whether the observed distribution of the disease among the treatment group fits a theoretical distribution.
A chi-squared test for independence would be used if the scientist was interested in determining whether there is a relationship between the treatment (the independent variable) and the occurrence of the disease (the dependent variable).
Therefore, the scientist should use a chi-squared test for homogeneity to determine whether there is a difference in the distribution of the disease between male and female patients in the treatment group.
(3) The appropriate test for this situation is a chi-squared test for goodness of fit. This is because the travel company is interested in determining whether the observed distribution of vacation package choices fits a theoretical distribution. A chi-squared test for goodness of fit allows the travel company to compare the observed distribution with the theoretical distribution and determine whether the two are similar.
A chi-squared test for independence would be used if the travel company was interested in determining whether there is a relationship between two variables (such as the type of vacation package and the destination chosen).
A chi-squared test for homogeneity would be used if the travel company was interested in determining whether the distribution of vacation package choices is the same among different subgroups within a single population (such as male and female customers).
Therefore, the travel company should use a chi-squared test for goodness of fit to determine whether the observed distribution of vacation package choices fits a theoretical distribution.
🎥 Watch: AP Stats Unit 8 - Chi Squared Tests
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.