AP Calculus Free Response Question (FRQ) Overview
10 min read•june 18, 2024
N
Nick Molnar
AP Calculus AB/BC ♾️
279 resourcesSee Units
Overview of the Free-Response Questions (FRQ)
The second component of the AP Exam includes 6 Free Response Questions (FRQs).
You’re given 30 minutes to complete the first two—Part A. These both require a calculator. Then you’ll have 1 hour for the remaining four—Part B. These, however, are tech-free. Not to worry, though, in the sections ahead we’ll detail what you can expect in each part and how to maximize your score.
Speaking of scoring, the AP weights each problem equally, 9 points apiece (more later). And, taken together, this section accounts for 50% of your total exam score.
📖 Content
The AP course emphasizes 3 big ideas: change, limits, and analysis of functions. While the specific content varies from year-to-year, in aggregate the exam will test your ability to understand and interpret functions represented in a variety of forms: graphically, from a table, in written form, and as an equation.
Each FRQ contains 3 or 4 related sub-tasks, and you can expect a fairly even split between process-oriented and conceptual questions.
- Process-Oriented: find the derivative; estimate the value of a definite integral; or identify the location or value of a relative maximum
- Conceptual: interpret the graph of the first derivative, f'; verify the conditions of the Mean Value Theorem (MVT); explain why the rate of change of a system is positive or negative with justification
Note: these lists are not exhaustive, but the FAQs section below discusses other examples
In addition, two questions (at minimum) will feature an authentic scenario. This means they’ll give you more context than an abstract equation or graph.
.png?alt=media&token=8d24d0a0-773b-4386-9461-269c07b1c2e8)
✋ Justification
So what do you need to do differently in the FRQ section? In the words of every math teacher you’ve ever had: show your work.
This emphasis on justification is more than mere suggestion. Approximately half of the points possible depend on your ability to support your answer. Of course, what constitutes good justification depends on the question. See the comparisons below.
.png?alt=media&token=6d698de6-670a-4cfb-ba67-8b6dd4b85c28)
While this is accurate, it isn’t clear that this is the derivative nor how we arrived here. A better answer would include evidence of our process.
.png?alt=media&token=5c6d6946-b93a-481f-ae32-dcd8d58ef886)
Here, we clearly show we’re taking the derivative—using the power rule and the chain rule. If we make an arithmetic error, the reader knows what we were attempting. In these situations you may earn yourself some of the available points. However, if you make a calculation error in the first solution, you’ll earn no points at all.
.png?alt=media&token=0e2823b4-ebe5-46e2-921f-13f6dd442e1a)
Again, technically the result is accurate. Still, we could do much better to communicate our line of thinking.
.png?alt=media&token=02a5969b-df77-458a-8351-b69a6e4e9016)
Step one indicates that we’ve taken the derivative at x=3. Next we show the location of the point of intersection (3, p(3)). Finally, we label our result.
Before we move on, just a few more quick examples.
.png?alt=media&token=fa1d7f61-8db5-4cae-b376-00378e6534dd)
*NOTE: simply providing a +/- chart (a common practice for these types of problems) does not supply sufficient justification. A simple sentence indicating a change, however, will suffice.
💯 Scoring
As mentioned earlier, each FRQ counts equally. Within each sub-question, however the weightings can vary slightly. That said, normally each part counts 2 or 3 points toward the 9 point total. Thus, the maximum possible tally for the entire Free Response Section is 54 points. For reference, the MC section contributes 54 points, as well. Your raw score will sum these two.
If you’re aiming for a 5? The cutoff changes every year, but a general guide is that raw scores above 70 should qualify.
And what about a 4? Here, again, it varies year-to-year. Usually, raw scores between 60-69 will translate to a 4.
Earning Points
AP readers—those people you’re trying to please with your answers—award points based on accuracy and on completeness. To earn maximum marks you’ll need both.
Above, we discussed some particulars of how to justify your answers. It’s important because they contribute significantly to your total score.
That said, you will earn points for other things. You’ll earn points for setting up derivatives and integrals properly; using complete and proper notation; logically moving step-by-step through your mathematical process; and providing the correct answer with the corresponding units, where appropriate. So, what does this look like?
♾️ Derivatives
.png?alt=media&token=d1825111-dd84-4253-8be8-1654d26a2810)
♾️ Integrals
.png?alt=media&token=6d68894c-c6d5-49f4-8f97-db9047a766dc)
.png?alt=media&token=8c18f7ed-dbdf-40c8-ab4b-dbac4285c579)
♾️ New Representation
.png?alt=media&token=cf0e5e09-fd16-4532-9e51-53317b549996)
♾️ Appropriate Units
- Rates: At t = 3, the rate at which people are leaving is 142 every hour.
- Average: On [3, 7] the average rate of change of v is 6 meters/sec.
- Accumulation: The liquid has cooled 8 degrees Fahrenheit over the interval from t = 0 to t = 15 mins.
Part A - Calculator Section
2 Questions; 30 minutes; Graphing Calculator Needed; Justification also needed
Exactly what do they mean when they say calculator required?
Well, you can expect to be asked to graph gnarly functions. They often won’t give you a useful window, so you’ll also need to find that. In these scenarios, try the ZoomFit option. It isn’t always perfect, but it can be a lifesaver and (at minimum) point you in the right direction. This is usually just a first step.
Often the questions ask you to find zeros (keep at least 3 decimal places) or locate relative (or absolute) minimums and maximums.
Remember, if they ask for location, they're looking for the x-coordinate.
- f(x) achieves a local minimum at x=6.374 because f'(x)=0 here and f'(x) changes sign from negative to positive.
And if they ask for the absolute maximum? Then they want the y-value.
- g(6) = 123 is the absolute maximum value, as it’s greater than the value of gat both endpoints: g(0)=100 and g(8) = 74.
What else is your calculator good for? Calculating! The AP also may ask you to compute the value of a first or second derivative at a specific point. Similarly, they could ask for the numerical value of any type of definite integral. Need to practice? We’ve got you covered.
OK. But how am I supposed to justify? I’m glad you asked. Let’s look at an example.
📖 Worked Example
A local citrus vendor stocks her stand with 100 pounds of clementines at 9 a.m, at which time the market opens. She leaves her partner in control of the stand and returns to the farm to pick up more fruit. Customers buy her fruit at a rate of
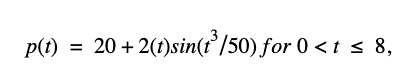
where p(t) is in pounds and t is the number of hours since 9 a.m. Three hours later, the vendor returns with a resupply and moves them from the truck to the stand at a rate modeled by
.png?alt=media&token=afa94b60-43ad-4b4d-a4c1-ce8a45c7c53a)
.png?alt=media&token=e3f57898-894e-4b0e-9a26-34cba18dad0f)
.png?alt=media&token=2ad04dcf-c1d6-4013-a58d-4bff4abdd1d7)
.png?alt=media&token=a2376fdd-9e28-439c-a1d3-789e1050f5de)
.png?alt=media&token=223db7a5-3222-4df6-9c41-e9f3648d7dde)
And there you have it! In Part A, you’ll lean heavily on your calculator. And as long as you provide good, clear mathematics notation, appropriate reasoning, and correct units, you’ll be prepared to collect maximum points!
📊 Past Trends
Many AP Calculus teachers attempt to predict the types of FRQs that will appear on the upcoming exam. As you’ll see below, Modeling Rates and Particle Motion have been popular in the past few years.
2019: Modeling Rates and Particle Motion
- 1—integrate a difference of rates (definite); average value calculation (not average rate of change); find maximum; interpret rate of change (of a rate)
- 2—from a table, justify intermediate value theorem (IVT); approximate using trapezoidal rule; compute distance traveled given velocity; calculate a relative distance between two moving bodies
2018: Modeling Rates and Particle Motion
- 1—definite integral given a rate and bounds; integral evaluation with constant function adjustment; finding zeros; minimize a difference of functions
- 2—find and calculate derivative; evaluate a definite integral with initial condition; interpret displacement vs. total distance traveled
2017: Modeling Volume/Related Rates and Modeling Rates
- 1—Riemann sums approximation from a table; determine over/underestimate with justification; modeling volume from an equation given cross-sectional heights; applying the fundamental theorem of calculus (FTC)
- 2—compute a definite integral given a rate and bounds; calculate and interpret the derivative of a rate; find and explain the difference of two rates; compute a definite integral with an initial condition
📱 A Note on Calculators
Above all, whichever calculator you select, make sure you’re familiar with it. It’s useful to refresh (and practice!) the calculator functions you’ll need on exam day.
In short, you’ll need a graphing calculator for the exam. And while you’ve likely used one all year that falls within the guidelines, the AP is quite particular about which graphing calculator model you may use.
You are permitted to bring a backup calculator, though if you’re using fresh batteries and pack a few extras (just in case) you should have plenty of insurance.
Graphing Calculator Models (as of October 2019) | |
Texas Instruments | TI-73; T1-80; TI-81; TI-82; TI-83 (Plus and Plus Silver) TI-84 (Plus/CE, Plus Silver, Plus C Silver, Plus T, Plus CE-T) TI-85; TI-86; TI-89 and Titanium TI-NSpire (CX, CX II, CX II-T) TI-NSpire (CX II CAS, CX II-T CAS, CX II-C CAS) |
Casio | FX-6000 Series; FX-6200 Series; FX-6300 Series FX-6500 Series; FX-7000 Series; FX-7300 Series FX-7400 Series; FX-7500 Series; FX-7700 Series FX-7800 Series; FX-8000 Series; FX-8500 Series FX-8700 Series; FX-8800 Series; FX-9700 Series FX-9750 Series; FX-9860 Series; FX-CG-5000 (No Stylus) FX 1.0 Series; FX-CG-10; FX-CG-20 Series; FX-CG-50 CFX-9800 Series; CFX-9850 Series; CFX-9950 Series CFX-9970 Series; Algebra FX 2.0 Series Graph25 Series; Graph35 Series; Graph75 Series Graph95 Series; Graph100 Series |
HP | HP-9G; HP-28 Series; HP-38G; HP-39 Series; HP-40 Series HP-48 Series; HP-49 Series; HP-50 Series; HP Prime |
Radio Shack | EC-4033; EC-4034; EC-4037 |
Sharp | EL-5200; EL-9200 Series; EL-9300 Series EL-9600 Series (No Stylus); EL-9900 Series |
Other Models | Datexx DS-883; Micronta; NumWorks; Smart² |
Part B - Non-Calculator Section
4 Questions; 60 minutes; Graphing Calculator Prohibited
Alas, you’ll need to put away your trusty TI (or other approved model) in the final section of the exam. Looking for consolation? Well, on a number of the problems your calculator wouldn’t offer much help or time-savings anyway. How could that be?
Here the AP likes to test your ability to interpret graphs, tables, and slope fields.
What can you discern about g''(t)at t=a if you’re given a picture of g(t)?
Use a table of f(t)values to guarantee the existence of a particular f'(t) value.
Could you produce a specific solution to a differential equation from a slope field?
These examples should give you some idea, but for clarity let’s work an example.
📖 Worked Example
.png?alt=media&token=1682c367-4572-4850-ad15-7abbda031681)
The function g is differentiable on the closed interval [-6, 3]and satisfies g(-2) = 15. The graph of g' consists of a semicircle, a line segment, and a quarter-circle, as shown above, where g'(2) = 1.
.png?alt=media&token=081bb66b-76ce-4207-a70a-880fd05cac76)
.png?alt=media&token=d4e70832-7ecf-4414-bc2c-224f25bdb161)
.png?alt=media&token=acca4e48-be7f-4e7a-9955-c46e9f297ebf)
.png?alt=media&token=b56989fb-f56b-4dc4-b15e-2cde5304cf04)
Congratulations! Once you complete Part B, you’ve completed your exam. On test day remember to use good, clear mathematics notation, and always justify your answer!
📊 Past Trends
As mentioned earlier, it’s a popular pastime of some AP Calculus teachers to predict the content that will appear in the upcoming FRQs. You’ll notice that a problem requiring you to analyze a graph and apply FTC has appeared with some frequency.
2019
- Graphical Analysis of f and application of FTC
- Modeling using Separable Differential Equations
- Calculating Area and Volumes of Revolution
- Function Analysis—L’Hospital and Squeeze
2018
- Graphical Analysis of f' and application of FTC
- Modeling from a table of data and analytically
- Function Analysis—L’Hospital
- Separable Differential Equation including Slope Fields
2017
- Graphical Analysis of f' and application of FTC
- Modeling using Separable Differential Equations
- Particle Motion
- Function Analysis from a table of data and graphically
FAQs About FRQs
We’re not done quite yet. Here’s a final reference for things we may not have covered above.
Q: I made a mistake, should I erase it?
A: If it’s minor, sure. With more significant mistakes, however, it’s quicker and clearer to cross out your work. You can always point the reader forward with an arrow.
Q: What if I found two solutions and I’m not sure which is correct?
A: Ideally, you’ll have a hunch one way or the other and you’ll clearly identify that answer. If you’re flummoxed, though, or you run out of time, here’s what’s likely to happen. Readers will usually score both solutions, take the arithmetic mean, and then round down. You won’t earn your top score, but it’s possible you may earn more points. As we’ve seen though, with good justification, you can overcome an errant final answer.
Q: Do I have to round my answers to 3 decimal places?
A: Unless the question specifies specific rounding (usually this is to the nearest integer), you won’t be penalized if you leave more than 3 correct places.
Q: Can use the nDeriv notation my calculator uses?
A: No. Stick to proper mathematics notation: f'(x) or ddx
Q: If a question doesn’t ask me to justify or show my work, do I need to?
A: Answers always require justification to receive full marks. Just justify it.
Q: What happens if I make an error in part (b) and need to use my answer in part (c)?
A: Here, the reader is on your side. You shouldn’t be penalized for carrying an incorrect value from a prior part of the question. Your reader will score your answer differently. Usually, she will re-compute the sub-question with the erroneous input. If your process and justification are correct, you’ll earn the corresponding points.
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.