AP Calculus AB/BC ♾️
279 resourcesSee Units
Answers and Review for Multiple Choice Practice on Differentiation: Definition & Fundamental Properties
⛔STOP!⛔ Before you look at the answers make sure you gave this practice quiz a try so you can assess your understanding of the concepts covered in unit 2. Click here for the practice questions: AP Calculus Unit 2 Multiple Choice Questions.
Facts about the test: The AP Calculus exam has two sections of multiple choice: 30 questions in 60 minutes with no calculator, and 15 questions in 45 minutes with a calculator.
*The following questions were not written by CollegeBoard and although they cover information outlined in the AP Calculus Course and Exam Description the formatting on the exam may be different.
1.
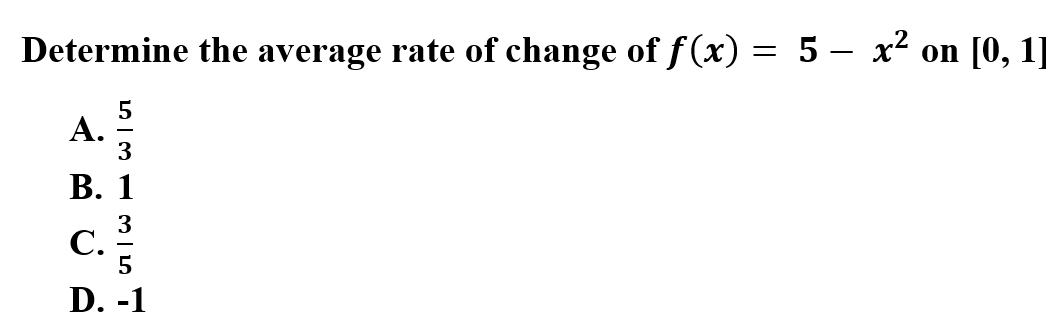
Explanation: D is correct because to find the average rate of change, you will take the interval and plug into the function. This will allow you to determine the y-coordinate, then you can substitute the information into the average rate of change formula.
2.

Explanation: C is correct because the instantaneous rate of change represents the slope of the tangent or the derivative. It can also be represented by the limit of the average rate of change.
3.
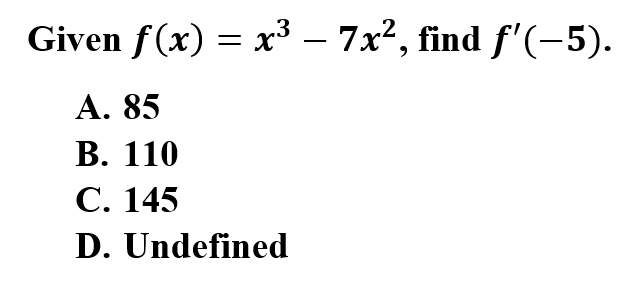
Explanation: C is correct because the derivative at a point can be found by finding the slope at that point. Take the derivative of f(x) using the power rule and substitute into the derivative for the given value.
4.

Explanation: B is correct because the derivative represents the slope of the tangent line and the point is given as (5, -2). Take this information and plug into point-slope form.
5.

Explanation: A is correct because the slope of the tangents can be obtained by plugging the two given points into the slope formula. This is also the formula of a derivative.
6.
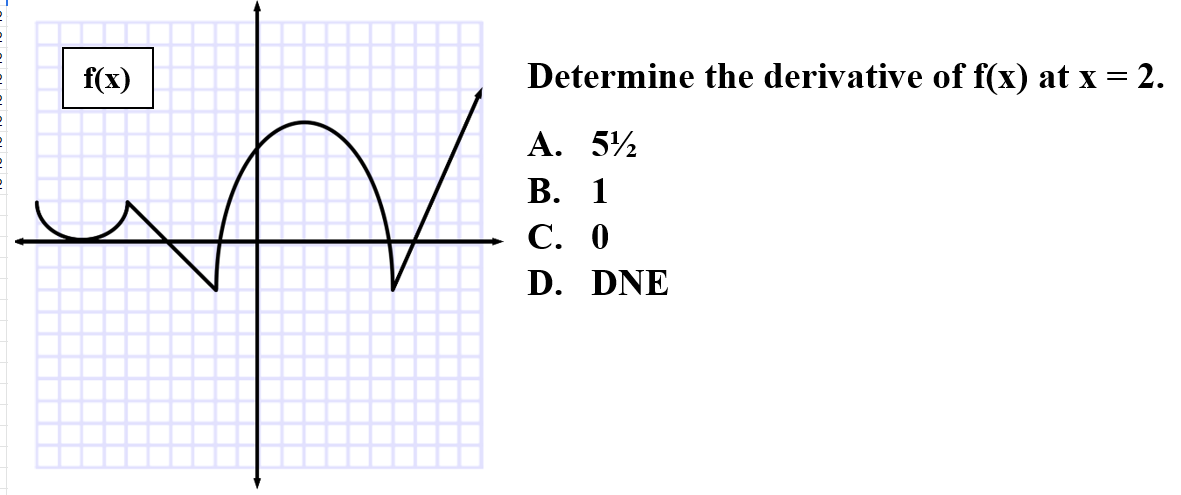
Explanation: C is correct because the derivative at maximums are horizontal tangent lines. Horizontal lines have a slope of 0.
🎥 Watch: Introduction to Finding Derivatives
Explanation: B is correct because first you will need to rewrite the fraction with a negative exponent. Using the power rule for derivatives, multiply the constant by the exponent and subtract 1 from the exponent. Do not forget to simplify.
🎥 Watch: Introduction to Finding Derivatives
8.
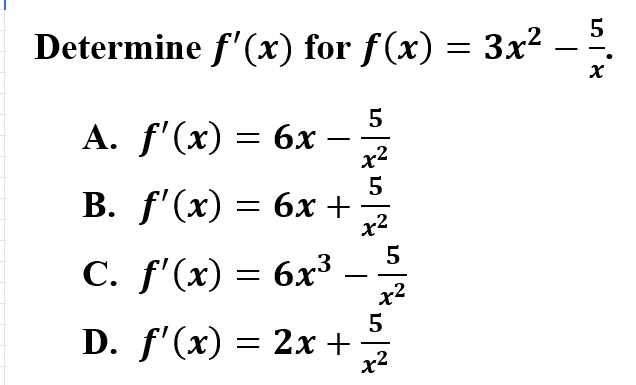
Explanation: B is correct because first you will need to rewrite the fraction with a negative exponent. Using the power rule for derivatives, multiply the constant by the exponent and subtract 1 from the exponent. Do not forget to simplify.
📄 Study Unit 2.5: Applying the Power Rule
9.
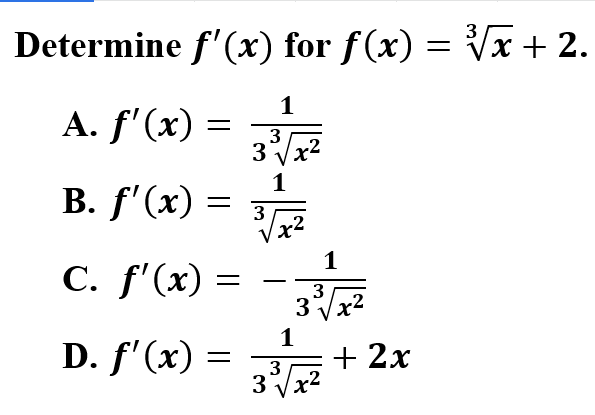
Explanation: A is correct because first you will need to convert the radical to an exponent. Using the power rule for derivatives, multiply the constant by the exponent and subtract 1 from the exponent. Do not forget to simplify.
📄 Study Unit 2.5: Applying the Power Rule
10.
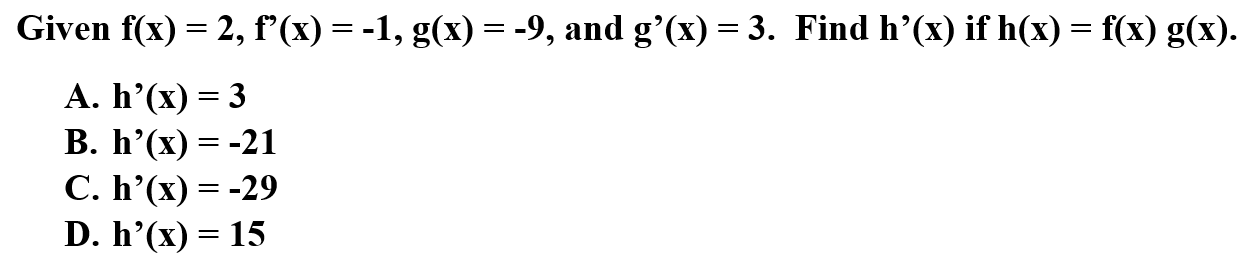
Explanation: D is correct because to determine h'(x), you must utilize the product rule. The product rule consist of f'(x) g(x) + f(x) g'(x).
📄 Study Unit 2.8: The Product Rule
11.
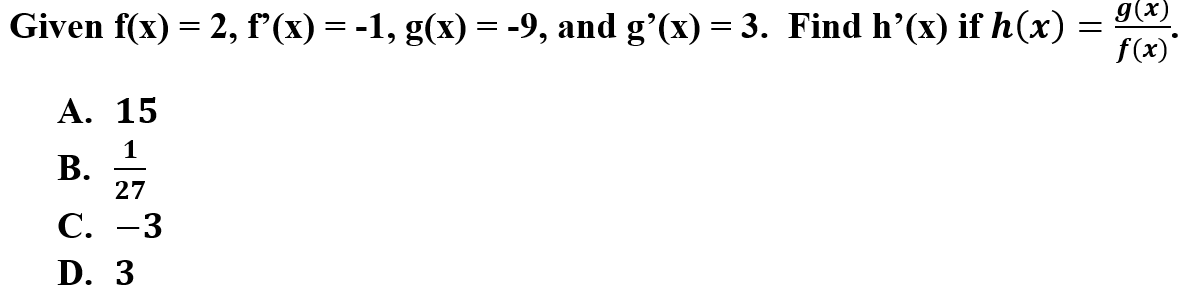
Explanation: C is correct because to determine h'(x), you must utilize the quotient rule. The quotient is f(x) g'(x) - g(x) f'(x) all divided by f(x) squared.
📄 Study Unit 2.9: The Quotient Rule
12.
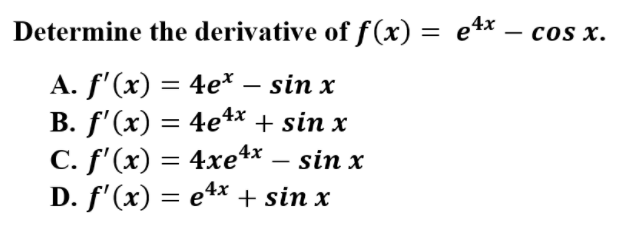
Explanation: B is correct because the derivative utilizes the power rule and the rules for exponential and trigonometric functions. Be sure to keep e intact and change the sign with the derivative of cos x.
13.
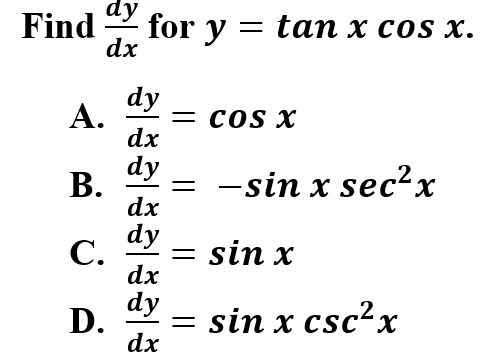
Explanation: A is correct because taking the derivatives of trigonometric functions requires you to understand/memorize the derivatives of trigonometric functions. In some cases (like this one), you may be able to simplify before taking the derivative to make it a less complicated derivative.
14.

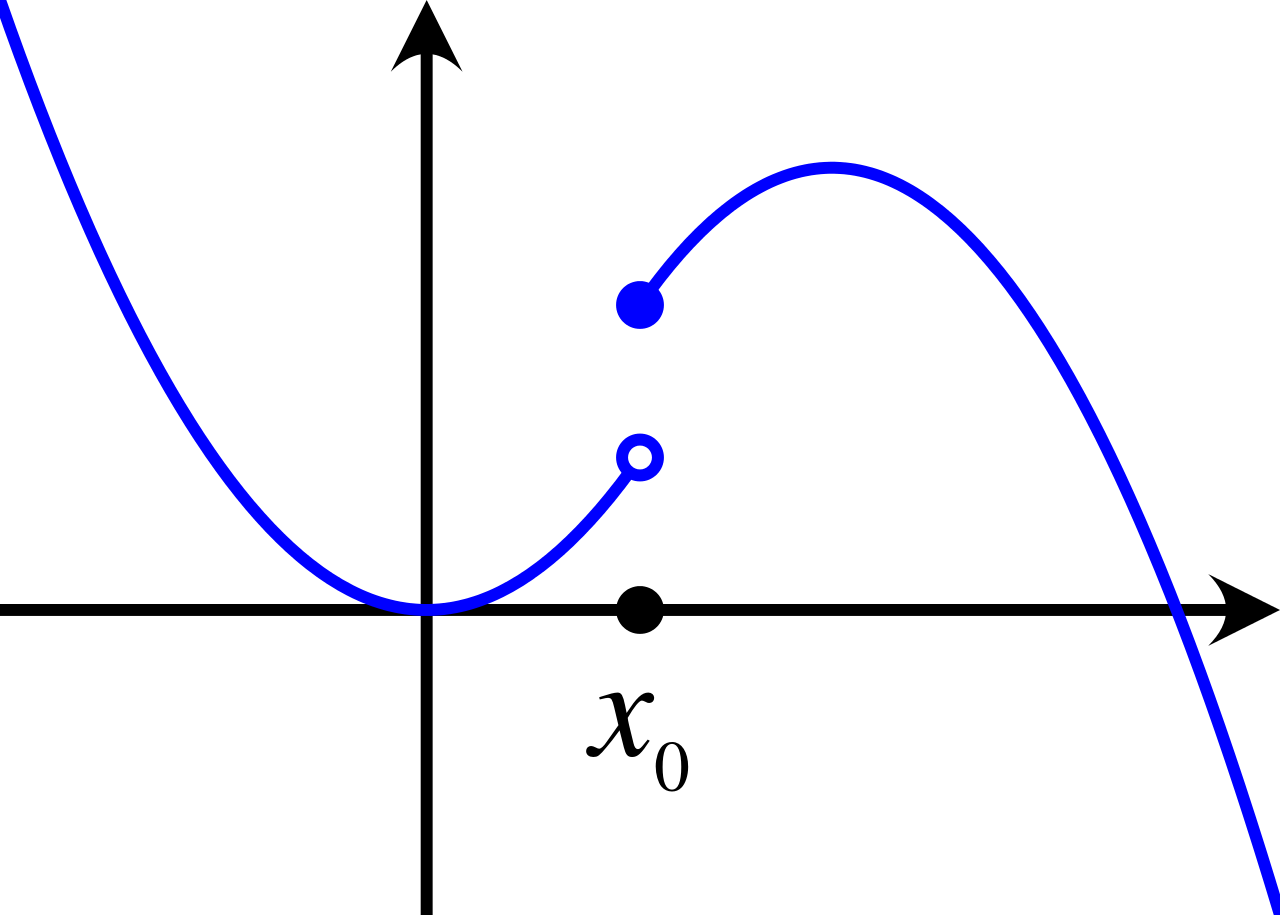
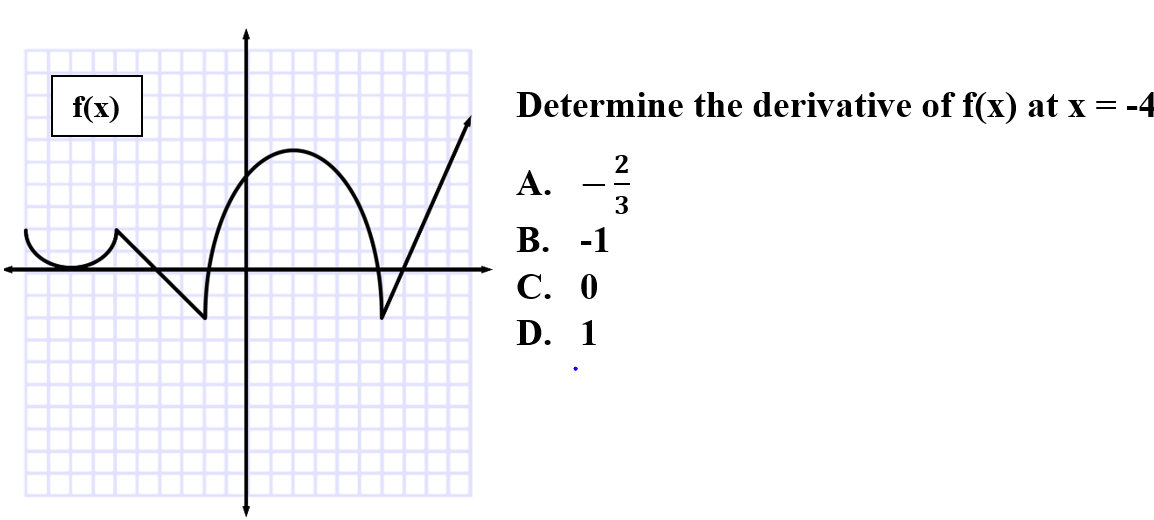
Explanation: D is correct because when a function has a sharp corner or turn, is not continuous, and/or has a vertical tangent line it is not differentiable. These are the special case for nondifferentiability.
📄 Study Unit 2.4: Connecting Differentiability and Continuity: Determining When Derivatives Do and Do Not Exist
15.

Explanation: B is correct because the function f(x) passes the tests for continuity. Also, the function does not create a sharp turn nor a vertical asymptote at a. Therefore, the function is continuous and differentiable.
📄 Study Unit 2.4: Connecting Differentiability and Continuity: Determining When Derivatives Do and Do Not Exist
What can we help you do now?
🤝Connect with other students studying AP Calculus with Hours
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
🧐Multiple Choice Questions (MCQ)
✍️Free Response Questions (FRQ)
📆Big Reviews: Finals & Exam Prep

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.