Unit 3 Overview: Differentiation: Composite, Implicit, and Inverse Functions
2 min read•june 14, 2021
Jillian Holbrook
AP Calculus AB/BC ♾️
279 resourcesSee Units
Exam Weighting ⚖
Calculus AB: 9–13%
Calculus BC: 4–7%
Developing Understanding 🧠
Unit 3 builds upon understanding from Unit 1 and Unit 2 of AP Calculus. The two main components of Calculus are differentiating and integrating. Of these two, differentiation is the focal point of the first few units in Calculus.
This unit, in particular, emphasizes the analysis of functions, continued correct application and understanding of function notation, and the recognition of “inner” and “outer” functions within composites. This unit makes up 9-13% of the Calculus AB exam and 4-7% of the Calculus BC exam.
This list will be a good place to start in terms of self assessing what you need to study or learn. As you are looking through this list write down what topics on this list you don’t remember or still need to learn. Go to the full study guide page then for this topic to get some more information!

Image Courtesy of Giphy
Main Topics and Sections:
Chain Rule (3.1)
Use when you are deriving a function that is a composition of functions:

Implicit Differentiation (3.2)
Use when you have an equation that looks like this:
3xy + 2y = 50x
*The first step would be to differentiate with respect to x*
Differentiating Inverse Functions (3.3)
Use this formula to help find the derivative of the inverse function:
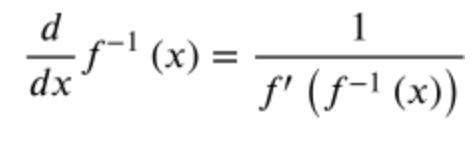
Differentiating Inverse Trig Functions (3.4)
Memorize these to help you solve problems quickly and efficiently!
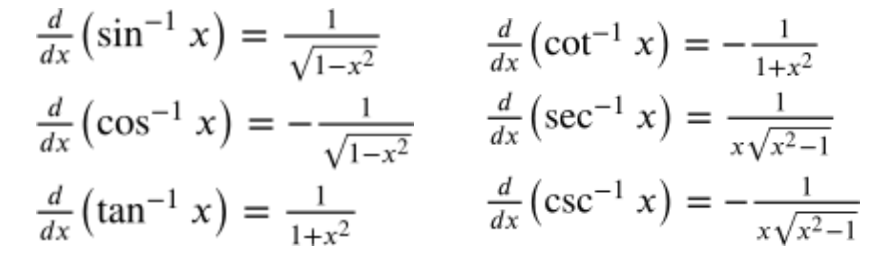
Selecting Procedures for Calculating Derivatives (3.5)
When you are selecting procedures for calculating derivatives decide if the function you are looking at is:
- A composition of functions
- for example:
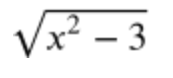
- Two functions multiplied together
- for example:
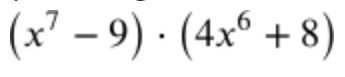
- Two functions divided
- for example:
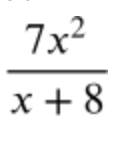
- A function with exponents
- for example:

A function with trig in it
for example:

Calculating Higher Order Derivatives (3.6)
When you get into the next few units you will need to take the next derivate; especially when you get into describing functions and finding where it is increasing, decreasing, concave up and concave down.
The notation for the derivatives are:
- f’(x): First derivative
- f’’(x): Second derivative
- f’’’(x): Third derivative
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
🧐Multiple Choice Questions (MCQ)
✍️Free Response Questions (FRQ)
📆Big Reviews: Finals & Exam Prep

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.