4.4 Intro to Related Rates

2 min read•june 11, 2020

Meghan Dwyer

AP Calculus AB/BC ♾️

279 resources

See Units

🎥Watch: AP Calculus AB/BC - Related Rates

What are Related Rates?

Related Rates are exactly what they sound like. It is using formulas and expressions that we know involve the same variables to find missing rates. These problems can look very different but are really following a similar process. 💻

The Process 📠

Draw a picture! Assign variables to anything you have or need to find, and label the picture as so.
Find out which rates you know, and which rates you are looking for. Label them using the variables you used in part 1 as derivatives. Make sure it is with respect to time!

Ex. If you labeled a ladder length c, and you know the rate at which the length of the ladder is changing, then you should label that rate dc/dt.

Find an equation that relates to what you are looking for and what you already know. (This will not have derivatives in it yet!)
If there is a variable that you do not know the derivative to and you do not need to find the derivative to, plug that known value in right away!
Take the derivative of both sides of the equation.
Plug in what you know and solve for what you do not.

** Don’t forget units! 📌

Example Problem:

A 10-ft ladder is leaning against a house on flat ground. The house is to the left of the ladder. The base of the ladder starts to slide away from the house. When the base has slid to 8 ft from the house, it is moving horizontally at the rate of 2 ft/sec. How fast is the ladder’s top sliding down the wall when the base is 8 ft from the house?

Draw a Picture

We can model this as a right triangle with a hypotenuse 10 and legs x and y:

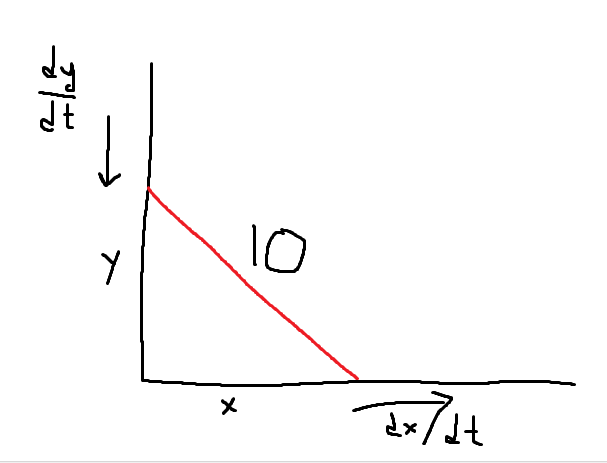
Note that dy/dt and dx/dt are the rates of change of the lengths of the triangle with respect of time. They are the rate at which the ladder is sliding in either direction.

Equation to Relate

With rights triangles, we typically like to use the Pythagorean Theorem. Trying this we find that x^2 + y^2 = 100. Deriving with respect to time we find that 2x dx/dt + 2y dy/dt = 0.