6.14 Selecting Techniques for Antidifferentiation (AB)
6 min read•june 18, 2024
AP Calculus AB/BC ♾️
279 resourcesSee Units
Review of integration techniques
- Integrating using substitution: When an integrand can be rewritten temporarily to produce an integrandsimpler to integrate. We must return back to the original integrand once we’ve integrated. When is substitution mostly used? When an integrand is comprised of both a function and it’s a version of its own derivative! Think Chain Rule!
- Integrating using long division: used to integrate a rational expression whose numerator’s degree is either greater than or equal to its denominator’s degree. When this occurs, always use an algebraic technique called polynomial long division first.
- Integrating by completing the square: Completing the square helps when quadratic functions are involved in the integrand.
Of course, there are more techniques for AP Calc BC, so if you're looking for help with those topics, check out 6.11-6.13 labeled BC only.
Let's review key features of problems that will help you determine which technique to use!
Integrating using substitution
In order to integrate using substitution, you need to have both a function and its derivative present. You have a "u" function and a "du" function, where "u" is the function and "du" is its derivative.
**Tips to finding a “good” u:
- Typically u will be an “inside” function
- du or something that appears considerably similar to du will be present in the integrand as well
- If you have an expression that is a fraction with a polynomial in the denominator, substitution can often help you integrate the fraction.
- If you have an expression that contains a square root or other radical, substitution can often help you rewrite the expression
- If you have an expression that contains an absolute value, substitution can often help you rewrite the expression
- If you have an expression that contains a logarithm, substitution can often help you rewrite the expression
- If you have an expression that contains an inverse trigonometric function, substitution can often help you rewrite the expression
- If you have an integral that involves a trigonometric substitution, substitution can help you rewrite the integral
Let's Practice:
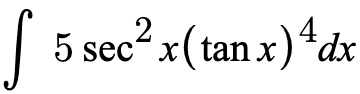
The expression above can be solved using substitution. So we must pick a function for our u and for du
We can see that there is a function tanx and its derivative sec^2(x) so we can pick these values for u and du.
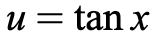
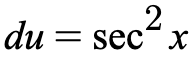
Now that we have our values, we can substitute in the variables to the original integrand and continue with our integration process.
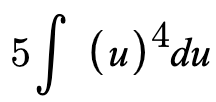
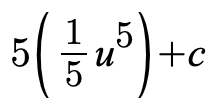
Now we can substitute u back in to get a final answer of:
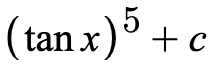
Integrating Using Long Division
We want to integrate with long division when the degree of the function in the numerator is greater than or equal to the degree in the denominator.
Let's review some tips before we practice
- Use long division to divide the polynomial in the integrand by the polynomial in the integrator.
- Identify the remainder after dividing the integrand by the integrator.
- Substitute the result of the long division into the indefinite integral.
- Evaluate the indefinite integral using the fundamental theorem of calculus.
- Pay attention to the signs of the terms in the integrand and the integrator, as this can affect the sign of the remainder.
- Use the properties of logarithms to simplify the result of the long division, if necessary.
- Use the quotient rule for integration to evaluate the integral if the integrand is a quotient of polynomials.
Now, let's practice using long division to integrate!
The following integrand can be solved by using long division because the highest degree in the numerator is greater than the highest degree in the denominator.
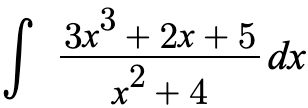
We will use the basic principles of long division:
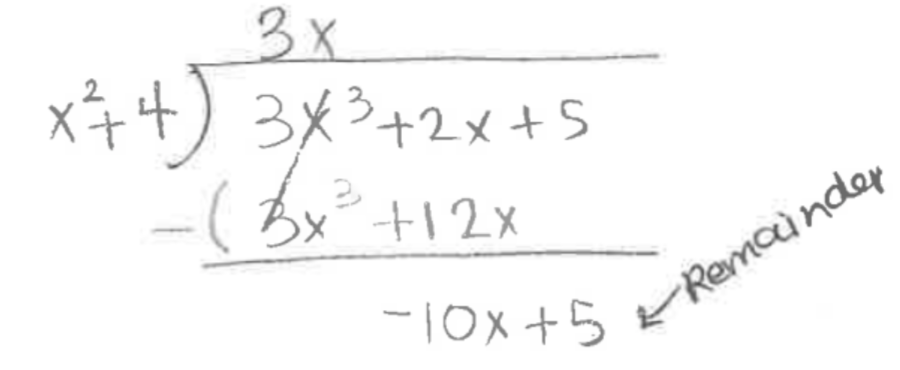
Now we have transformed the original expression into the following
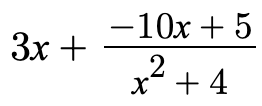
This is much easier for us to split up and integrate. So, we will make three separate integrals since one of the properties of integrals allows us to split them up to solve on their own and add them together at the end.
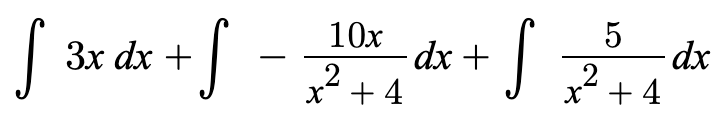
For the first integral, we can simply use the power rule. For the second one, we can use U substitution since we have a function x^2 and its derivative x present. For the final integral, we can use the special derivative of arctan to plug in the values. This leaves us with a final answer of:
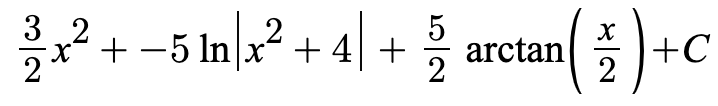
Integration by Completing the Square
We want to use integration by completing the square when a quadratic function is involved in the integrand.
When can you integrate by completing the square?
- If you have an integral that involves a quadratic polynomial
- If you have an integral that involves an expression of the form (ax^2 + bx + c)^n, where n is a positive integer
- If you have an integral that involves an expression of the form (ax^2 + bx + c)^(1/2)
- If you have an integral that involves an expression of the form (ax^2 + bx + c)^(1/n), where n is a positive integer other than 2
- If you have an integral that involves an expression of the form (ax^2 + bx + c)^m, where m is a fraction
- If you have an integral that involves an expression of the form (ax^2 + bx + c)^m, where m is a negative integer
- If you have an integral that involves an expression of the form (ax^2 + bx + c)^m, where m is a negative fraction
- If you have an integral that involves an expression of the form (ax^2 + bx + c)^m, where m is a positive fraction
- If you have an integral that involves an expression of the form (ax^2 + bx + c)^m, where m is a positive integer, you can use integration by completing the square to evaluate the integral.
Let's practice!
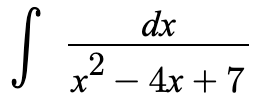
This integrand involves a quadratic expression in the denominator, so we can complete the square to help us integrate.
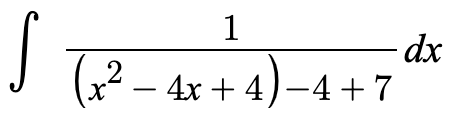
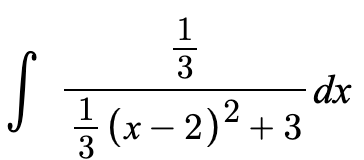
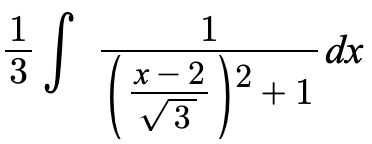
Now, this equation represents the special derivative for arctan!
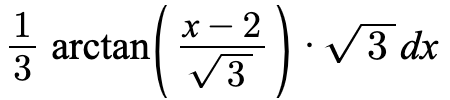
We can simplify our final answer to be:
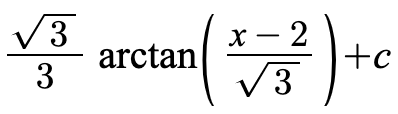
Practicing choosing the right technique
The following expressions can all be solved using one of the three techniques or through power rule. Practice choosing a technique and justifying why that technique would be the most efficient.
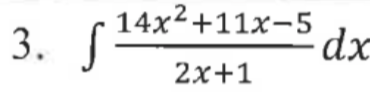
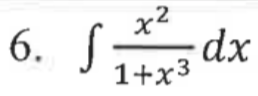
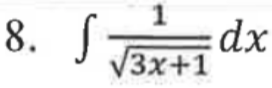
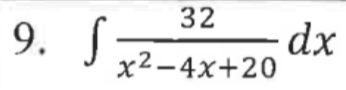
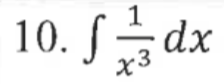
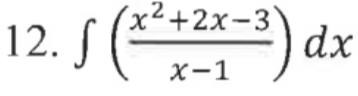
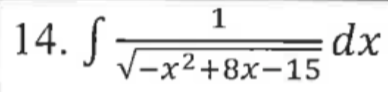
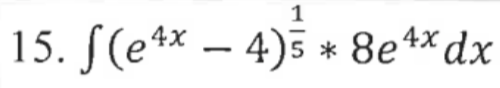
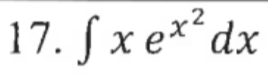
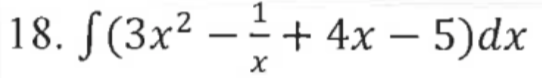
Answers
3. Long division. This integrand has a higher degree in the numerator than in the denominator so using long division would be the easiest process for integration.
6. Substitution. There is a function and its derivative present with x^3 and x^2 so we can use u substitution to integrate
8. Power rule + chain rule. We can use power rule and chain rule to undo the square root and then integrate
9. Completing the square. We can complete the square in the denominator and use the special derivative for arctan.
10. Power rule. We can use a negative exponent to use power rule and integrate.
12. Long division or simplification. In this example, we can use long division to solve, but it could be easier to factor the numerator and cancel the like terms.
14. Completing the square. This one looks scary, but you can use the same process to complete the square, this time with a negative leading coefficient. Instead of using the special derivative for arctan, we will use the special derivative for arcsin to integrate.
15. Substitution. Again, we have a function and its derivative present, so we can use u substitution, with e^4x - 4 and e^4x
17. Substitution. In this instance we have our inside function as u (x^2) and our outside function as du (x). so we can use u substitution to integrate
18. Power rule. We can use power rule for this example since there is no other technique to make it simpler.
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.