Unit 6 Overview: Integration and Accumulation of Change
21 min read•june 18, 2024
Kashvi Panjolia
AP Calculus AB/BC ♾️
279 resourcesSee Units
Introduction
Now that you have mastered derivatives, it’s time to explore another major concept in calculus, the integral. In our study of derivatives, we learned that the graph of a derivative shows the rate of change of the function. If we find the area between such a graph and the x-axis, that area gives the accumulation of change for the function, or the net change. To calculate this accumulation of change, we’ll use basic geometry area skills: rectangles, circles, triangles, and trapezoids. On both the AP Calculus AB and AP Calculus BC exam, this unit makes up 17-20% of the test, so be sure you have a good understanding of these concepts.
This guide is quite long, but provides thorough explanations and examples. Be sure you have a pencil and paper handy so you can follow along to get the most out of it! 📝
6.1: Exploring Accumulations of Change
Let’s say we have a function, g(x), which has a derivative, f(x), as shown below.

To find
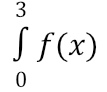
we will add up the area between the derivative graph and the x-axis over the interval from 0 to 3 (the lower number on the integral symbol defines the starting point).
The region from x = 0 to x = 1 is a quarter of a circle with a radius of 1. That means it has an area of π/4. However, we have to be mindful of the sign of the areas when evaluating integrals this way. As we move along the x-axis to the right, the sign of the x-portion of the area is positive. If the derivative graph is below the x-axis, the y-portion of the area is negative. In this case, our answer should be -π/4 because positive (x-portion) times negative (y-portion) is negative. Similarly, from x = 1 to x = 3 we have a right triangle. Our x-portion is positive and our y-portion is negative. Using the formula for the area of a triangle we have 12(2)(-1)= -1. Adding this to the area from the previous interval, we have
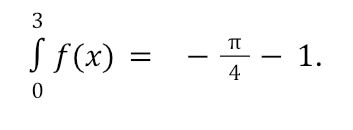
If we move to the left along the x-axis, the x-portion of the area becomes negative. If the derivative graph is above the x-axis, the y-portion of the area is positive. For example, to find
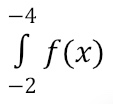
the x-portion of the trapezoid area is negative, and the y-portion is positive.

Note About Units: The units for this type of accumulation problem can be found by multiplying the units for y by the units for x.
6.2 Approximating Areas with Riemann Sums
Another way to approximate the area under a curve (i.e., an integral), is to use the area of rectangles or trapezoids using something called a Riemann Sum. Let’s say we have the function, f(x), graphed below.
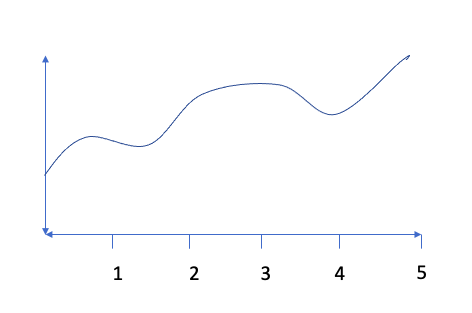
The true value of
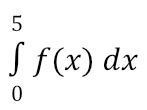
would give us the exact area under the curve (between the function and the x-axis). However, we are unable to use the geometric shapes we used in the previous section to find this exact area. That’s where Riemann comes in handy!
There are 4 different types of Riemann Sums: right, left, mid-point, and trapezoid. These types of problems specify how many sub-intervals to use (i.e., how many rectangles or trapezoids to create). For this example, let’s assume we are asked to use 5 equal subintervals to estimate the value of
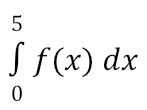
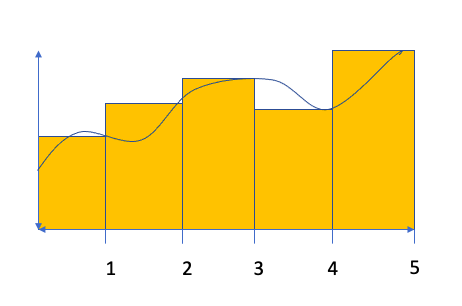
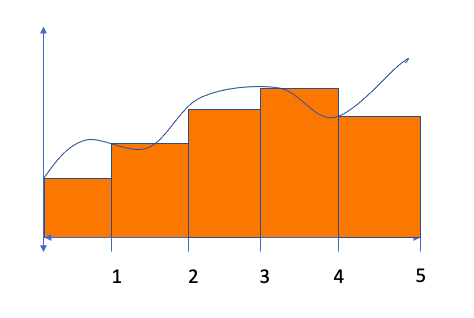
For a right Riemann Sum, we would create five equally-sized bases for rectangles using x-lengths of 1 (e.g. the length from 0 to 1 would be the base of the first rectangle). Then, we would create the height of each rectangle by finding the value of f(x) for the right side of each rectangle as shown below. Notice that some of our rectangles will overestimate the area while others will underestimate the area. The Riemann Sum comes from adding up the area for all of the rectangles. In this case
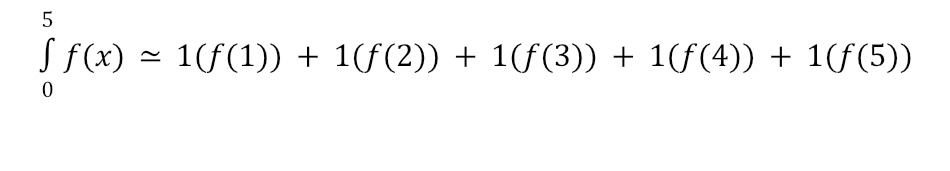
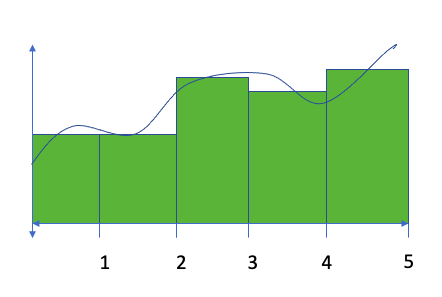
For a Left Riemann Sum, we’ll repeat the process, but use the left side of each rectangle to establish the height, as shown below. This results in the following estimate:
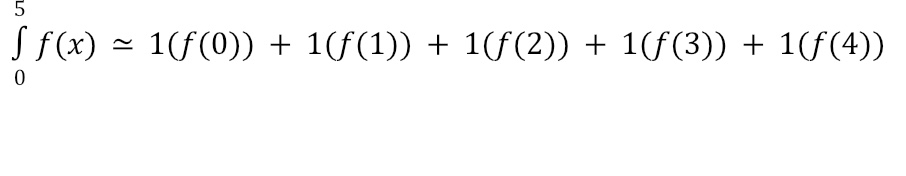
For a Midpoint Riemann Sum, we’ll find the height of each rectangle by using the height for the middle of each base as shown below. This results in the following estimation:
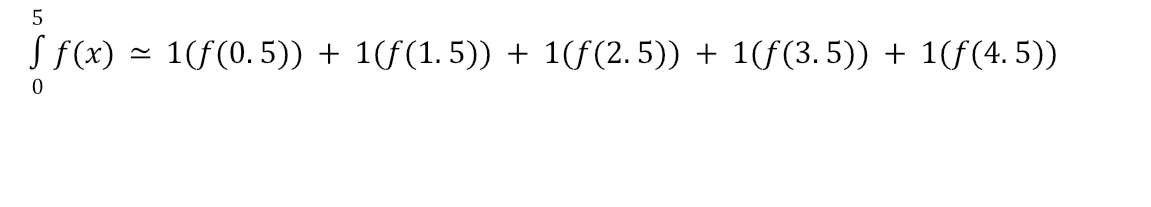
The final Riemann Sum is a trapezoidal sum. Recall that the area of a trapezoid is found by
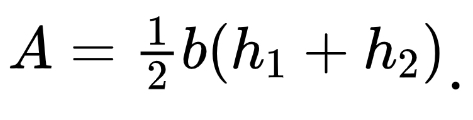
In essence, we are multiplying the base by the average of the two heights. Using the original example function, that gives an estimate of

Note that in the examples above, each rectangle has the same base of length 1. In many problems, the bases will be of different lengths. Don’t forget to change the bases for each rectangle or trapezoid!
Finally, for some types of functions, it is possible to determine whether a particular kind of Riemann Sum will lead to an overestimate or an underestimate of the integral. For increasing functions, a Right Riemann Sum will always lead to an overestimate, because the right side of every rectangle will be higher than the actual function for that rectangle. Similarly, for decreasing functions, a Right Riemann Sum will always lead to an underestimate because the left side of every rectangle will be lower than the actual function for that rectangle.
6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
This section will challenge your understanding of function notation, limits, and Riemann Sums, but you’ll gain a very deep understanding of the true meaning of a definite integral if you persevere! In the last section, we looked at using various shapes to estimate the area under the curve. As the number of sub-intervals increased, we got a better estimate of that area. If we increase the number of subintervals to infinity (which is impossible, of course), we could get an exact estimate. This is where limits come into play!
At the basic level, we’ve been finding Riemann sums by multiplying the base by the height (defined in various ways). If we increase the number of subintervals to infinity, we can formally link the definite integral with the concept of limits as follows:

That’s a lot to digest! Let’s break it down. As n goes to infinity, it allows us to create infinite subintervals, which, in turn, makes the change in x (our base) arbitrarily close to zero. F at x sub i finds the height of the rectangle at each of the subintervals. The greek symbol Sigma (Σ) tells us we are adding up each of these infinite areas to get the exact value of the definite interval.
To write a definite integral as the infinite limit of a Riemann Sum, we actually need to start by finding Δx and x sub i (the portion that comes after ‘where’ in the formal definition). This will be easier to see through an example.
Let’s say we are asked to write the following definite integral as a limit of the Riemann Sum:
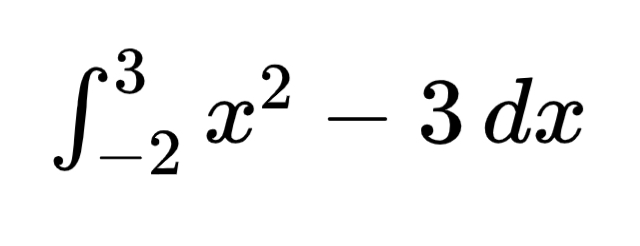
First, we need to find
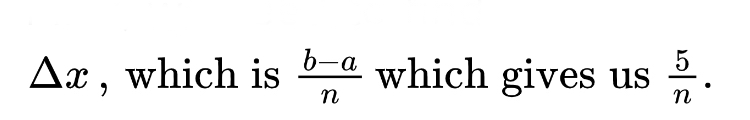
Then, we need to find
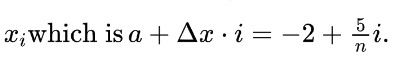
Now, we need to use our knowledge of function notation and substitution to complete the conversion from a definite integral to a limit of a Riemann Sum.
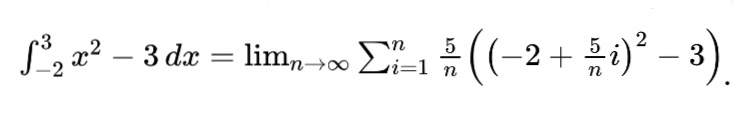
Finally, you may also be asked to work backward from a limit representation of a Riemann Sum to a definite integral. Identifying a, delta x, and f(x) are your main tasks. Let’s look at an example to wrap up this challenging section.
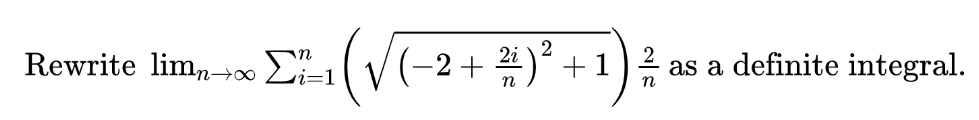
First, try to find delta x by looking for the fraction with n as the denominator. In this case, delta x is 2n. This tells us that the distance between a and b is 2/n. Next, look for that same fraction to be multiplied by i and added to some number. That number tells us the value of a. In this case, we can see that a must be -2. Since the distance between a and b is 2, b must be zero. Almost there!
The last step is to replace the
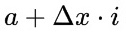
with x so that we can write the function of our definite integral. This gives us an f(x) of
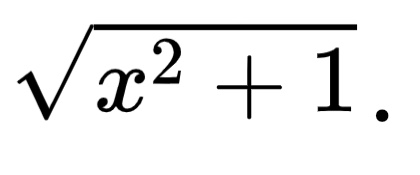
Now we can write the definite integral
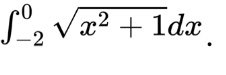
These problems take a lot of practice, but once you commit the process of finding Δx and x sub i to memory, they become very doable. Good luck!
6.4 The Fundamental Theorem of Calculus and Accumulation Functions
Now that we’ve covered some ways of thinking about the accumulation function, which is the definite integral, we’re finally ready to link this concept back to our previous study of derivatives. At the most basic level, you can think of integrals and derivatives as inverse operations. In other words, they “undo” each other. Stated formally, we have:
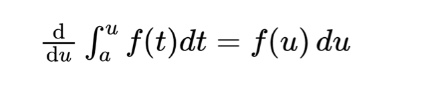
Notice that the derivative of an integral with a function for an upper bound is just the integrand—with the function substituted for the input variable and then multiplied by the derivative of the functional bound. It sounds like a lot, but a few examples will help you see how easy this is!
Best case scenario, the upper bound function is just x as in the example below:
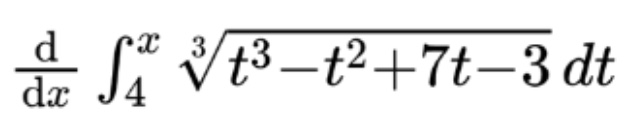
In this case, we substitute the functional bound, x, into the integrand and then multiply by the derivative of x, which is just 1. This gives us:
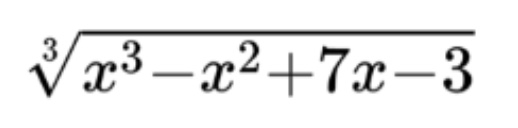
The case is only slightly more complicated when the functional bound is something other than just x. For example,
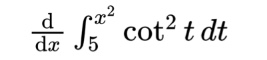
The only difference for this problem is that we will now need to multiply our answer by the derivative of the functional bound, in this case 2x:
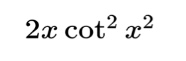
Notice that for all of these problems, the numerical bound has no impact on the answer. In the event that the functional bound is the lower bound, be sure to change the sign of the integral to switch the bounds before proceeding.
On the AP exam, you will be expected to apply this theorem using graphs, equations, and tables of values. Be sure to underline whether the question is asking for a rate of change (derivative) or a total amount (integral).
6.5 Interpreting the Behavior of Accumulation Functions Involving Area
These types of questions typically involve a verbal and graphical description of an integrally-defined function and ask about various aspects of that function’s behavior: increasing/decreasing, concavity, relative extrema, and absolute extrema. You’ll need to pay careful attention to the relationship between any functions provided and the graphs provided because they typically aren’t the same function.
Let’s look at a quick example.
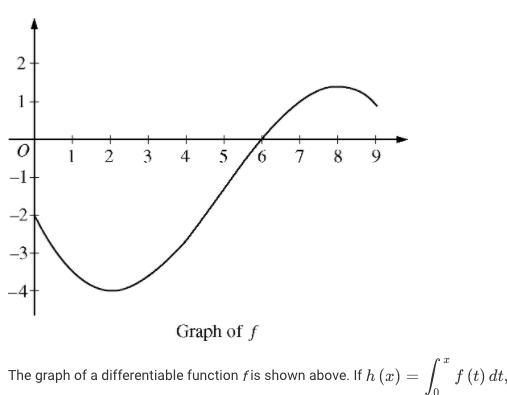
Image Courtesy of Chegg.com
The first thing you should note is the relationship between the integrally-defined function and the graph provided: the graph shows the derivative of the function h. Knowing this helps us answer questions about where h(x) is increasing or decreasing. For a function to be increasing, its derivative must be positive. If we connect this to the graph of the derivative above, we are looking for where the graph is positive, which means above the x-axis. So h(x) is increasing when 6<x<9 because the derivative, f(x), is positive over that interval.
Other times, the prompt asks about the concavity of h(x). Concavity is a function of the second derivative and we have a graph of the first derivative. This means that to examine the concavity of h(x), we need to be looking at the slope of the graph of f(x). Let’s say the prompt asks where h(x) is concave up. Since we have the graph of the derivative of h(x), we need to find where the slope of f(x) is positive because that would be a positive second derivative of f(x). In other words, h(x) is concave up when 2<x<8.
Using that same line of reasoning helps us find inflection points. Recall that inflection points occur when the second derivative changes sign. If we need to find inflection points for h(x), we need to look for slope changes in the graph of f(x). At x=2, we see that f(x) has a slope change from negative to positive, so x=2 is an inflection point of h(x). Similarly, at x=8, we see that f(x) has a slope change from positive to negative, so x=8 is also an inflection point of h(x).
Finally, if the prompt is asking about a relative or absolute extrema, we need to focus on the definition of these concepts. Relative extrema occur where a function changes from increasing to decreasing (a relative maximum) or decreasing to increasing (a relative minimum).
How about an example? If we need to find all the relative extrema for h(x), we use the derivative graph, f(x), to find changes in sign of the first derivative. In terms of the graph, this is where the graph of f(x) crosses the x-axis. At x=6 we have the only relative extreme. At x=6 the first derivative goes from negative (below the x-axis) to positive (above the x-axis), so x=6 is a relative minimum.
For absolute extrema, you will repeat the same process and identify candidates for the absolute maximum and absolute minimum for the integrally defined function. Then you will use your accumulation function skills to evaluate the value of h(x) at those values of x. You will also have to check the endpoints (in this case x=0 and x=9) as potential absolute extrema. Be sure to pay attention to whether the question asks for where the extreme occurs (an x-value) or what it is (the y-value).
6.6 Applying Properties of Definite Integrals
This type of question asks us to recognize that we can combine a series of known integrals to evaluate an unknown definite integral. If we think about our previous work with adding up geometric shapes over certain intervals of x, this process makes intuitive sense. Let’s look at an example to help clear this up.
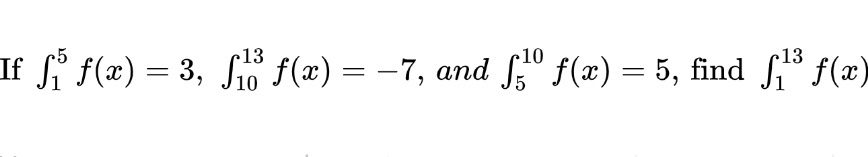
Here we are given three known definite integrals and asked to find an unknown definite integral. That unknown integral covers x-values from 1 to 13. If we add up the integrals that cover this range of x-values, we can find the value of the unknown integral. This leads us to
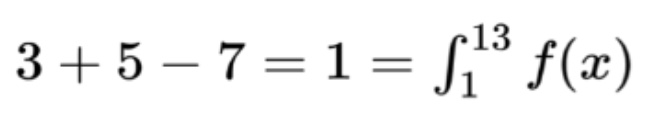
Sometimes, we have to use subtraction to arrive at the integral in question. For example
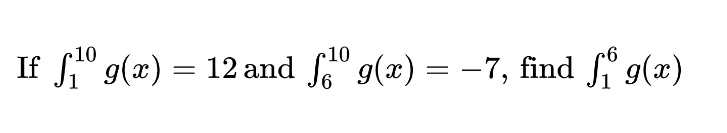
can be solved by subtracting the second known integral from the first known integral. This is because we are essentially removing the x-range that we don’t need from the first integral, which leaves behind the portion that we do need. That means

Finally, in some cases, you will need to negate a given integral in order to reverse the bounds. A quick example should suffice.
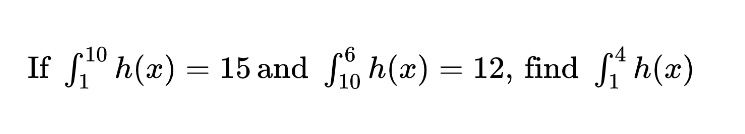
In order to find the requested integral, we need to remove the integral that covers the x-values from 6 to 10 from the larger interval that covers the x-values from 1 to 10. However, we are given a definite integral that covers the x-values from 10 to 6 instead (x-values are decreasing instead of increasing). To fix this, we simply negate the integral to reverse the direction of the bounds.
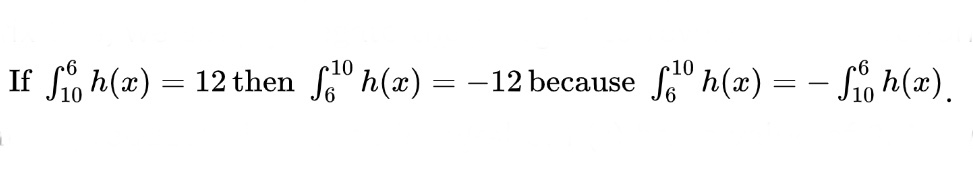
This means that the requested definite integral of h(x) has a value of 3. On to the next section! 💨
6.7 The Fundamental Theorem of Calculus and Definite Integrals
In a previous section, we looked at how integrals and derivatives relate to one another. Now we’ll look at another part of the Fundamental Theorem of Calculus (FTC) that demonstrates the relationship between a definite integral and its antiderivative, the result of an integral.
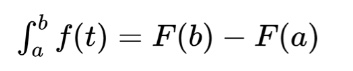
This is read as “the integral from a to b of f(t) equals the antiderivative F at b minus the antiderivative F at a.” We’ll get into the mechanics of how to evaluate definite integrals by hand in a later section. In this section, we’ll explore how to solve these questions when directly integrating a function is impossible or extremely unpleasant.
Sometimes these FTC problems appear in the calculator section and present derivatives that would be a nightmare to integrate by hand. For example,

At first glance, this looks impossible. However, FTC suggests a way to set up the problem as
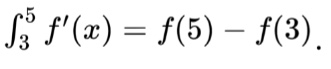
Our calculators can evaluate the definite integral from 3 to 5 of the derivative of f. Once we have that number, it’s an Algebra 1 problem. This gives us
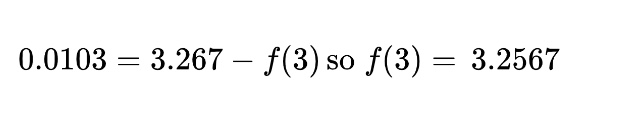
These problems can also use a table of various values of a function, its derivative, and/or its antiderivative. For example, the FTC provides the setup if we are given a table of values for a twice-differentiable function, f(x), and its derivative and asked to find
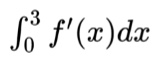
| x | 0 | 1 | 2 | 3 |
| f(x) | -12 | -3 | 4 | 7 |
| f'(x) | 15 | 4 | 7 | -5 |
Using the FTC we get
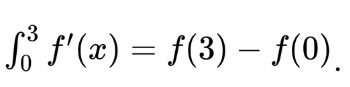
Now we just need to pull the correct values from the table to get our answer. 7 minus -12 gives us a final value of 19!
6.8 Finding Antiderivatives and Indefinite Integrals: Basic Rules and Notation
We are finally ready to start finding antiderivatives by hand 🎉 At this point, you likely understand that an antiderivative is a function, or family of functions, that has/have a given derivative. We are basically reversing the derivative process to find antiderivatives. Let’s talk about what we mean by a family of functions first before we dive into reversing the derivative process.
Let’s say we have two different antiderivatives,
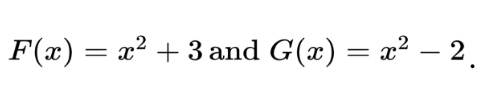
If we were to take the derivative of both of these functions, we would find that they both have the same derivative, 2x. If we reverse the derivative process through integration, how do we account for arriving at these two different antiderivatives? Introducing the magical constant C!
When we integrate 2x, the antiderivative is 2x+C where C is any constant. This result is often referred to as a family of functions because they vary only in the value of their constants and all share the same derivative. This type of integral is referred to as an indefinite integral because we can’t be sure which member of the family of antiderivatives is at play. If the bounds of the integral are not specified as they are in a definite integral, always add ‘+C’ to the end of your antiderivative!
Now let’s look at how to reverse the process of some of the derivatives we learned early in our study of calculus.
Polynomials
To integrate polynomials, we will add one to the exponent of each term and divide by the new exponent. Rewriting with negative exponents is often a useful trick! For example:
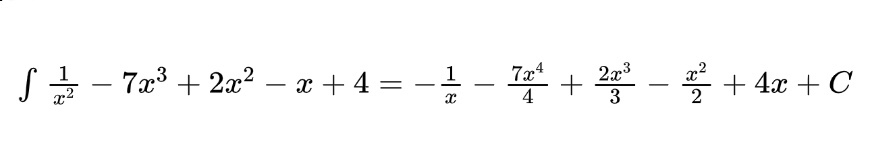
Note that the same logic applies to radical functions since they can be rewritten with fractional exponents.
Trigonometric Functions
When you are first learning your trig antiderivatives, you may find it useful to think to yourself “what has a derivative of . . ?” Here are the basic trig integrals you need to know for the AP exams:
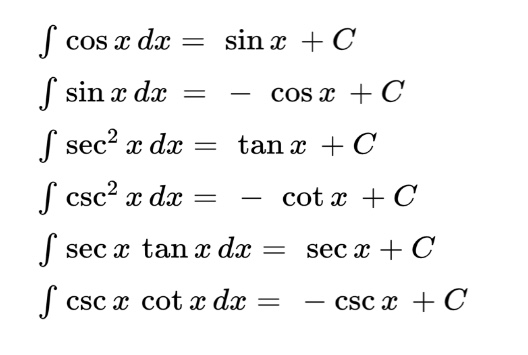
Inverse Trigonometric Functions
These integrals aren’t nearly as common on the AP test, but below are the forms you may encounter on the AP test.

Transcendental Functions
Finally, we have the integrals for the transcendental functions you are likely to encounter on the AP exams:
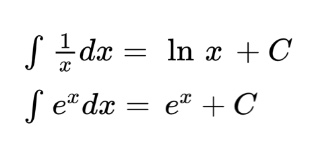
So many integrals to memorize! Here's a tip: use the spaced repetition study technique to create flashcards with all the integrals and review them periodically before the AP exam.
6.9 Integrating Using Substitution
Now that we’ve learned how to integrate when the variable is just x, we need to expand our skills to include functions more complicated than x. U-substitution is used to integrate these more complicated functions. Recognizing these functions is similar to recognizing functions that would require the chain rule when taking a derivative. We are basically reversing 🔄 the chain rule process now!
For example, if we have
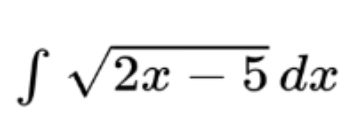
we have a square root of a function that is more complicated than just x so we need u-substitution. To carry out u-substitution, we replace the more complicated function with the substitution, u. This means, u = 2x-5. We also need to replace the derivative of x, dx, with the derivative of u, du, in order to integrate (you probably never thought much about that ‘dx’ in all the previous integral problems, but you need that in order to integrate). In this case, the derivative of u is 2. In this example integral, we don’t have the ingredients for du, but we can make it by using a special version of the number 1!
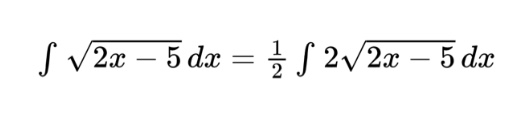
Since we needed a 2 dx to create du, we multiplied the right side of the integral by 2 and balanced this operation by multiplying the left side of the integral by one half. Note that you can only multiply by constants to create du.
This gives us
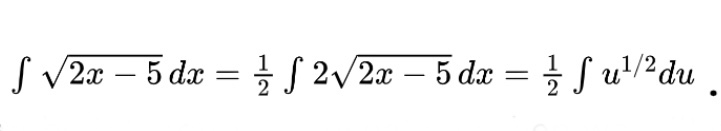
That integral in terms of u can be integrated as usual and then we will convert back to x for the final answer.
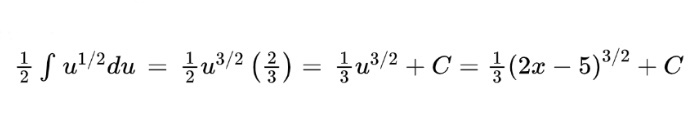
This same process applies when you have complicated trig functions or transcendental functions. Let’s take a look at a quick example before we explore u-substitution for definite integrals.
If we have
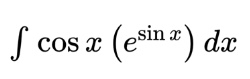
we may be tempted to search for a product rule for integration (there is one, but not until BC calc!). However, this kind of integral is actually a u-substitution problem! If we use u=sin x, du would be cos x. This makes everything much easier.
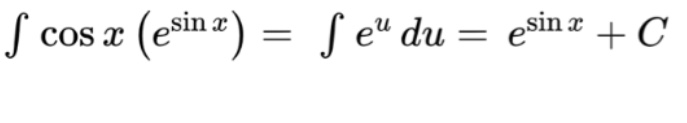
Obviously, choosing the correct u is very important and requires some trial and error. If the integral doesn’t work with your first guess at u, try something else!
Finally, let’s look at how u-substitution works for definite integrals. For example,
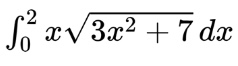
would definitely require u-substitution. When we have a definite integral, we have to remember to change our integral bounds so that they are also in terms of u. If you write an integral that is in terms of both u and x, it is automatically wrong on the AP exam!
To complete this problem, first, we choose u, which should be
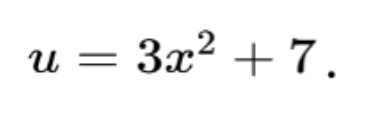
This means that du will be 6x so
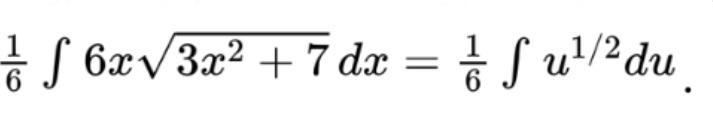
Notice that we didn’t write any bounds so far! We can convert from x to u using the equation we wrote to define u in the first place.
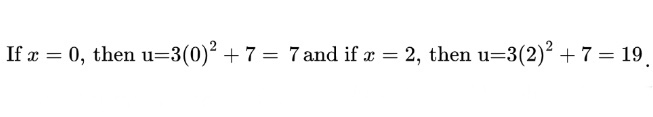
This gives us the final integral in u form
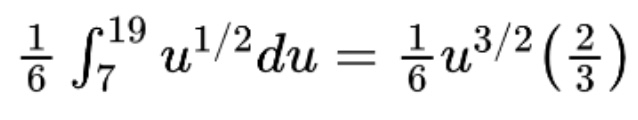
We do NOT have to convert back to x to get our final answer because we can evaluate using the u bounds. Therefore, our final answer is
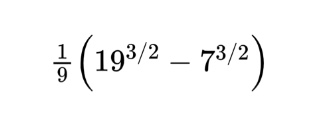
6.10 Integrating Functions Using Long Division
While not common, occasionally you’ll have to use polynomial long division or completing the square in order to integrate. It may have been a while since you have used these skills!
A long division problem can be recognized when the degree of the numerator is higher than the degree of the denominator. If you use long division to write an equivalent form of the problem, more basic forms of integration will work! Just remember to write the remainder as a fraction over the divisor.
For example, if we have the integral on the left below, we can use long-division to rewrite it as the integral on the right and then integrate term by term.
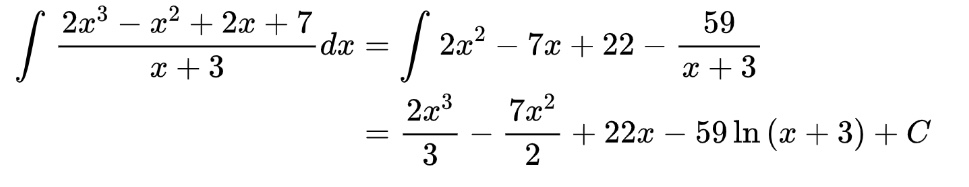
Usually, these problems appear in the multiple-choice section and a quick look at the answer options can tell you that you may be looking at a long-division integral. If you see multiple answer options that start off as polynomials and end with a natural log term, that is a strong indicator of a long-division integral. For the last several years, this type of problem has appeared, at most, as one problem in the multiple-choice section. Let’s look at the other type of rare integrals on the AB test.
Identifying a completing the square problem is a bit more challenging. In general, if all of your other techniques fail, try completing the square. The majority of these problems appear in the multiple-choice section. If you are having difficulty with an integration problem and nothing appears to work, take a look at the answer options. If you see multiple answer options with complicated inverse trigonometry answers, you may be looking at completing the square integral. Let’s take a look at an example…
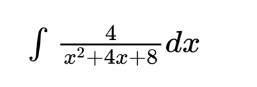
As with all integrals, you should try your basic methods before attempting any of the more complicated forms of integration. Clearly, this isn’t a standard form integral, so one would first attempt u-substitution. If we set the denominator as u, we run into a problem: there is no x in the numerator with which to create a du. It is also not in the correct format to create any of our inverse trig integrals. Finally, it does not meet the criteria for long division. Once you have eliminated ALL other possibilities, you should attempt completing the square (full disclosure: these efforts are typically guided by the multiple-choice answers provided).
To start the process of completing the square, we look at the denominator and determine the constant necessary to complete the existing quadratic. In this case, we need a 4 to complete the square. This can be accomplished by some creative rewriting of the existing denominator as shown below…
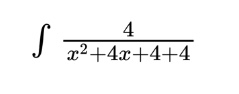
Next, we need to write our trinomial as the sum of squares we have created. This process is shown below.
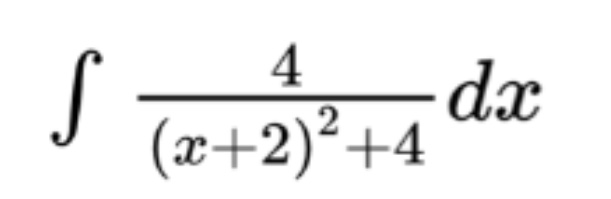
The next step is not necessarily intuitive. You should be starting to sense that we are heading towards an inverse trig solution. As such, making the numerator a one would make the integral easier. To factor out a 4 for the entire integral, we need to do a bit more creative rewriting. Specifically, we need to rewrite the square term in the denominator…

As you can see, we have rewritten the square term with a convenient form of one as the coefficient (4/4). This allows us to cancel out a four from the entire integral as shown below…

Now, hopefully, you recognize that this is an inverse tangent problem that also requires u-substitution. In the next step, we choose the expression for u.
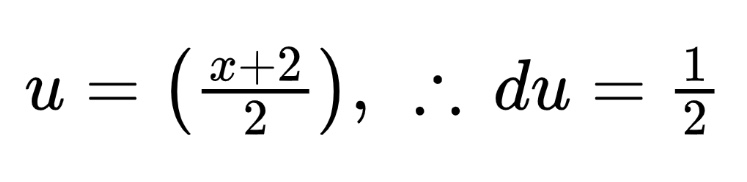
The three dots are mathematical notation for "therefore." Using this substitution, we arrive at the following u integral.
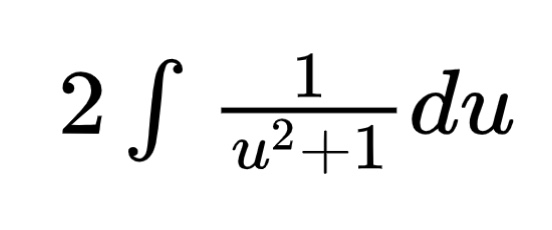
Now, we can see the standard form of the inverse tangent integral. This gives the following antiderivative in terms of u.
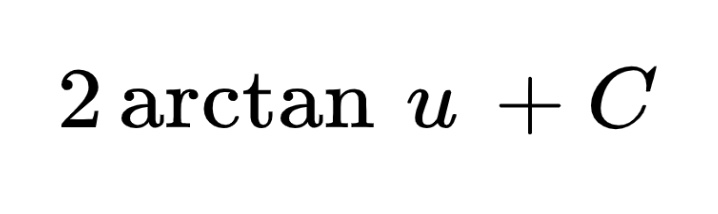
We are almost finished! The last step is to rewrite the antiderivative in terms of u.
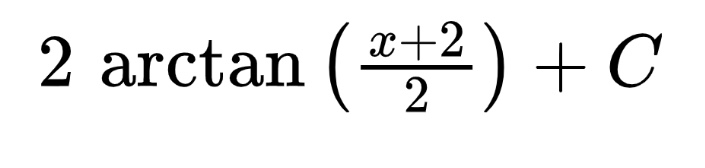
It was quite the journey, but we made it! Generally speaking, this is the hardest integral form on the AB test. It requires a student to have full mastery of algebra, u-substitution, and inverse trig integrals. However, if past tests are representative of future tests, this content appears, at most, as one question on the multiple-choice. If you don’t fully grasp this concept, fret not! If you focus on mastering the other forms of integration, a 5 is well within reach!
6.11 Integrating by Integration by Parts (BC ONLY)
Have you ever noticed that there hasn’t been a product rule counterpart for integration yet? That’s where integration by parts comes in handy! If you encounter an integral that looks like a product and you have ruled out u-substitution, you are likely looking at an integration by parts problem. When we encounter the integral of a product, we assign one of the factors to be u and the other to be dv. Then we apply the following formula:
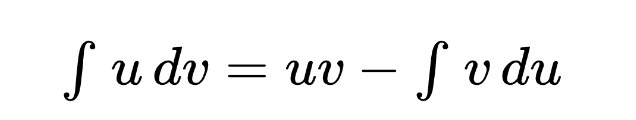
Choosing which factor will be u and which will be dv is an art form that requires practice. Generally speaking, you want to choose a dv that is easily integrated and choose a u that makes the integral on the right side of the equation easier than the integral that you started with!
Let’s take a look at an example. If we encounter

we should recognize that this is the integral of a product and thus requires integration by parts. If we choose the exponential as u and x as dv, we’ll end up with a more complicated integral than we started with, so this is unwise. If we try the other option, we are much more successful.
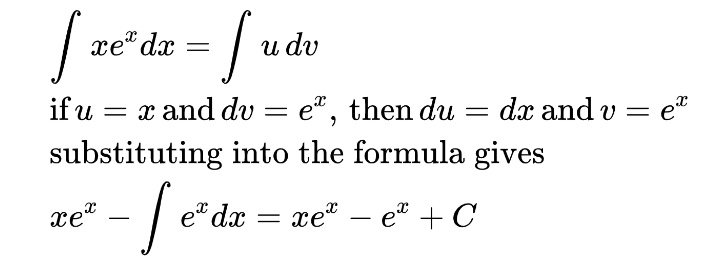
This process takes practice! Remember, if you get a more complicated integral than you started with, switch your choices for u and dv. Also, in some cases, you will have to repeat the integration by parts process more than once because the new integral is also a product. This typically happens with trig functions. Keep going and you should arrive at an answer.
6.12 Integrating Using Linear Partial Fractions (BC ONLY)
Some integrals of rational functions cannot be integrated using u-substitution, inverse trigonometry, or other techniques we’ve explored so far. When we see the integral of a rational function where the degree of the denominator is higher than the degree of the numerator AND it appears the denominator can be factored, we can use integration by partial fractions.
To carry out this technique, we need to use partial fraction decomposition. In essence, partial fraction decomposition is the process of undoing a common denominator so that a rational function can be re-written as the sum of rational functions with linear denominators. You’ll need to solve a basic system of equations to carry out this technique.

Remember to check your factoring before you proceed with the decomposition. Those minor errors lead to wrong answers that are always one of the available answer choices in multiple-choice.
6.13 Evaluating Improper Integrals (BC ONLY)
Improper integrals refer to integrals that either a) have infinite limits of integration (one or both limits are infinite) or b) are not defined at some number in the interval of integration. We use the limits below to assess the first type of improper integrals:
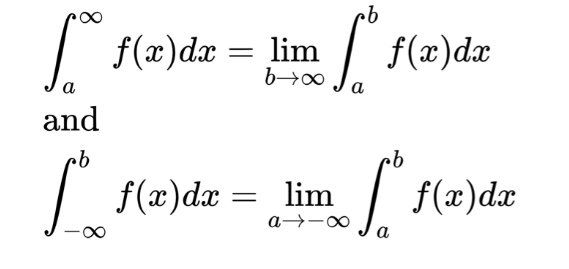
If these limits exist and are real numbers, the improper integral is said to converge. If the limit does not exist or is infinite, the improper integral diverges. If both limits of integration are infinite we use
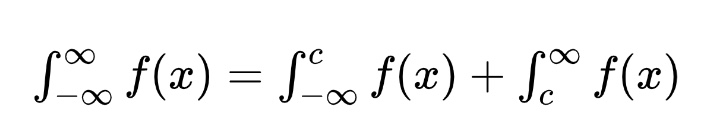
The choice of c is arbitrary, but zero is usually an easy choice. If either of the integrals in the sum diverge, then the improper integral diverges.
Some examples will be useful:
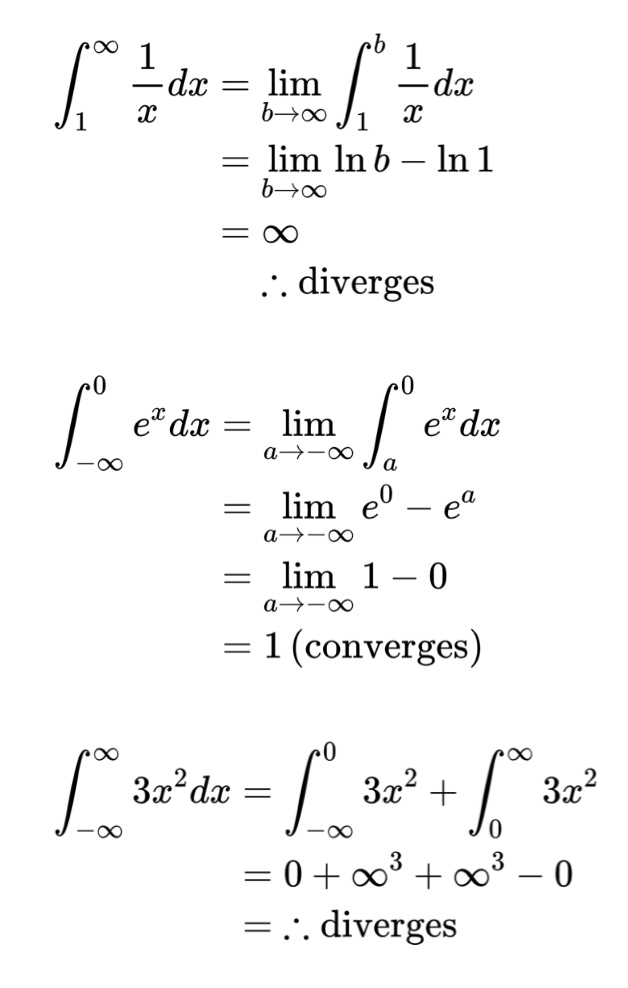
For the final type of improper integral, if the function is not defined at some point in the interval of integration, we use the following:
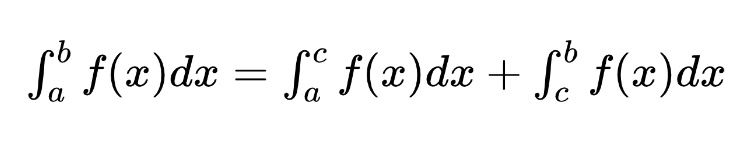
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
6.0Integrating Using Substitution
- Introduction
- 6.1: Exploring Accumulations of Change
- 6.2 Approximating Areas with Riemann Sums
- 6.3 Riemann Sums, Summation Notation, and Definite Integral Notation
- 6.4 The Fundamental Theorem of Calculus and Accumulation Functions
- 6.5 Interpreting the Behavior of Accumulation Functions Involving Area
- 6.6 Applying Properties of Definite Integrals
- 6.7 The Fundamental Theorem of Calculus and Definite Integrals
- 6.8 Finding Antiderivatives and Indefinite Integrals: Basic Rules and Notation
- 6.9 Integrating Using Substitution
- 6.10 Integrating Functions Using Long Division
- 6.11 Integrating by Integration by Parts (BC ONLY)
- 6.12 Integrating Using Linear Partial Fractions (BC ONLY)
- 6.13 Evaluating Improper Integrals (BC ONLY)
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.