7.7 Finding Particular Solutions Using Initial Conditions and Separation of Variables
4 min read•june 18, 2024
AP Calculus AB/BC ♾️
279 resourcesSee Units
🎥 Watch: AP Calculus AB/BC - Separable Differential Equations
Continued from 7.6 Finding General Solutions Using Separation of Variables.
General vs. Particular Solutions
A general solution to a differential equation is a family of functions that satisfies the equation. It is possible that there are infinitely many functions in the family that could describe the behavior of the system modeled by the equation. ⭐
However, it is only possible to obtain a unique solution that passes through a specific point. This unique solution is known as a particular solution and can be obtained by using additional information, such as initial conditions.
In other words, a general solution is a description of the behavior of the system in general, without specifying the specific values of the variables at a given time or location. On the other hand, a particular solution takes into account the specific conditions that are present at a specific time or location, giving a unique solution for the system.
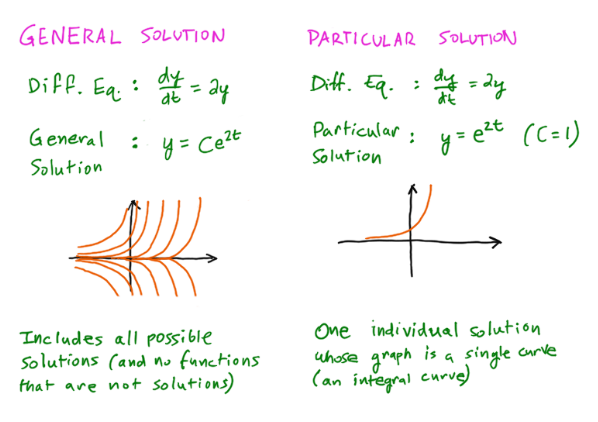
Source: Higher Math Help
Consideration: Domain Restrictions
Solutions to differential equations may not always be defined for all values of the independent variable. There may be restrictions on the domain, or range of values, for which the solution is valid. These restrictions can arise for several reasons, including: 🔸
- Singularities: Certain values of the independent variable may result in division by zero or other mathematical singularities in the solution, leading to an undefined solution.
- Physical constraints: The solution may only be physically meaningful within certain ranges of the independent variable. For example, the position of a projectile may only be defined when it is above the ground, and not when it is below.
- Mathematical constraints: Certain mathematical conditions may be required for the solution to be well-defined. For example, the solution may only be valid for positive values of the independent variable.
It's important to keep these domain restrictions when solving differential equations and interpreting the results. Ignoring the domain restrictions can lead to incorrect or meaningless solutions. To avoid this, it may be necessary to split the domain into several intervals, each with its own solution, or to use different methods to obtain a solution for different parts of the domain.
Example
Let’s look at the differential equation given in Eq. 12:
.png?alt=media&token=011b3f1e-f3e0-42dd-a3ec-2aa2c00eb52a)
If we treat the derivative as a fraction, we can do something that would disgust professional mathematicians*:
.png?alt=media&token=5e424b6b-5e8e-4c01-8cb7-8a23391b999c)
We can perform step 5 because the two sides of the equation are equivalent, thus we can perform the same operation (ie. integration) on both sides and not lose any information.
Continuing the integration:
.png?alt=media&token=1c2e412f-0fa2-4d0f-8197-655ec8e9b67e)
Note that we need two constants because we found two different antiderivatives. However, we can combine them into a single constant:
.png?alt=media&token=66d73364-d781-4527-b7a6-11e7a49bb180)
This statement means that, because the set of real numbers is an infinite set** and both of the constants are real numbers, the difference between them is also a real number, ie. another constant we can call C.
So,
.png?alt=media&token=1450eba6-e9e1-46fe-b5c0-d0bf586e06ce)
Notice that this equation is also equivalent to the solution given in Eq. 12. The solution given in Eq. 27 is a generalization of the solution given in Eq. 12.
Now, let’s say that we have some prior information about the function called an initial condition, eg. y(0) = 1. We can use this information to solve for C:
.png?alt=media&token=e109d196-652a-426a-a850-34d1622bddd8)
This implies that C = 0, which means we have found the specific solution to the differential equation in Eq. 12 along with the condition that y(0) = 1.
We can also revisit the differential equation in Eq. 11:
.png?alt=media&token=fd801cf9-1682-4bed-8c23-f17687f8884e)
We need to take special precautions regarding the absolute value signs when solving for y:
.png?alt=media&token=6c71e3e7-a2bb-4280-8dd9-9669c234ba0a)
So, the general solution is y = C2e^x - 5. For an additional exercise, find a specific solution to the differential equation such that y(ln5) = -6.
Another differential equation that is solvable via separation of variables is the equation below:
.png?alt=media&token=f78536b2-4ebb-4434-9f38-72b2bf27776b)
Notice that if C = 0, the solution to the differential equation is just y = x. If you plug y = x into the differential equation in Eq. 33, you will notice that this returns a valid equality.
Review
Solve the differential equation below given an initial condition and a range restriction. (Hint: rewrite the arcsine expression using the identity that defines a cosine graph as a shifted sine graph and do something similar for the arccosine expression.)
.png?alt=media&token=b5ff0183-64fd-4415-bf60-11c6a12456d0)
Answer
The arc trig expressions are red herrings:
.png?alt=media&token=be7a0a11-5a29-4812-b5ac-741cac992a27)
.png?alt=media&token=b8aa7977-2ff7-4001-a286-dbd7b7282c75)
Footnotes
*This mathematical move is actually incorrect because multiplying the dx term over in that fashion implies that dx is a number and therefore dy/dx is a fraction, which is not true. However, this move is completely acceptable for the AP exam.
**“Infinite” in this context is not well-defined. The actual size of the set is called its cardinality, which is not simply infinity as implied in the statement:
.png?alt=media&token=8c4bd717-0f3a-4b34-a272-ca240d612405)
Some definitions also include zero in the set of natural numbers (the lastly defined set in the statement).
Browse Study Guides By Unit
👑Unit 1 – Limits & Continuity
🤓Unit 2 – Fundamentals of Differentiation
🤙🏽Unit 3 – Composite, Implicit, & Inverse Functions
👀Unit 4 – Contextual Applications of Differentiation
✨Unit 5 – Analytical Applications of Differentiation
🔥Unit 6 – Integration & Accumulation of Change
💎Unit 7 – Differential Equations
🐶Unit 8 – Applications of Integration
🦖Unit 9 – Parametric Equations, Polar Coordinates, & Vector-Valued Functions (BC Only)
♾Unit 10 – Infinite Sequences & Series (BC Only)
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.