Jillian Holbrook
AP Chemistry 🧪
269 resourcesSee Units
A Dive Into Spectrophotometry 🌈
In chemistry, many times we want to calculate how light reacts to a certain colored solution with solute in it. Well, spectrophotometry can do just that!
Spectrophotometry is a technique used to measure the amount of a specific substance in a sample based on its absorption of light. It involves the use of a spectrophotometer, which is an instrument that measures the amount of light absorbed by a sample at a specific wavelength or range of wavelengths.
How Does a Spectrophotometer Work?
To get a better understanding of what spectrophotometry, let's take a look at a spectrophotometer itself:
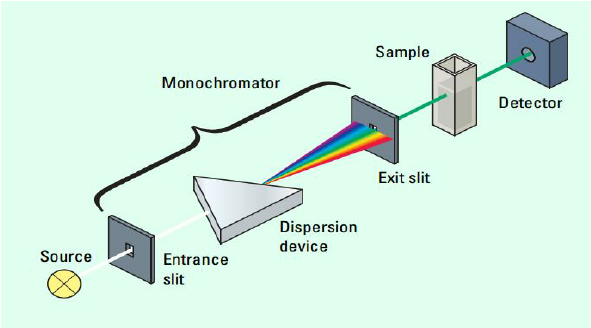
Image Courtesy of ResearchGate
There are three main parts to this machine: the monochromator, the sample, and the detector.
The Monochromator
The monochromator has three main parts: the entrance slit, the dispersion device, and the exit slit. The entrance and exit slips are simple. They are where a beam of light enters and exits the monochromator. However, the dispersion device is the most important part of the monochromator. Essentially, the dispersion device takes a beam of white light and splits it into the full spectrum of colors. The exit slit is placed based on what wavelength of light the experimenter needs for the solution at hand, typically the opposite color (red solution --> green light, etc.)
The Sample
The sample is just that—the sample! It can be any color or type of solution you wish, from a solution of Copper (II) Sulfate to red Gatorade, which we will take a closer look at in a minute.
In a spectrophotometry experiment, samples are poured into cuvettes, which are a type of small transparent tube that allows light to pass through it. The cuvette is then placed in the spectrophotometer, which uses a light source from the monochromator to shine a specific wavelength of light through the sample.
The Detector
The amount of light absorbed by the sample is then measured by the spectrophotometer. Some of the light is absorbed by the solution, while the rest is transmitted through the cuvette. The spectrophotometer measures the amount of light that is transmitted through the cuvette, and this measurement is used to calculate the concentration of the substance in the solution.

Image Courtesy of Research Gate
On the right is the Incident Light (I0) run by the monochromator through the cuvette, and on the left is the transmitted light (I) that is not absorbed by the sample and will be measured by the spectrophotometer.
Color and Absorption
Importantly, the color of an object is determined by the wavelengths of light that it absorbs and reflects. When light hits an object, some of the wavelengths of light are absorbed by the object, and others are reflected. The absorbed wavelengths of light determine the color that an object appears to the human eye. 🌈
For example, if an object absorbs all wavelengths of light except for red, it will appear red to the human eye because the only wavelengths of light being reflected are red. On the other hand, if an object absorbs all wavelengths of light except for blue, it will appear blue.
The absorption of light also plays a role in the intensity of the color. If an object absorbs a lot of light, it will appear very intense and saturated. If it absorbs less light, it will appear less intense and more muted.
This explains why we want to use the light of a wavelength opposite to the visible color of samples, as this type of light wavelength is most readily absorbed by the solution. For example, if we were to run a green light through a green solution, the absorption would be very low or zero because the solution is reflecting green wavelengths of light and allowing the incidental light to be similar or the same as the transmitted light. In other words, we would not get an absorption value that helps determine solution concentration.
Colors that are opposite to one another are known as complementary colors. We can look at the main colors and their complements using a color wheel with light wavelengths:
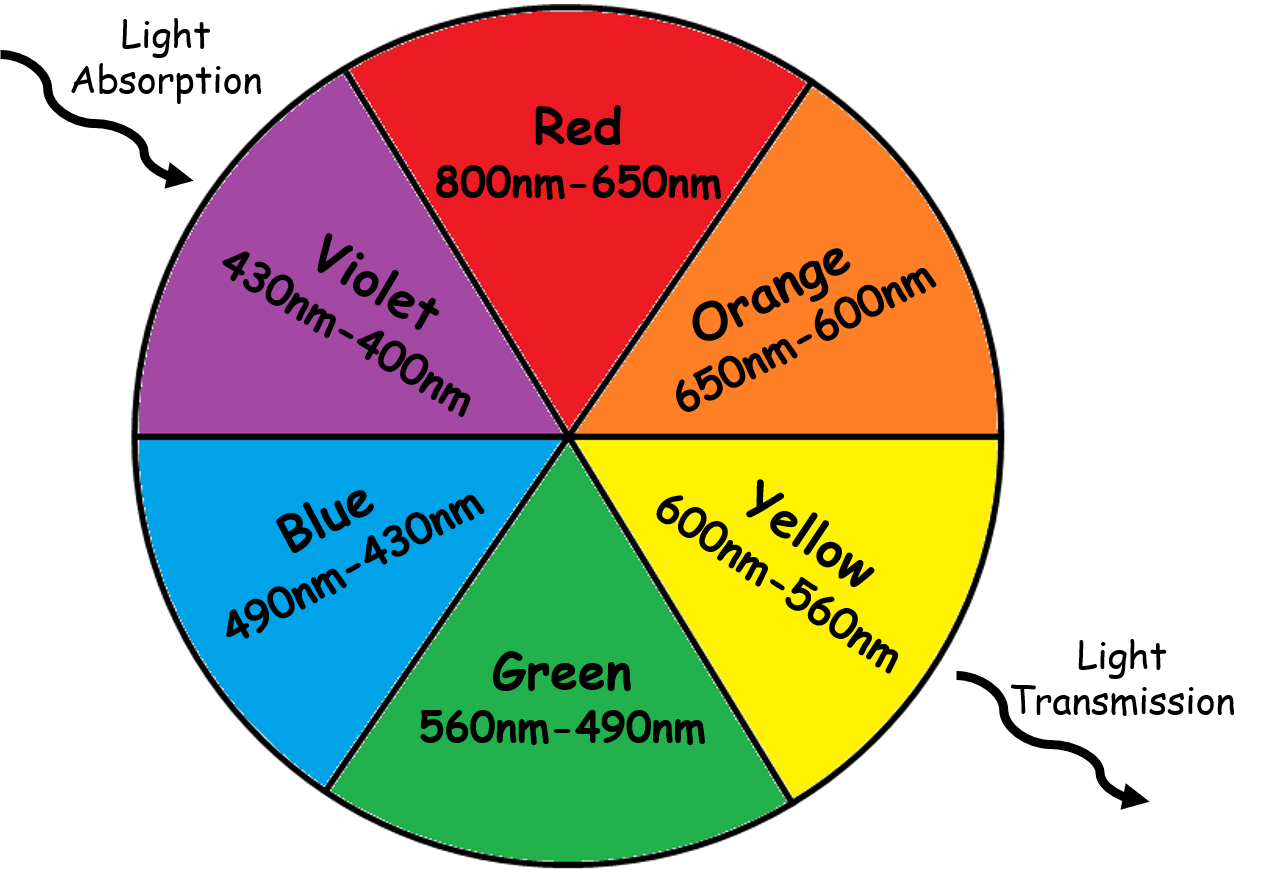
Image Courtesy of Chemistry LibreTexts
Applying the Spectrophotometer: Red Gatorade 🔴
Let's say a chemist is interested in calculating the molar concentration of red food dye in Gatorade. Well, this is a perfect time to talk about spectrophotometry in action!
A chemist would fill a small cuvette, the clear and square form of test tube used by the spectrophotometer, with red Gatorade. Then, they would run it through a spectrophotometer with green light, the complement for a red solution, at around 560–520 nm. The spectrophotometer would measure the transmitted light and provide results for absorption, but how would he find the concentration? Well, luckily scientists have a formula for that! It is known as the Beer-Lambert Law.
The Beer-Lambert Law
The formula for the Beer-Lambert Law is actually quite simple. The Beer-Lambert Law (also known as Beer's Law for short) is a linear relationship between the absorption of light and the concentration of the absorbing species:
A = εbc
where:
A is the absorbance of the solution (this value is unitless)
ε is the molar absorptivity of the substance in L/[(mol)(cm)]
b is the path length of the cuvette in cm (the distance that the light travels through the solution)
c is the concentration of the substance in the solution in mol/L
Once all written out, having several variables may feel a little confusing, but the two variables ε and b are most often constant. The molar absorptivity, ε, of a solute is a measurement of how strongly a chemical species reduces light (reduce here meaning absorbs, NOT takes electrons like in most other contexts) at a given wavelength. Path length, b, is simply the length of the rectangular test tube (cuvette) used by a chemist in the spectrophotometer.
The Beer-Lambert law is a linear relationship, which means that the absorbance of the solution is directly proportional to the concentration of the substance in the solution. This means that if the concentration of the substance in the solution doubles, the absorbance will also double. In fact, we often measure absorption on a linear scale by assuming ε and b to be constant (as mentioned above), leading to the equation A = mc, where m = εb:
Gatorade Example Continued 🔴
Back to our chemist friend. Let's say that they looked up the molar absorptivity, ε, of their food dye, Red-40, and found it to be 2.13 * 10^4 L/(mol)(cm). They run their solution through the spectrophotometer and find an absorption of 0.500. Assuming a path length, b, of 1.0 cm, we can use Beer's Law to calculate the molarity!
A = εbc
0.5 = (2.13 * 10^4 L/(mol)(cm))(1.0 cm)(c)
c = 0.5/2.13 * 10^4 = 2.3 * 10^-5 mol/L
And boom! Using the Beer-Lambert Law, we were able to find the concentration of Red-40 in Gatorade with an absorption of 0.5 to be 2.3 * 10^-5 mol/L.
🎥 Watch: AP Chemistry - The Beer-Lambert Law
To enact the type of lab experiment that you would do for this key topic, you can use PhET simulations:
👉 Engage: AP Chemistry - Beer's Law Lab
Practice AP Question for this Unit 🤓
In one of our previous guides, we went over part a from question #5 on the 2019 AP Chemistry Exam. Now, let's go over part b using what we have learned about light and wavelengths.
To look over the in-depth explanation of part a, head back to guide 1.6!
Part b is asking us for the wavelength of something. First off, there are two equations that involve the wavelength of light:
- E= hv, where Planck's Constant h = 6.626 x 10^-34 (m^2)(kg)/s
- c = λv, where the speed of light c = 2.998 x 10^8 m/s
That something we are looking for is the energy needed to remove an electron from the valence shell, or the ionization energy/binding energy. ⚡ So let's solve for the wavelength of this energy!
The only piece of information they give us is the actual energy itself, but there are six different types of energy listed on the chart. What do we do? 😕
To recall, the binding energy is the highest where the nucleus is located. Thinking about valence electrons, we should be using the lowest binding energy. Referring to the lowest energy on the chart, we now know that E = 0.980 x 10^-18 J. With this information, we can solve for frequency!
E = hv --> 0.980 x 10^-18 = (6.626 x 10^-34) (v)
v = 1.48 x 10^15
Now that we have frequency, we can solve for wavelength using c = λv.
2.998 x 10^8 = (λ) (1.48 x 10^15)
For our final answer, we get that: λ = 2.03 x 10^-7 m
Great work. This is an example of using both equations for wavelength to solve an FRQ! 🧠
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
🧐Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.