7.11 Introduction to Solubility Equilibria
3 min read•june 18, 2024
Dylan Black
Jillian Holbrook
AP Chemistry 🧪
269 resourcesSee Units
What Is Solubility Equilibria?
In AP Chemistry, we spend a good deal of time discussing solubility, that is, whether or not a solute can dissolve in a solvent, the latter almost always being water. However, after discussing equilibrium, we can apply these ideas to the dissolution of various compounds that we previously classified as insoluble.
In reality, everything dissolves to some extent; we are just describing to what extent dissolution occurs. For example, NaCl is able to dissolve much easier than a substance like PbI2, which we would usually call insoluble. However, we can still write out the reaction for the dissolution of PbI2:
PbI2(s) ⇌ Pb2+(aq) + 2I-(aq)
You may think that this reaction simply does not occur because we call PbI2 “insoluble,” but instead, this reaction just has a tiny K value. In fact, for the dissolution of lead iodide, the K value is 4.41 x 10^−9. When dealing with the equilibrium of dissolution, we call this value Ksp, where sp is short for solubility product. We call it the solubility product because when finding Ksp, we simply have to multiply [Pb2+][I-]^2 (or generally the product of the reactants raised to their stoichiometric coefficients) because we do not include solids in equilibrium calculations.
For extremely soluble compounds such as NaCl or KOH, our Ksp will be well above 1, further reflecting that its dissolution goes far forward. When dealing with Ksps of this magnitude, we often think of the reaction as going in one direction because, in many cases, most, if not all, of the solute dissolves. However, we cannot think that when Ksp is very small, such as in the case of lead iodide.
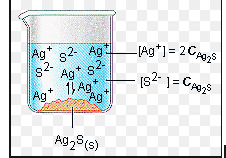
Calculating Ksp
When dealing with solubility, we often see two major measures of how soluble a compound is. The first is grams per liter, and the other is moles per liter or molarity. When doing calculations involving calculating Ksp or finding solubility, you want to be sure to convert from grams per liter to molarity.
Let’s look at a sample problem involving converting and calculating our solubility product:
The solubility of PbCrO4 is 4.5 * 10^-5 g/L. What is its solubility product?
Let’s start by writing out the expression for the dissolution of lead chromate:
PbCrO4(s) ⇌ Pb2+(aq) + CrO42-(aq)
Next, let’s convert from g/L to mol/L:
4.5 * 10^-5 g/L * 1mol/323.2g = 1.4 * 10^-7 mol/L.
Finally, we can plug into our formula for solubility product:
Ksp = [1.4 * 10^-7][1.4 * 10^-7] = 1.9 * 10^-14.
Remember that if you have coefficients, you also need to adjust your equilibrium concentrations before solving for Ksp!
Calculating Molar Solubility
Calculating molar solubility is essentially the same as solving for equilibrium concentrations as we did in Unit 7.7. However, we need to again keep in mind that our solid reactant is not included in concentrations or equilibrium calculations. However, we can return to our best friend, the (R)ICE Table!! Let’s apply these new concepts to a practice problem:
Calculate the molar solubility of CaCO3 (Ksp = 3.36 x 10-9).
The equation for the molar solubility of CaCO3 is as follows:
CaCO3 (s) ⇌ Ca2+ (aq) + CO32- (aq)
Let’s fill out an ICE Box and solve for concentrations!
Reaction | CaCO3 | Ca2+ | CO32- |
Initial | ---- | 0.00M | 0.00M |
Change | ---- | +x | +x |
Equilibrium | ---- | x | x |
Finally, plugging into Ksp and solving, we find: x^2 = 3.36 x 10^(-9) ⇒ x = 5.8*10^(-5).
Relating Qsp and Ksp
Like regular equilibrium, we can also relate Ksp to the reaction quotient to see if a precipitation reaction will produce more or less precipitate to adjust to equilibrium. Like before, if Q > K, the reaction will produce more reactant. If Q < K, the reaction will produce more product. And if Q = K, the reaction is at equilibrium.
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
🧐Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.