7.10 Reaction Quotient and Le Châtelier’s Principle
5 min read•june 18, 2024
Dalia Savy
Dylan Black
AP Chemistry 🧪
269 resourcesSee Units
In the last section, we discussed the concept of Le Châtelier’s Principle and described how it can be used to predict changes in concentrations as a result of external stress being placed upon a system. However, why does Le Châtelier’s Principle actually work? We learned some rules last time and sort of “logic'd” 💪 it out, but in this guide, we’ll take a look at how Le Châtelier’s Principle is justified by using Q, the reaction quotient.
Review of the Reaction Quotient, Q
Earlier in this unit, we discussed the value Q, a number called the reaction quotient. We examined how this value could tell us how an equilibrium would shift based on conditions not at equilibrium. For example, if we found that Q was less than the assigned K value for a reaction, our reaction would respond by increasing the concentration of products in order for Q to become K. Remember that when Q = K, our system is at equilibrium and thus there will be no more changes in concentrations all else held equal. A reaction will basically proceed to make Q equal to K.
The formulas for Q and K look exactly the same, but remember that with Q we can calculate the value at any concentration, whereas at K it is only equilibrium concentrations. This way of thinking about Q vs. K will help guide our mathematical justification of Le Châtelier’s Principle for concentration and pressure, but we’ll also see how temperature stands out as an exception to using Q to justify.
Applying Q To Le Châtelier’s Principle
Concentration
As we learned in the last section, increasing the concentration of products or reactants will cause the system to respond by creating more of the other side. For example in reaction A ⇌ B if the concentration of B was increased, the system would respond by increasing the production of A and vice versa. Let’s think about how Q might help us understand why this occurs.
We know that Q is the ratio of products over reactants raised to their stoichiometric coefficients, so if we increase a concentration on either side, we’re either increasing Q in the case of adding products or decreasing Q in the case of adding reactants. This will change the value of Q to be greater than or less than equilibrium and thus will cause the reaction to respond by shifting back to equilibrium.
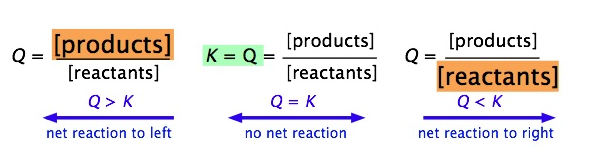
Image Courtesy of LibreTexts
As seen in the above image, when the concentration of products increases from equilibrium, we will find that Q > K and thus there will be a net reaction towards the products and vice versa. Just remember we're always trying to go back to Q equaling K.
Pressure
Similar logic can be applied to pressure, however in this case, we want to give special attention to the exponents on the reactants and products when calculating Q. When learning about Le Châtelier’s Principle, we found that when pressure was increased on a system, we shift towards the side with fewer moles of gas and vice versa. This means that the stoichiometry of the reaction matters with changes in pressure.
To understand how Q relates to pressure let’s look at the value of Q when dealing with partial pressures:
We can define a value Qp similar to the way we define Q by being the ratio of partial pressures raised to their stoichiometric coefficients. Let’s suppose our reaction is A + B ⇌ C.
Qp = P(C)/P(A)*P(B)
The same rules between Q and Kc apply to Qp and Kp. If our overall pressure increases, our partial pressures will also increase proportionally to the overall increase (remember, PA = XA * P where XA is the mole fraction of A). Let’s suppose our pressure increased by a factor of 2. This means that our new Qp will be:
2P(C) / 2P(A) * 2P(B)
However, we can cancel out our 2 in the numerator and one 2 in the denominator to find that at the end, only the denominator will be multiplied by a factor of 2. This means that our reactant pressure has gone up making Qp < Kp, shifting the reaction towards the reactants. The same logic could be applied if our pressure went down by a certain factor.
However, let’s suppose our reaction was instead 3A + B ⇌ 2C. Same as before, we can write out Qp = P(C)² / P(A)³ * P(B) and then imagine that our pressure increased by a factor of 2:

We can then cancel out the 2² to find that our denominator is increased by a factor of 4 and the numerator's increase has been canceled out. This means that Qp has decreased. Therefore, Qp < Kp, and our reaction will proceed by creating more products in response to an increase in pressure. The opposite would occur with a pressure decrease.
This shows us that when the pressure increases or decreases, it is the number of moles of gas on either side of the reaction that has an impact on the direction of equilibrium.
Temperature as the Exception
Unlike concentration and pressure, Q is not used to explain Le Châtelier’s Principle when it comes to changes in temperature.
In the last section, we addressed temperature and Le Châtelier’s Principle by describing heat as either a reactant or a product of a reaction based on whether a reaction is exothermic or endothermic. However, that isn’t quite what actually happens.
While this way of thinking is valid and will get correct answers, what is happening, in reality, is that the equilibrium constant is changing! Although we never discuss K changing, remember that in reality, it’s a temperature-dependent value. This means that K is only constant when the temperature is constant. Based on your reaction, K will either increase or decrease when the temperature is increased. This is when thinking about heat as a reactant or product, and it will help figure out the direction the reaction will go. Just keep in mind that this part of Le Châtelier’s Principle is not justified by using Q.
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
🧐Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.