Dalia Savy
Dylan Black
AP Chemistry 🧪
269 resourcesSee Units
So far in unit 7, we’ve represented equilibrium both in terms of reactions (Ex. A ⇌ B) and mathematically. In this section, we’ll start looking at how we can view equilibrium using particulate models. Particulate models refer to models that represent matter as discrete particles, rather than as a continuous fluid or field.
In the last few sections, we’ve gotten bogged down in math on math on math calculating everything from equilibrium constants to equilibrium concentrations. While knowing the math behind equilibrium is good and definitely applicable to the AP exam, it is just as important to have a firm understanding of what exactly equilibrium is and how we can represent it pictorially. It's time to switch from the technical to the visual real quick!
As you know, equilibrium describes how far forward a reaction goes. Some reactions go forward nearly entirely whereas others do not go forward much at all. This means that at equilibrium, the concentrations of products for various reactions may vary (and we've seen this).
Particulate Diagrams
On a particulate level, this can be described as seeing more product than reactant or more reactant than product at equilibrium. An easy way to remember this fact is also to use the math we’ve learned! For example, take a look at the following practice problem:
Consider the following reaction:
C₂H₄ +X₂ ⇌ C₂H₄X₂
where X₂ can be Cl₂ (green), Br₂ (brown), or I₂ (purple).
Examine the three figures below representing equilibrium concentrations in this reaction at the same temperature for the three different halogens.
Rank the equilibrium constants for these three reactions from largest to smallest.

We could count each product molecule and reactant molecule and divide for each particulate model, however, let’s remember that equilibrium simply tells us how far forward a reaction goes. The higher the equilibrium constant, the more forward a reaction is going. This should make sense since K is the ratio of products over reactants. If K is large, that means there are more products, which is why the reaction is shifting more toward the products.
Therefore, we can simply compare the number of product molecules between the three vessels and find that (a) has the largest K and (c) has the smallest with (b) laying in the middle.
Practice Problem
Consider the following particulate diagram and determine which way the reaction has shifted:
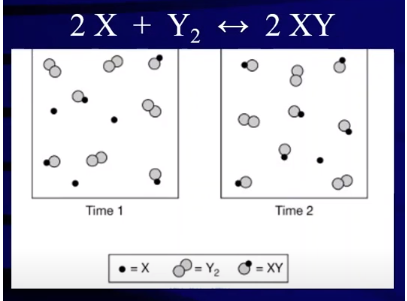
Image Courtesy of Abigail Giordano
Let’s figure out which direction the reaction has shifted by comparing the amount of product (XY) in the vessels at time 1 and time 2. At time 1, we have 4 XYs and at time 2, we have 5 XYs implying that our reaction has produced products over the time period.
Our reaction has shifted right over this time period. We can see that the reaction went further forward because we see an increase in the concentration of products and conversely we see a decrease in the concentration of reactants. At time 1, there are 3 X molecules and 4 Y₂ molecules. At time 2, we see that both of these values have decreased and we now have 1 X molecule and 3 Y₂ molecules. Taking a look at the reaction, we see a reduction in concentration equal to the stoichiometric coefficients in the reaction. This tells us that in fact we saw a conversion of reactants into products, furthering the idea that the reaction shifted to the right.
Now let's think about what the box would look like at time two if the reaction shifted in the opposite direction. In other words, what would happen if, from time one, our reaction shifted left? Shifting left means that reactants were produced and the reaction occurred in the reverse direction. When the reaction shifts left, we will have 2 XY molecules breaking apart to form the reactants, 2 X molecules and 1 Y₂ molecule. We know this by looking at the reaction and seeing that 2 XY molecules react in the reverse reaction to form 2X and 1Y2. Therefore, the reverse reaction will lead to the production of this amount of reactants. This can be represented by drawing the following:
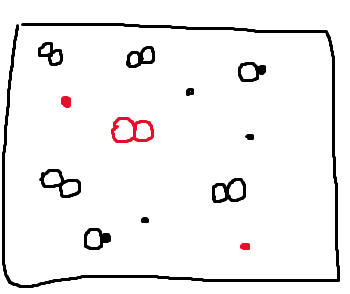
The red particles are the new molecules that we have formed from the breaking up of 2 XY molecules. If you compare the time one box to our new particulate diagram, you will see that we removed 2 XY molecules to form two new 2 X and Y₂ molecules.
If you think about it, all of this is conserving the law of conservation of mass, which states that the total mass of a closed system remains constant over time. Essentially, no matter can be created or destroyed.
Particulate Representations on the AP Exam
You may be thinking about how often this concept is tested on the AP exam since most of this unit focuses on mathematical representations of equilibrium. On the AP exam, you will be calculating lots of equilibrium constants and putting your knowledge of ICE tables to use to calculate concentrations.
In the coming sections, we’ll use new theories to make both qualitative and quantitative analyses of equilibrium. This unit is in a way “squished” in between these two topics as a reminder that equilibrium does not have to be strictly math! In fact, understanding equilibrium conceptually is a super powerful tool because not only does it mean the formulas and math will make more sense, but it also means that you’ll be able to properly explain your answers which is invaluable on FRQs. The College Board also loves to test conceptual knowledge on equilibrium on MCQs where they can give separate answers for a question. You may also see particulate representations in FRQs where, like in part (b) of our practice question, you will be asked to draw a new solution based on a reaction or shift in equilibrium. This section usually goes overlooked, but in fact it’s one of the most important in understanding the concepts of equilibrium!
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
🧐Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.