Dylan Black
Jillian Holbrook
AP Chemistry 🧪
269 resourcesSee Units
Unit 8 already covered the basics of acid-base chemistry and how to find the pH/pOH of solutions of strong acids and bases. However, the vast majority of acids and bases are, in fact weak, (remember, there are only seven strong acids as far as AP Chemistry is concerned)! In this section, we will discuss the difference between strong acids/bases and weak acids/bases, using equilibrium to find the pH of solutions with weak acids and bases.
Differentiating Strong Acids and Weak Acids
As we learned in Topic 8.1, there are two definitions of acids and bases: the Arrhenius definition, which states that acids yield H+ in water and bases yield OH-, and the Bronsted-Lowry definition, which broadens the scope to define acids and bases as proton "donors" and "acceptors" respectively. For the examples we discuss in this section, we will use the Arrhenius definition to exclude water as a sort of spectator to these reactions, but remember that behind the scenes, water is the backbone of why acids and bases can do what they do!
A strong acid or strong base is one that completely dissociates in water and does not return back to its product form. Or, at the very least, it does so to a negligible degree. For example, HCl is one of our seven strong acids that must be memorized. As a strong acid, it completely dissociates meaning that in solution, essentially all of the HCl molecules will dissociate into H+ (that is what makes it an acid!) and Cl-, the conjugate base. Strong bases to know are alkali and alkaline metal hydroxides, such as NaOH, Ca(OH)2, and Sr(OH)2.
It is also worth noting that when discussing strong acids and bases, although their conjugates are called conjugate bases and acids, respectively, they are not significant acids and bases. For example, although Cl- is the conjugate base of HCl, because HCl is such a strong acid, Cl- is an incredibly weak base to the point of not even being considered basic whatsoever. Similarly, when looking at a strong base like NaOH, it will fully dissociate into Na+ and OH-. Because NaOH is a strong base, Na+ is an incredibly weak acid, so weak that we do not even refer to it as an acid despite being a conjugate acid of NaOH.
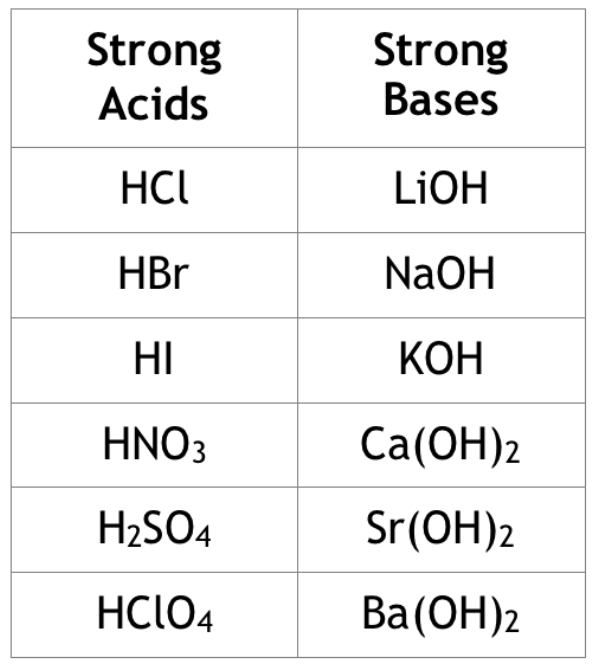
On the other hand, weak acids and weak bases incompletely dissociate in water. That is to say, not all of the acid/base will dissociate to yield H+/accept OH-. For instance, CH3COOH, acetic acid, is a weak acid with a Ka = 1.8 * 10^(-5).
We will talk a bit more about Ka in a future section, but a lower Ka corresponds to a weaker acid (in reality, it is the equilibrium constant for the dissociation of a weak acid, but we'll get there, don't worry 😉). This means that when dissolved in water, some CH3COOH will dissolve to form CH3COO- (the conjugate base) and H+, but much more of it will remain CH3COOH at equilibrium.
Any acid that is not one of the seven strong acids is a weak acid. As far as bases go, the only weak base you should be familiar with off the top of your head is ammonia (NH3), but you could face others on the AP exam (you will just be made aware by the question that it is weak!)
Review of General Equilibrium
As we move into discussing the relationship between weak acids, weak bases, and equilibria, let's do a quick refresher on some big key concepts from Unit 7, which was all about equilibrium.
Equilibrium is the state in a reaction in which the forward reaction and backward reactions are proceeding at the same rate, meaning that the production of products and reactants perfectly cancel each other out.

Equilibrium does not mean nothing is happening. There is just no more change in the concentrations of reactants and products. The above image is a graphical representation of equilibrium occurring. To mathematically represent the extent to which a reaction goes forward, we use the equilibrium constant, K.
In general, K is the ratio of the concentrations of the products raised to their stoichiometric coefficients and the concentrations of the reactants raised to their stoichiometric coefficients:
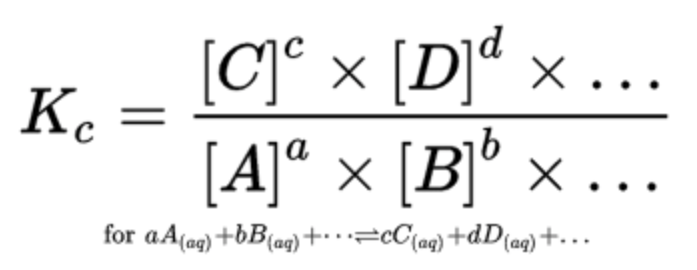
When finding equilibrium concentrations, we oftentimes use an ICE (or RICE) box to represent changes in concentration at equilibrium and then plug it into our K expression to solve. This is a strategy that we will also employ when dealing with weak acids and weak bases.
Weak Acid-Base Equilibria
Weak Acid and Base equilibria are just further examples of using equilibrium! Many students get tripped up because of some new symbols. In reality, it is the same as applying equilibrium to any other reaction (minus taking a few extra steps to find things like pH).
Let's take a look at an example:
- Find the pH of a 2M solution of CH3COOH (Ka = 1.8 * 10^(-5))
First, we write out the equation for the dissolution of acetic acid:
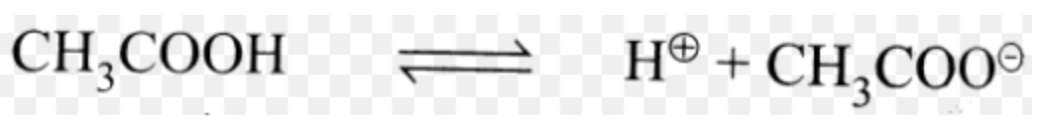
This expression (generalized as HA <=> H+ + A) is sometimes called the Ka expression for the acid.
The reaction above will guide us as we use the data above to find our [H+] and then take the -log() of that concentration. We are told that the Ka of CH3COOH is 1.8 * 10^(-5), a number we can use to create an ICE box and solve for [H+]:
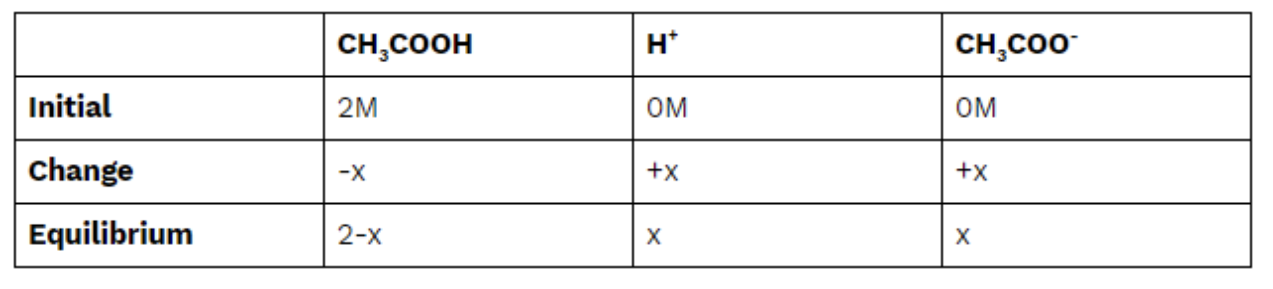
Finally, we plug in and solve for [H+]. Remember, because x is super tiny, we can assume that 2-x=2 to ease calculations:

Finally, taking the -log([H+]), we find that pH = 2.22.
Let's look at an example with a weak base:
- Find the pH of 1M ammonia (NH3). (Kb = 1.8 * 10^(-5)) (note: this is just a coincidence that this is the same as the Ka of Acetic Acid!)
Like before, we will start by writing out the Kb expression of Ammonia (the reaction of the weak base with water):

We know our Kb, so let's get ICE boxin! 💪

Same as before, we plug into our equilibrium expression to find x:
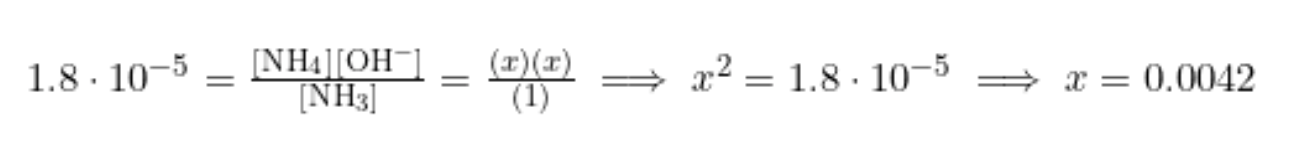
We may think we are home free. Just take the -log() of x, and we are done, right?! However, take a closer look. The -log() of x would not give us pH! Instead, it would give us pOH. To find pH, we first have to take pOH and then plug it into pH + pOH = 14.
pOH = -log([OH-]) = -log(0.0042) = 2.38
14 - 2.38 gives us a pH = 11.62.
Browse Study Guides By Unit
⚛️Unit 1 – Atomic Structure & Properties
🤓Unit 2 – Molecular & Ionic Bonding
🌀Unit 3 – Intermolecular Forces & Properties
🧪Unit 4 – Chemical Reactions
👟Unit 5 – Kinetics
🔥Unit 6 – Thermodynamics
⚖️Unit 7 – Equilibrium
🍊Unit 8 – Acids & Bases
🔋Unit 9 – Applications of Thermodynamics
🧐Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.