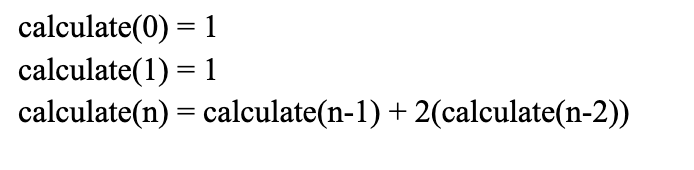AP Computer Science A 💻
130 resourcesSee Units
Answers and Review for Multiple Choice Practice on Recursion
Image From Wikipedia.
⛔STOP!⛔ Before you look at the answers make sure you gave this practice quiz a try so you can assess your understanding of the concepts covered in unit 10. Click here for the practice questions: AP CSA Unit 10 Multiple Choice Questions.
Facts about the test: The AP Computer Science A exam has 40 multiple choice questions and you will be given 90 minutes to complete the section. That means it should take you around 34 minutes to complete 15 questions.
*The following questions were not written by CollegeBoard and although they cover information outlined in the AP Computer Science A Course and Exam Description the formatting on the exam may be different.
1. What are the main aspects of a recursive method?
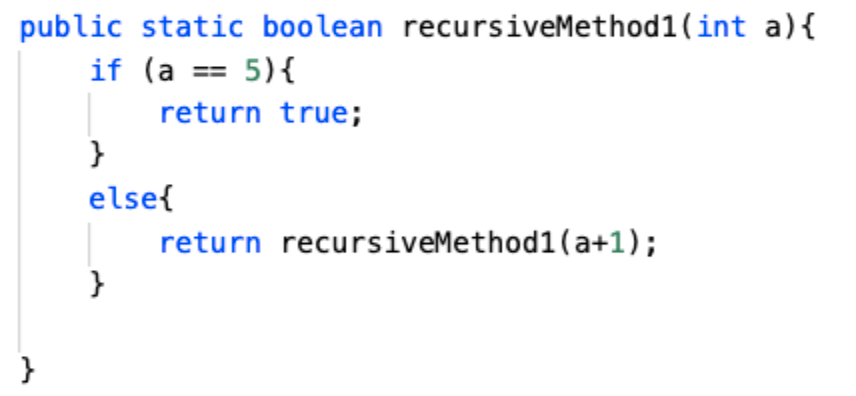
A. I
B. II
C. I, II
D. II, III
Answer: basic knowledge of a recursive method: includes a base case and a recursive part that calls the method itself
📄 Study AP CSA, Unit 10.1: Recursion
2. Which of these is the correct way a recursive method should call itself (Given the code below)?
A.
B.
C.
D.
Answer: The way to call a method still remains the same, no matter if a method is recursive or not. It should still be methodName(parameters); Therefore, recursiveMethod() in this case is the correct way to call itself.
📄 Study AP CSA, Unit 10.1: Recursion
3. Which method is not recursive?
A.
B.
C.
D.
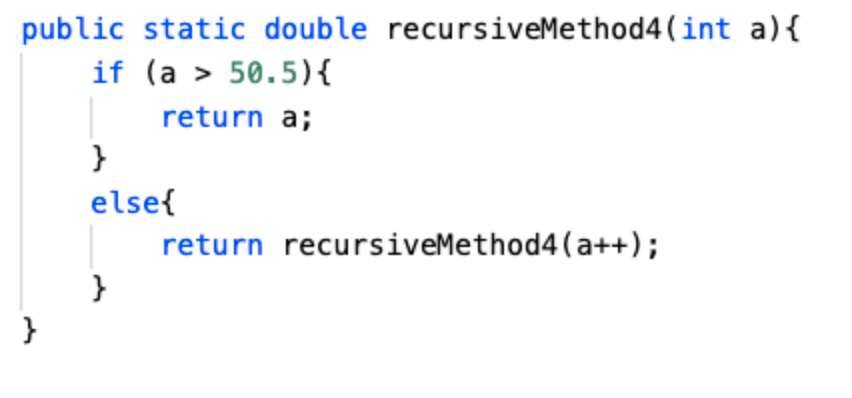
Answer: Definition: The method recursiveMethod4() does not make a call to itself, which means that it is not recursive. The rest of the other 3 methods all make calls to themselves, making them recursive methods.
📄 Study AP CSA, Unit 10.1: Recursion
4. Given the recursive method below, what will be printed out if the method is called: printing(492); ?
A. 492
B. 984
C. 984984
D. 9849849
Answer: When 492 is given as a parameter to printing(), it first prints out val*2, which is 984. Then, it checks if val%2 ==0, and 492%2==0, as it's an even number so it has no remainder when divided by 2. Next, the recursive part occurs as printing is called with the value this time beign val/10, which is 49. This time, 98 is printed out. Then, val%2==0 is checked, which is false this time since 49 is an odd number so the remainder is 1, not 0, so it goes to else, which prints out 49. Therefore, 9849849 is printed out.
📄 Study AP CSA, Unit 10.1: Recursion
5. Given the recursive method below, what will be returned out if the method is called in findNumberX("xjxfeixx"); ?
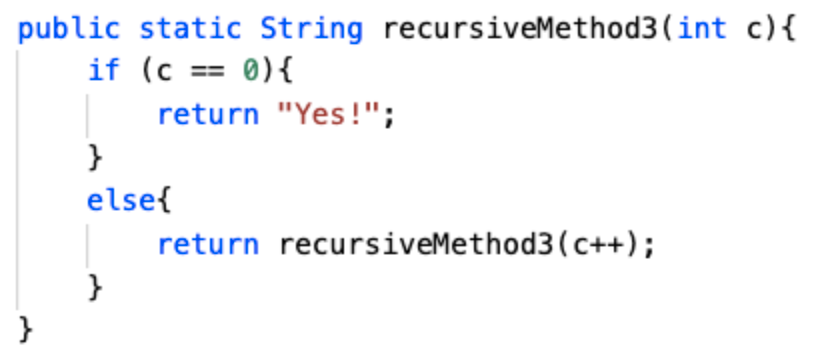
A. 0
B. 3
C. 4
D. 5
Answer: The recursive method finds the number of x's, by checking the first character of the String passed in and then calling itself again with the first character of the String removed. This method finds 4 x's in the String "xjxfeixx" passed in.
📄 Study AP CSA, Unit 10.1: Recursion
6. How does binary search work?
A. Binary search sorts an array by dividing the given list in half, and repeating that process until it finds the target value.
B. Binary search sorts an array by checking every value in the list until it reaches the target value.
C. Binary search sorts an array by comparing a value to the already sored values and shifting it to fit it in where it belongs.
D. Binary search sorts an array by moving items in an unsorted list into a sorted list one at a time and swapping numbers one at a time with elements in the sorted list.
Answer: Definition of Binary search.
📄 Study AP CSA, Unit 10.2: Recursive Searching and Sorting
7. Which type of sort is usually the quickest?
A. Selection Sort
B. Merge Sort
C. Insertion Sort
D. Linear Search
Answer: Merge sort is usually the quickest method because it works much like binary search and separates the values in half to sort.
📄 Study AP CSA, Unit 10.2: Recursive Searching and Sorting
8. Which of these recursion methods results in an infinite recursion if the value of a passed in to all of them is -1?
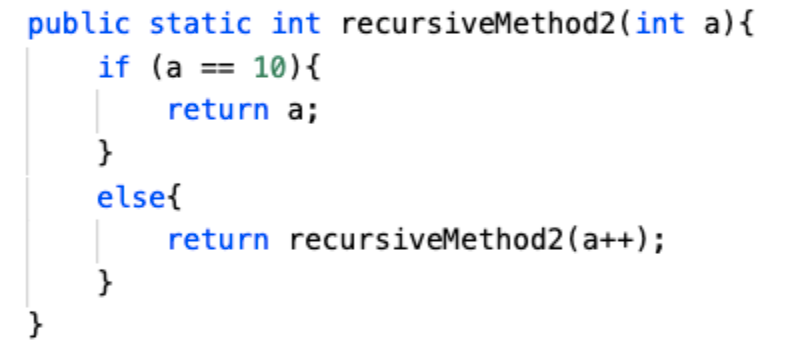
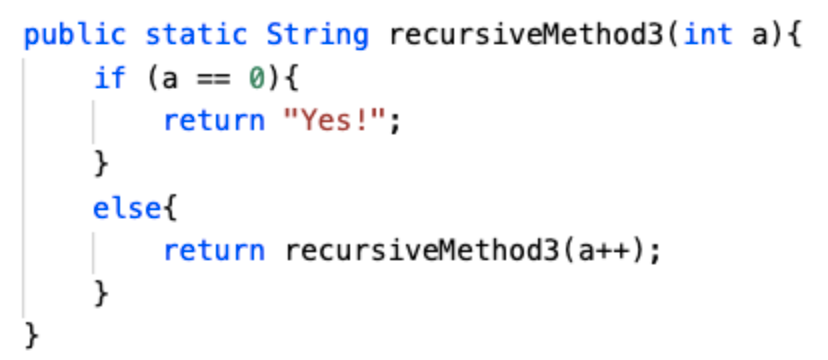
A.
B.
C.
D.
Answer: a), recursiveMethod1() results in an infinite recursion if the value passed in is -1. This is because the if statement, which is the condition that breaks this infinite recursion, occurs only when a is greater than 5. a starts off with a value less than 5, and the else statement that calls the method itself again provides a value of a--. This means that no matter how many times this method is called within itself, the value of a continously decreases, meaning that it never reaches the if statement of a > 5.
📄 Study AP CSA, Unit 10.1: Recursion
9. Where is the recursive call?
A. 3
B. 5
C. 6
D. 7
Answer: Definition: The recursive call is the same line of code where the method itself is called.
📄 Study AP CSA, Unit 10.1: Recursion
10. Given the recursive method below, if the value passed in is 4444, what is printed out by the method?
A. 4444
B. 88884444
C. 8888444422221111
D. Infinite Recursion
Answer: 4444 is an even number, which means that it will satisfy the if statement, and then the infinite recursion part begins as 4444 will be multiplied by 10, remaining an even number, continuously increasing the value every time and getting into an infinite recursion.
📄 Study AP CSA, Unit 10.1: Recursion
11. Given the recursive method below, how will the method return a boolean value of true?
A. The String str has to start with at least 3 of the same characters in a row.
B. The String str has to contain at least 3 of the same characters in a row.
C. The String str has to end with at least 3 of the same characters in a row.
D. The String str has to contain at least 3 of the same characters.
Answer: The recursive method result() compares a String, and the str.length() == 3 makes sure that the length of the remaining string is at least three in a row, then the substring calls compare three characters in a row in the string to confirm if they're the same. The recursive call just moves through the entire string if three characters in a row aren't found in the String
📄 Study AP CSA, Unit 10.1: Recursion
12. Given the recursive method below, what will be returned if the method is called: remainder(18); ?
A. 0
B. 1
C. 2
D. 3
Answer: Since 18 isn't equal to 0, we move to the else statement. r is 2, as the remainder of 18/4 is 2. Then, the recursive part occurs. 18/4 rounds down to 4. The remainder of 4/4 is 0, which is r. Then, 4/4 = 1, which is passed in again. The remainder of 1/4 is 1. 1/4 = 0. Now, the value passed in is 0, meaning that the method returns 0, and the previous values are added up: 2+0+1=3.
📄 Study AP CSA, Unit 10.1: Recursion
13. If given the following, n = 3, what is the answer?
A. 0
B. 1
C. 2
D. 3
Answer: Since calculate(3) = calculate(2) + 2(calculate(1)), we can simplify calculate(2) to calculate(1) + 2(calculate(0)). This gives us calculate(3) = calculate(1) + 2(calculate(0)) + 2(calculate(1)). Given that calculate(0) = 0 and calculate(1) = 1, we can plug in values to get calculate(3) = 1 + 2(0) + 2(1), which simplifies to calculate(3) = 1+2 = 3.
📄 Study AP CSA, Unit 10.1: Recursion
14. What common error can recursive methods cause (not limited to recursive methods)?
A. StackOverflowError
B. IndexOutOfBoundsError
C. InterruptedException
D. RuntimeException
Answer: Too many recursion calls may cause the stack to be full, meaning that more methods cannot be called, hence the StackOverflowError.
📄 Study AP CSA, Unit 10.1: Recursion
15. To simulate the Fibonacci sequence or factorials, what is typically used?
A. Iteration
B. Recursion
C. Loops
D. None of the Above
Answer: Definition: The Fibonacci sequence and factorials rely on knowing previous values, and calling the method itself makes it easier to repeat this process until the base case is met.
📄 Study AP CSA, Unit 10.1: Recursion
What can we help you do now?
🤝 Connect with other students studying AP [Name] with Hours
Browse Study Guides By Unit
➕Unit 1 – Primitive Types
📱Unit 2 – Using Objects
🖥Unit 3 – Boolean Expressions & if Statements
🕹Unit 4 – Iteration
⚙️Unit 5 – Writing Classes
⌚️Unit 6 – Array
💾Unit 7 – ArrayList
💻Unit 8 – 2D Array
🖲Unit 9 – Inheritance
🖱Unit 10 – Recursion
🙏Exam Reviews
Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.