📚

All Subjects

⌨️

AP Comp Sci P

⚙️

Unit 2

Binary Numbers

8 min read•january 3, 2023

Milo Chang

AP Computer Science Principles ⌨️

80 resources

See Units

In its simplest form, data is a collection of facts. You can collect data from all sorts of mediums, from lab experiments and sensors to photos and videos. It's used in almost every profession and makes up a big part of the world around us.

As we've discussed before, computers run on data, but how do these computing devices store this data?

There are many different ways to answer this question. You've seen how data can be stored in spreadsheets and charts for humans to use. When coding, data is also stored in variables, lists, or as a constant value for programs to work with. (We'll discuss variables, lists, and constants more in the next guide!)

At their core, computers store data in bits, or binary digits.

Before we talk about how binary is used, we first have to understand what it is and how it works. To do that, we need to talk about number bases.

Number Bases

A number base is the number of digits or digit combinations that a system uses to represent values.

Most of the time, we work with the decimal system (also known as base-10) which only uses combinations of 0-9 to represent values.

However, computers function using machine code, which generally uses the binary system (also known as base-two).

The binary system only uses combinations of 0 and 1 to represent values, and can be a little difficult to understand at first.

If we think way back to elementary school, we'll remember the place value system that the decimal system uses. There's the ones' place, then the tens' place, then the hundreds' place and the thousands' place—and so on.

For example, take the number 5,729. This number has a 5 in the thousands' place, a 7 in the hundreds' place, a 2 in the tens' place and a 9 in the ones' place. That means that 5,729 is made up of 5 thousands + 7 hundreds + 2 tens + 9 ones.

Here's a chart demonstrating this system:

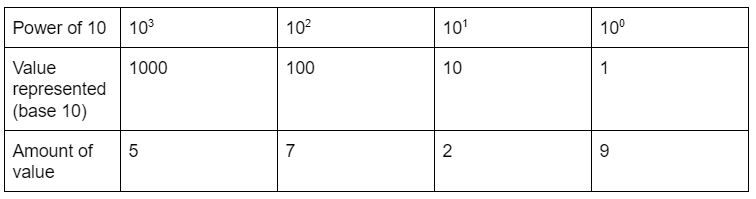
Each place value represents a different power of ten and can only hold a value of up to 9. After that, the place reverts to zero, and the next place up increases by 1. For example, if you add 1 to 9, the number becomes 10, with a 1 in the tens' place and a 0 in the ones' place. If you add 1 to 29, the number becomes 30: the tens' place increased by a value of 1.

In the binary system, each place can only hold a value of up to 1. The name of the place values also changes because of this. The system goes from the ones' place to the twos' place to the fours' place to the eights' place—and so on.

Let's look at an example of how we'd represent a value in binary, using the number 5.

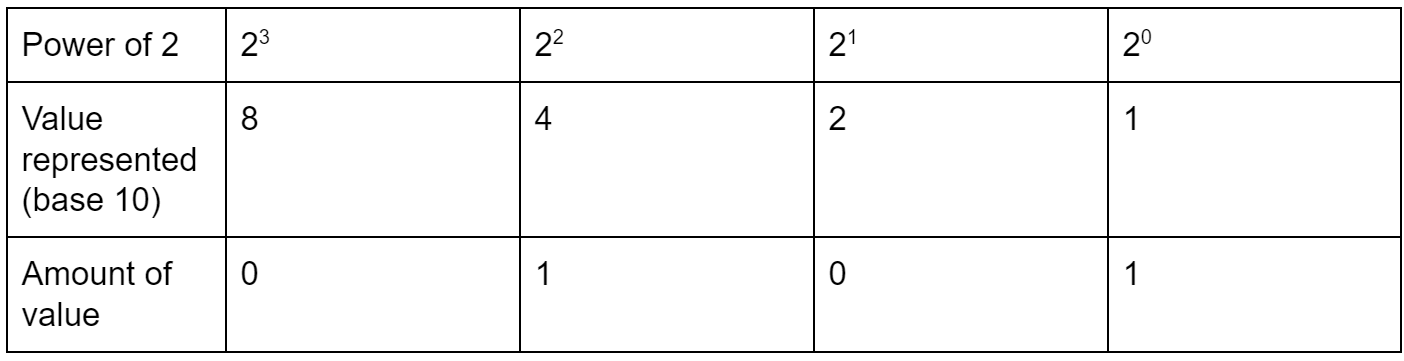
The binary number 0101 has a 1 in the fours' place and a 1 in the ones' place, which means that the number represented is made up of 1 four plus 1 ones, or 4 + 1, which = 5.

These binary digits are also known as bits. If you put eight of these bits together, you get a byte.

Nom nom nom... Image source: GIPHY

These binary strings can get rather long rather quickly. In order for *people* (not computers, which use binary!) to work with these values more easily, they use the hexadecimal, or base-16 system. A good example of this are the RGB color codes, which are written in hexadecimal.

The hexadecimal system uses both letters and numbers to represent values. You represent 0-9 as you would in the base-10 system, but then you use the letters A to F to represent 10-15. The place values change as well, to multiples of 16.

Let's use the number 5,729 again and represent it using the hexadecimal system.

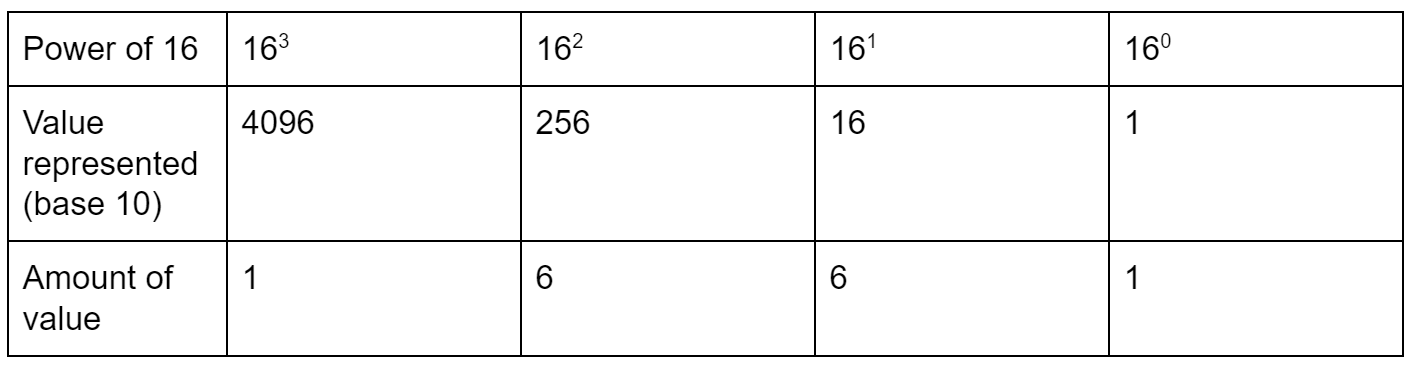
This number is made up of one 4096 + six 256s + six 16s + one 1, which totals to equal 5,729.

The AP CSP test may ask you to perform conversions from binary to base ten and hexadecimal. For more information about how to do these conversions, see the Exam Guide.

Bit Representations

Bits are used to represent everything you see and work with on a digital screen, including numbers, colors, and even sound waves!

The same sequence of bits can represent different types of data depending on the context.

For example, take this chart representing the ASCII code, the foundation of the modern Unicode system that converts text to binary format.

Image source: ZZT32 / Public domain

As you can see, the binary representation for the capital letter "A" could also be used to represent the number 65.

Fortunately, programs are designed to know what the binary value they're reading is meant to represent, and there usually aren't mix-ups. However, it's important to have consistent communication standards between different programs and computers, to prevent any possible confusion.

🔗 Check out this super cool video from TED-Ed about how Binary works!

So if binary is the language that computers use, why aren't we constantly dealing with these zeros and ones when we use our devices? The answer lies in a concept known as abstraction.

Abstraction

Abstraction is the process of reducing complexity by focusing on only the ideas that a user needs to know. This is done mainly by hiding irrelevant details from the user.

How does this work?

A non-computer science related example of abstraction is pressing the "start" button on your oven. You don't have to know how the oven works to use it. You also don't have to deal with all the little details of starting the oven, such as turning on the gas or controlling the fans inside. The start button is an abstraction because it only focuses on the main idea of the task you're trying to accomplish: beginning the heating process.

You don't need to know how your oven works to make these delicious cookies, only that it does. Image source: GIPHY

This same concept applies to your computer. Your computer stores data in bits, but programs running on your computer interpret it through variables and lists and can then display it through spreadsheets and charts.

It does this because it's difficult for humans to understand a string of zeros and ones. You also don't need to understand these strings in order to use your computer or code a program.

Just like how the start button hides all the specific details of running an oven, code statements and screen displays hide the internal processes of a computer, including its binary representations.

Analog Data and Bit Representations

Analog data is data that is measured continuously. Its key characteristic is that analog data values change smoothly, rather than in discreet intervals.

For example, imagine that you're listening to a flute solo your friend is playing, and you're at a part where the music is getting louder and louder. The volume of the music is changing smoothly and would be considered an example of analog data.

Other examples include the time recorded on an analog clock or the temperature measured on a physical thermometer, like the one pictured below.

Image source: Jarosław Kwoczała on Unsplash

In both of these devices, data is being recorded constantly: the clock hands and thermometer mercury are (at least in theory) always moving.

Now, let's say you wanted to measure all of this data (the volume of the flute music, the temperature of a room, the current time) digitally, using a device like a sound recorder. Once collected, this information would be known as digital data.

Analog data can be represented digitally by using a sampling technique. The values of the analog signal are measured and recorded at regular intervals. (The intervals are known as samples.) These samples are then measured to figure out how many bits will be needed to store each of them.

Digital data must be formatted in a finite set of possible values, while analog data can be infinite. Think about a (basic) digital clock, for example. It only changes every minute, as opposed to the constantly changing hands of an analog clock. Another example would be watching a video of an event versus watching the event in person: when you watch the video, you're watching a large number of images put together. In contrast, the event is happening continuously when you're at the venue.

This divide between continuous and finite means that digital data, while it can come very close, can only be used to approximate analog data rather than perfectly represent it.

Digital data is a simplified representation that leaves out extra details. Going back to the digital clock example, you usually don't need to know the time down to the millisecond; oftentimes, the hour and minute are enough.

Due to this simplification, using digital data to approximate real-world analog data is considered an example of abstraction.

Overflow Errors

In many low-level programming languages, such as C and C+, numbers are represented by a certain number of bytes (anywhere from one to eight). This limits the range of values and operations that can be done on those values.

Let's say that a number is represented by one byte, or eight bits.

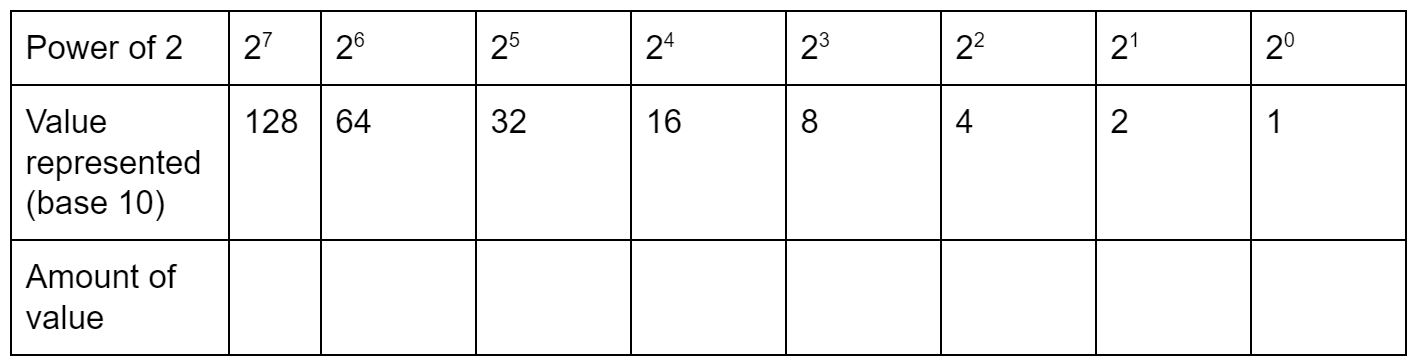
Here's a chart representing a byte, or eight bits.

❓ What's the maximum value this byte can store?

The byte can represent (128 + 64 + 32 + 16 +8 + 4 + 2 + 1). If you add the numbers all up, you get 255 in base-10, represented as 1111 1111.
The easier way to calculate this value is to go to the next power up from the last one on the chart—In this case 2 to the 8th, which is 256—and then to subtract one.

What if you tried to represent 256 or higher on this chart? You can't because there's no way to store the value. Trying to store a larger number would lead to an overflow error.

This overflow error may present itself in several ways. The number may display negative when it should be positive, or vice versa. It might also display a completely different value, such as 0. Overflow errors don't usually cause the program to stop working, so they can be hard to detect.

Higher-level programming languages, such as Python, work around this problem and remove the range limitation. In such languages, the largest number you can represent depends solely on how big your computer's memory is! (The AP CSP test also uses this standard.)

Another way that number storage makes use of abstraction is through rounding. Because you have a limited amount of bits to store numbers, the computer will sometimes round or cut off your number. This can be most prominently seen when you're working with very small numbers or repeating decimals.

Here's a basic dividing program I wrote on my computer in Python. As you can see, the answer to 100/3 has a finite end in the program, even though it's meant to be a repeating decimal.

This is an example of abstraction because the number represented by the computer is a simplified version of the full value. Although it usually doesn't matter for most calculations, including the ones you'll do in school, rounding or round-off errors can sometimes cause issues if you need more precision.

Browse Study Guides By Unit

🕹Unit 1 – Creative Development

⚙️Unit 2 – Data

2.0Multiple Choice Questions

2.1Intro to Big Idea 2: Data and Binary Numbers

2.2Data Compression

2.3Extracting Information from Data

2.4Using Programs with Data

📱Unit 3 – Algorithms & Programming

🖥Unit 4 – Computer Systems & Networks

⌨️Unit 5 – Impact of Computing

✏️Frequently Asked Questions