J
Jeanne Stansak
dylan_black_2025
AP Microeconomics 🤑
95 resourcesSee Units
The Theory of the Firm
Microeconomics is roughly split up into two main sections: consumer theory and producer theory. Unit 3 has focused broadly on producer theory, the theory by which economists attempt to understand how firms act in certain markets. The primary theory of producer theory that we focus on in AP Microeconomics is the theory of the firm. This theory argues that the primary goal of any firm, regardless of market structure, is to maximize profits. This is done in all market structures through the same profit maximizing rule, which is the focus of this guide.

The average firm in AP Microeconomics...it's all about the cash money
MR = MC: The Profit Maximizing Rule
The profit maximizing rule is one of, if not the most important equation in AP Microeconomics. It will define most of the actions of a firm for this course. The profit maximizing rule is as follows: a firm has its profits maximized at the quantity where MR = MC. The logic of this is pretty similar to other marginal analyses.
A firm can exist in one of three positions:
MR > MC, MR < MC, or MR = MC.
When MR > MC, the firm has the potential to earn more marginal profit (MR - MC > 0) for the next product it produces. This means it should keep producing units while MR > MC.
When MR < MC, the firm actively loses profits by producing an additional unit, so a firm should scale back production.
We equilibrate at the point where MR = MC, where we've exhausted all available quantities where MR > MC, but haven't lost any profit by expending more than we make. Thus, profit is maximized when MR = MC.
This can be seen in the following graph. The red line represents total cost, and the slope of that total cost represents marginal cost. The blue line represents total revenue, where the slope is marginal revenue. Note that were profit (notated as π) is maximized when these slopes are the same. When MR != MC, the two curves are moving towards each other, meaning profit is approaching zero.
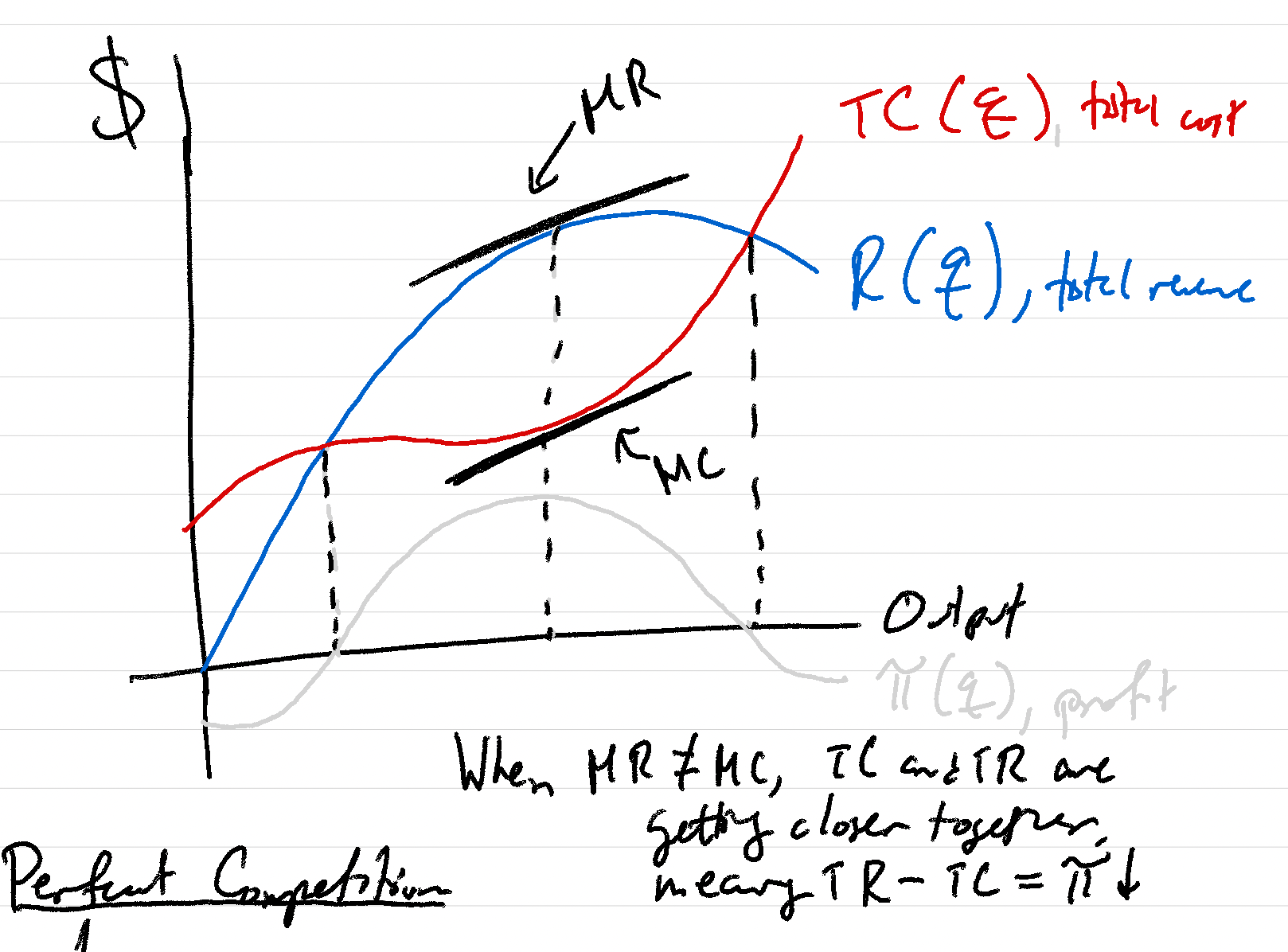
Example
In economics, we refer to the profit-maximizing point as the quantity where marginal revenue (MR) equals marginal cost (MC). When we produce at this quantity, the costs of producing the last unit of output equals the revenue gained when selling it.
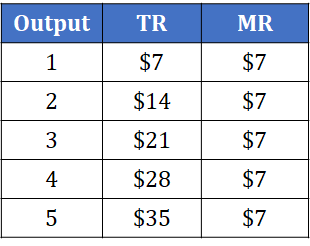
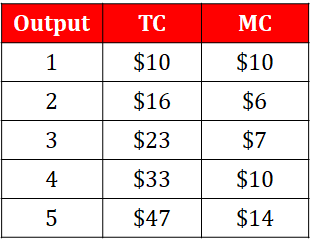
In the tables below, you can see that at 3 units, MR = MC ($7 = $7). This would be considered the profit maximization point for this firm. The firm will not produce a quantity lower than 3 because they would be producing a quantity where MR > MC, which means that the firm has the potential to earn more revenue per unit and is not maximizing its profits. They would also not produce above the quantity of 3 because if they did they would be producing at a point where MC > MR, which means the additional cost of producing each additional unit is more than the revenue it earns for the firm, incurring a loss.
Revenue for Firm B
Costs for Firm B
Browse Study Guides By Unit
💸Unit 1 – Basic Economic Concepts
📈Unit 2 – Supply & Demand
🏋🏼♀️Unit 3 – Production, Cost, & the Perfect Competition Model
⛹🏼♀️Unit 4 – Imperfect Competition
💰Unit 5 – Factor Markets
🏛Unit 6 – Market Failure & the Role of Government
🤔Exam Skills
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.