3.7 Free-Body Diagrams for Objects in Uniform Circular Motion
5 min read•june 18, 2024
Peter Apps
Kashvi Panjolia
AP Physics 1 🎡
257 resourcesSee Units
Free Body Diagram Basics
As you already know, a free body diagram (FBD) is a visual representation of the forces acting on an object. It is a powerful tool that can be used to analyze the motion of an object, such as an object undergoing uniform circular motion. When drawing a free body diagram for an object in uniform circular motion, it is important to select an appropriate coordinate system and to accurately represent the forces acting on the object.
Free body diagrams can be drawn in two ways: 1) by representing the object as a point mass and drawing arrows pointing outward from the dot to represent the forces acting on an object and 2) by drawing the forces on an object specifically at the point where they are exerted on the object. In this guide, we will use the first way of drawing FBDs. An example of the second way of drawing the free body diagram could be a box sliding on a frictional surface.
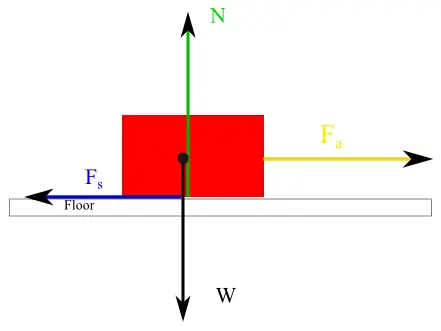
Image courtesy of PhysicsProblems.
In this image, the force of static friction is acting at the point where the box meets the floor, and that is where it is drawn. The weight of the box (W) is acting at the center of mass of the box, where the weight force always acts on an object. The normal force of the floor on the box is acting at the point where the box meets the floor. The applied force (F_a) on the box could be a rope that is pulling on the box at the center of its right side, which is why the applied force vector is placed on the right side of the box. Drawing a free body diagram for an object this way can be useful to more specifically analyze the motion of an object.
FBDs for Uniform Circular Motion
The first step in drawing a free body diagram for an object in uniform circular motion is to select an appropriate coordinate system. Your positive x or y axis should always be in the direction of the centripetal force, toward the center of the circle. From there, you can create your coordinate system and break down any forces that are not aligned with your coordinate system into x and y components. The centripetal force will always point toward the center of the circle, but you may be surprised to find that the gravitational force will not always point downwards. For example, in the case of a planet orbiting the sun, the gravitational force is the centripetal force, so it will point towards the center of the circle no matter where in the orbit the planet is.
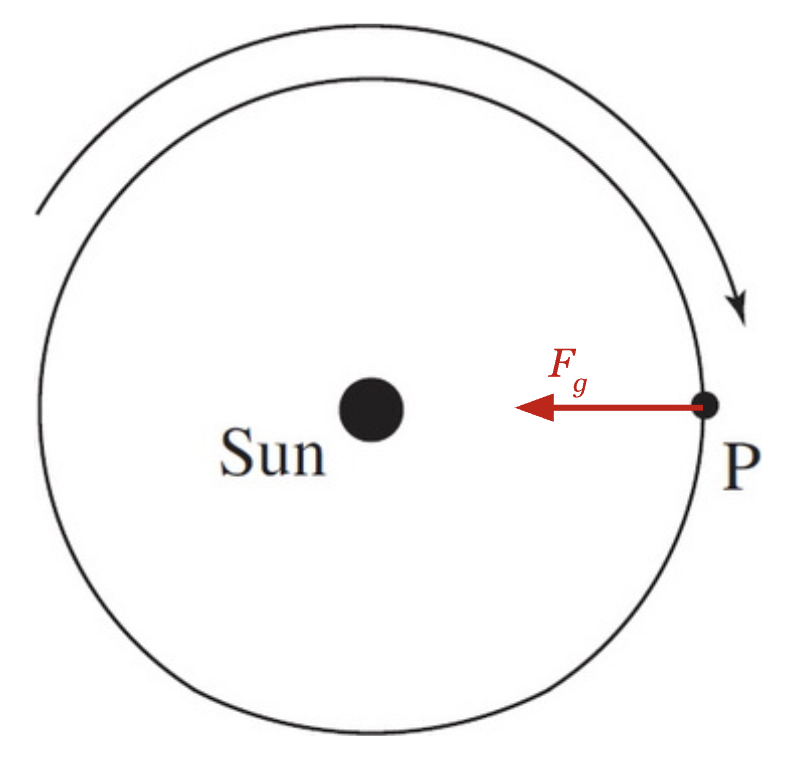
Image courtesy of CrackAP.
Here, the gravitational force points to the left in our frame of reference. It is the only force keeping the planet in its orbit, so it is also the net force.
When drawing the free body diagram, it is also important to consider any other forces that may be acting on the object. For example, if the object is moving in a circular path on a frictionless surface, there will be no friction force acting on the object. However, if the object is moving in a circular path on a surface with friction, a frictional force will be acting on the object opposing its motion. It's important to consider all the forces acting on the object, including contact forces such as tension, friction, and normal force, and non-contact forces such as gravity.
Roller Coaster FBD

Imagine the colored rectangles above depict a roller coaster at different points during a loop-the-loop. Red represents the top of the loop, orange represents the right, green represents the left, and yellow represents the bottom. Let’s practice free-body diagrams for uniform circular motion by drawing one for each position of the roller coaster.
Remember, since we are in uniform circular motion where the tangential velocity is constant, there is only centripetal acceleration, no tangential acceleration. If there is a centripetal force causing centripetal acceleration, it must point to the center. The normal force of the track on the car is the only force in this scenario that points to the center. Normal force doesn't always point to the center; there are always exceptions! Solve each problem you encounter case by case - use your free-body diagrams!
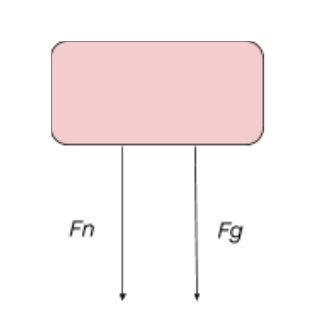
The free body diagram above depicts the roller coaster at the top of the loop, where the normal force and the force of gravity are both pointed downwards. Since the normal force is always perpendicular to the surface and acts on the object we are concerned with (the car), the normal force will point downwards at the top of the track. Also, the normal force causes the centripetal acceleration when you go on a loop-the-loop, so it is pointing towards the center, which in this case is vertically downwards. The gravitational force will be pointing vertically downwards in this scenario because we are on Earth's surface. This free body diagram gives us a net force equation of Fnet = Fn + Fg for a car at the top of the loop.
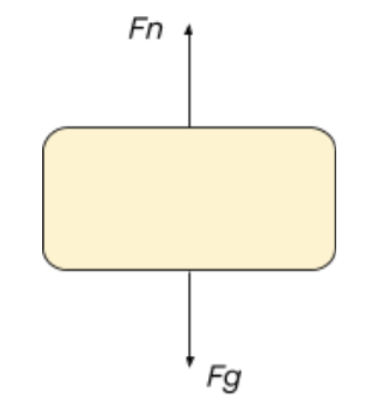
The free body diagram above depicts the roller coaster at the bottom of the loop, where Normal Force is pointed upwards, toward the center of the circle, and the gravitational force is pointed downwards. Although it is not depicted in the picture, the normal force is the net force on the car, so its magnitude is greater than that of the weight of the car to produce a net force.
Remember that the normal force contributes to the apparent weight of an object -- how heavy the object feels. Since the normal force is greater than the gravitational force, a person on the car at the bottom of the loop will feel heavier than they actually are. At the top of the loop, the normal force and gravity were pointing in the same direction, but since the centripetal acceleration in uniform motion is constant, the normal force actually had a smaller magnitude than the gravitational force. This means that at the top, the car (and the person in it) experienced an apparent weight that is less than their actual weight, so they felt lighter than they actually are.
The free body diagram for the bottom of the loop (in the image above) gives us a net force equation of Fnet = Fn - Fg.
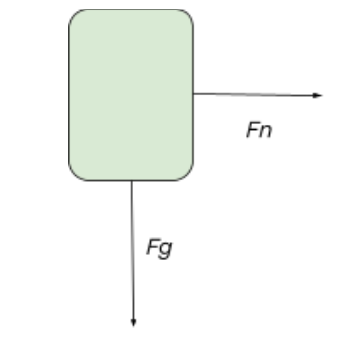
The free body diagram above depicts the roller coaster at the left of the loop, where the normal force is pointed rightwards, and the gravitational force is pointed downwards. Since the normal force is the only force pointing towards the center of the loop, we get a net force equation of Fnet = Fn.

The free body diagram depicts the roller coaster at the right of the loop, where the normal force is pointed to the left, and the gravitational force is pointed downwards. Since the normal force is the only force that is pointing in the direction of the centripetal acceleration, we get a net force equation of Fnet = Fn.
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
📚Study Tools
🧐Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.