Peter Apps
Kashvi Panjolia
AP Physics 1 🎡
257 resourcesSee Units
Learning Targets
A vector field gives, as a function of position (and perhaps time), the value of a physical quantity that is described by a vector.
Key Concept: Vector Field - the assignment of a vector to each point in a portion of space. A vector field can be visualized as a collection of arrows with a given magnitude and direction, each attached to a point in the plane. ⬇️

Image courtesy of Open University.
Uniform Circular Motion
As shown in the image above, a vector field can represent circular motion. This vector field shows the tangential velocity for an object in circular motion. The vectors are tangent to (make a 90 degree angle with) the circle and only touch the circle at one point. From this vector field depiction, we can go into more depth of the specific components of uniform circular motion.
Key Concept: Uniform Circular Motion - the motion of an object in a circle at a constant speed that is accelerating due to a change in direction.
Remember that there does not have to be a change in speed for there to be acceleration. Acceleration can be caused by a change in direction as well. A car making a turn at a constant speed is still accelerating because its direction is constantly changing. 🚗
In UCM there are four typical forces you will deal with: Tension, Friction, Gravity, and Normal. These forces are the cause of centripetal force. Centripetal force is not a new force; it is just a name for the force directed toward the center of the circle that is causing acceleration.
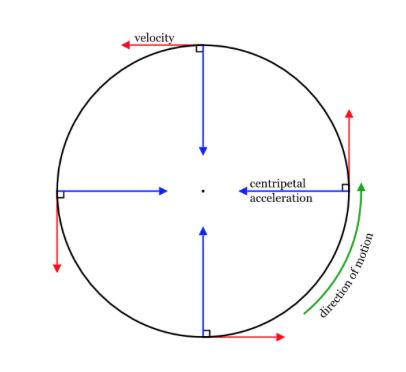
Image courtesy of Quizlet.
From this diagram, we can see that in uniform circular motion, centripetal acceleration is constant and always pointed towards the center, or center-seeking. Similarly, the centripetal force always points toward the center. However, velocity is tangent to the center; therefore, it is not considered in the net force. All forces pointing toward the center of the circle are positive (+), and all forces pointing away from the center of the circle are negative (-). Anything that doesn’t point away from or towards the circle’s center isn’t considered in the net force, and since the velocity is tangent to the circle, it is not considered in the calculation for net force.
- Key Concept: Centrifugal - moving or tending to move away from a center.
- Key Concept: Centripetal - moving or tending to move toward a center.
- Key Concept: Centripetal Force - a force that acts on a body moving in a circular path and is directed toward the center around which the body is moving.
It is important to note that the centrifugal force is not a real force. This is a common misconception held by many students. The centrifugal force is an apparent force that is observed in a rotating reference frame. It is the result of the inertia of an object moving in a circular path, which makes it seem as though there is a force pushing it away from the center of rotation.
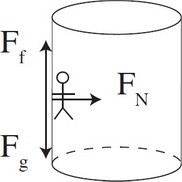
Image courtesy of CrackAP.
In this free-body diagram of a person spinning on an amusement park ride, there is no mention of a centrifugal force keeping the person pressed against the wall as the cylinder spins. The force of static friction keeps the person from sliding to the ground, and that is what causes the person to feel like they are stuck to the wall. The faster the ride spins, the greater the static friction force, and the greater the apparent gravitational force that pins you to the wall. The ride spins so fast that the force is greater than your gravity force and makes you feel pressed against the wall. 😵💫
Equation: Fc = mv^2/r, where Fc is Centripetal Force in Newtons, m is mass in kilograms, v is the velocity in m/s, and r is the radius in meters.
The centripetal force is the name for the net force. Let’s dive into how the equation for centripetal force is derived: Newton’s second law gives us the equation F =ma, which can also be adapted for net force. Acceleration in a uniform circular motion is given as a = v^2/r, so Centripetal Force is simply mass times v^2/r or mv^2/r. Remember not to include the centripetal force on any free-body diagrams because it is not a force, but rather the net force.
Vector Field Between Two Objects
The idea of using a field of vectors to represent the gravitational attraction between two objects is beyond the scope of AP Physics 1, so we use a simplified version of a vector field to represent this interaction.

Image courtesy of School for Champions.
This image displays the gravitational attraction between the Earth and the moon. You can see that the vector pointing left represents the gravitational force of the Earth on the Moon and the vector pointing right represents the gravitational force of the moon on the Earth. When we say that object A has a gravitational force on object B, we are saying that object A is pulling object B towards it.
The distance between the Earth and the moon is calculated using the distance between their centers of mass to simplify calculations. The two vectors are used to represent the magnitude and direction of the gravitational force between two objects.
🎥Watch: AP Physics 1 - Unit 3 Streams
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
📚Study Tools
🧐Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.