Unit 3 Overview: Circular Motion and Gravitation
9 min read•june 18, 2024
Peter Apps
Kashvi Panjolia
AP Physics 1 🎡
257 resourcesSee Units
Seemingly simple actions around us, such as car tires spinning or a satellite orbiting a planet, have much more complex processes at hand. In Unit 3, you will continue to build upon your understanding of the physical world using representations to form a more complete and complex model of motion as it relates to gravitational mass and inertial mass. Specific preconceptions will be addressed in this unit, such as the idea of a centrifugal force.
This unit makes up 4-6% of the AP exam, and it tends to span over approximately 7-9 forty-five minute class periods.

Image courtesy of makeameme.org
Applicable Big Ideas
Big Idea #1: Systems - Objects and systems have properties such as mass and charge. Systems may have an internal structure.
Big Idea #2: Fields - Fields existing in space can be used to explain interactions.
Big Idea #3: Force Interactions - The interactions of an object with other objects can be described by forces.
Big Idea #4: Change - Interactions between systems can result in changes in those systems.
Key Concepts
- Vector
- Vector Field
- Uniform Circular Motion
- Centripetal Force
- Centrifugal
- Gravitational Force
- Newton’s Universal Law of Gravitation
- Gravitational Field
- Gravitational Mass
- Inertial Mass
- Frame of Reference
Key Equations
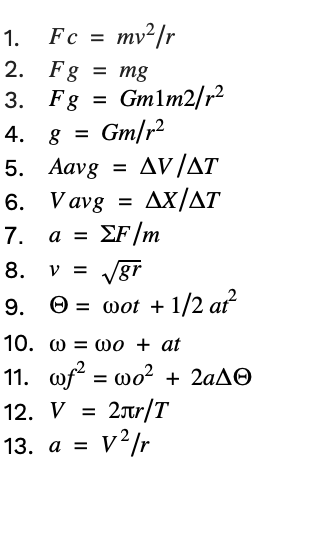
3.1 Vector Fields
Vector fields in physics are mathematical representations of a physical quantity that has both magnitude and direction. In the case of uniform circular motion, the vector field represents the velocity of an object moving in a circular path at a constant speed.
The vector field for uniform circular motion can be represented by a vector pointing in the direction of the object's motion, with its magnitude equal to the object's speed. The direction of the vector field changes as the object moves in its circular path, but its magnitude remains constant.
In addition to velocity, vector fields can also be used to represent other physical quantities such as force, acceleration, and magnetic fields. These vector fields can be visualized using arrows, with the direction and length of the arrow representing the direction and magnitude of the physical quantity.
The vector field between two objects is beyond the scope of AP Physics 1, so we simplify the vector field into a single vector. For example, the gravitational force between the Earth and the moon can be represented with two vectors:

Image courtesy of School for Champions.
This image shows how the Earth is pulling on the moon (the vector on the moon pointing left), but the moon is also pulling on the Earth (the vector on the Earth pointing right). However, the moon's pull on the Earth is much weaker than the Earth's pull on the moon, so the moon orbits around the Earth instead of the other way around.
3.2 Fundamental Forces
The four fundamental forces in physics are the gravitational force, the electromagnetic force, the weak force, and the strong force.
The gravitational force is the force of attraction between two masses. It is one of the weakest forces in nature, but it dominates at large mass and distance scales, such as the orbits of planets and galaxies. The electromagnetic force is the force that mediates the interactions of electrically charged particles. It is one of the strongest forces in nature and is responsible for phenomena such as electricity, magnetism, and light. The weak force is the force responsible for certain types of radioactive decay, such as beta decay. The strong nuclear force is the force that holds the protons and neutrons in the nucleus of an atom together. It is the strongest of the four fundamental forces and is responsible for phenomena such as nuclear fusion and fission. For the purposes of AP Physics 1, only need to understand the gravitational force in depth.
Gravity is a long-range force because its effects can be felt over large distances. Unlike the other fundamental forces (electromagnetism, the weak nuclear force, and the strong nuclear force), gravity does not have a specific range beyond which its effects are negligible. The strength of the gravitational force between two masses decreases with distance, but it never completely disappears.
Gravity dominates at the largest mass and distance scales because its effects are proportional to the mass of the objects involved. As the masses of the objects that are attracted to each other increase (the masses of planets and stars, for example, are very large), the gravitational force between them increases. This relationship is also the reason you are not attracted to the cup of coffee next to you. The cup does exert a gravitational force on you as you exert on the cup, but the magnitude of the force is so small that it is insignificant.
3.3 Gravitational and Electric Forces
The gravitational force of a planet is proportional to the product of the two masses and inversely proportional to the square of the distance between them. The equation for this force is F=
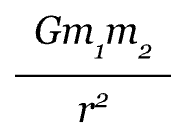
where F is the force of gravity, m1 and m2 are the masses of the two objects, r is the distance between the two objects and G is the gravitational constant. This equation is known as Newton's Universal Law of Gravitation, and it applies to every object in the universe -- even your physics notebook!
The gravitational force is always attractive and is responsible for the creation of galaxies, the general structure of the entire universe, and is the reason the Earth doesn't go hurtling off into space.
3.4 Gravitational Field/Acceleration Due to Gravity on Different Planets
On Earth, we know the gravitational acceleration to be 9.8 m/s/s. However, the gravitational acceleration on other planets is different, and in this topic, we learn how to find the value of the gravitational acceleration for any planet.
The equation
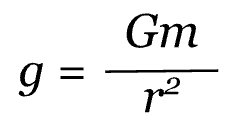
is a mathematical expression for the gravitational acceleration on a planet other than Earth, where G is the gravitational constant, M is the mass of the planet and R is the radius of the planet. It is also known as the "surface gravity" equation, and it describes the acceleration experienced by an object near the surface of a planet due to the planet's gravitational field.
The equation was derived by using Newton's Universal Law of Gravitation, which states that the force of gravity acting on an object is proportional to the product of the object's mass and the gravitational acceleration (g). The equation tells us that the gravitational acceleration on a planet depends on the mass and the radius of the planet.
A gravitational field is a region around an object in which another object experiences a force due to gravity. The gravitational field strength, also known as "g-force" is the acceleration experienced by an object in the field. The strength of a gravitational field is represented by the gravitational acceleration g.
3.5 Inertial vs. Gravitational Mass
Inertial mass and gravitational mass are two different types of mass that are associated with an object. Inertial mass is a measure of an object's resistance to acceleration, while gravitational mass is a measure of an object's strength of interaction with a gravitational field.
A common example used to illustrate the difference between inertial mass and gravitational mass is that of a bowling ball and a feather falling on the Earth and in a vacuum. On the Earth, both the bowling ball weighs more than the feather, so it falls to the ground faster than the feather. However, if we were to drop them in a vacuum, the bowling ball would fall at the same rate as the feather, due to the lack of air resistance.
The value of an object's inertial mass and its gravitational mass is found to always be the same for both types of mass, since inertial and gravitational mass are two ways of measuring the mass of an object.
3.6 Centripetal Acceleration and Centripetal Force
Centripetal acceleration in uniform circular motion is the acceleration of an object moving in a circular path at a constant speed. It is directed towards the center of the circle, and is what keeps the object moving in a circular path. The equation for centripetal acceleration is:
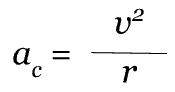
where a_c is the centripetal acceleration, v is the velocity of the object and r is the radius of the circle.
The velocity of an object in uniform circular motion is tangent to the acceleration. This means that the velocity vector is always at a 90-degree angle to the acceleration vector. This is because the direction of the velocity is constantly changing as the object moves in a circular path (the cause of the acceleration), but its magnitude is not, since the velocity remains constant. The velocity vector is pointing in the direction of motion (along the circle) at any given moment, and the acceleration vector is always pointing toward the center of the circle.
The centripetal force in uniform circular motion is the force that acts on an object moving in a circular path at a constant speed, and is responsible for keeping the object moving in a circular path. The centripetal force is not a new force; just another name for the net force in circular motion. This force could be tension, gravity, normal force, or friction. The equation for centripetal force using Newton's Second Law is:
F = ma = mv^2/r
where F is the centripetal force, m is the mass of the object, v is the velocity of the object and r is the radius of the circle.
3.7 Free-Body Diagrams for Objects in Uniform Circular Motion
A free body diagram (FBD) is a visual representation of the forces acting on an object. It is a powerful tool that can be used to analyze the motion of an object, such as an object undergoing uniform circular motion. You have already drawn countless free-body diagrams for projectile motion, but now it's time to apply the fundamentals you learned to uniform circular motion. When drawing a free body diagram for an object in uniform circular motion, it is important to select an appropriate coordinate system and to accurately represent the forces acting on the object.
Your positive x or y axis should be in the same direction as the centripetal acceleration. Since the centripetal acceleration vector always points toward the center of the circle, your positive axis should also be toward the center of the circle. If any of the forces acting on your object do not align with this coordinate system, you should break them into their x and y components.
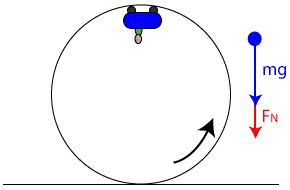
Image courtesy of APlusPhysics.
In this image, the car of a rollercoaster is at the top of a loop-the-loop. At the top, the weight of the car is a force vector pointing downwards. Since the normal force is caused by the force of the track on the car, the normal force is also pointing downwards, and both these forces will add to give us our net force, or centripetal force. Notice how the centripetal force is still pointing towards the center of the circle created by the loop-the-loop.
3.8 Applications of Circular Motion and Gravitation
An inertial frame of reference in physics is a reference frame in which an object is at rest or moving with a constant velocity. In an inertial frame of reference, the laws of physics are the same for all observers and all directions. In other words, if an experiment is performed in an inertial frame of reference, the results will be the same regardless of the velocity of the observer or the direction of the experiment.
For example, an observer who is standing in front of a ferris wheel might say the ferris wheel is rotating clockwise. However, a person standing behind the same ferris wheel will say the wheel is rotating counterclockwise.
The linear quantities used to represent position (x), velocity (v), and acceleration (a) all have rotational equivalents. The rotational analog for position is the angle θ (the Greek lowercase theta) in radians. The rotational analog for velocity is angular velocity, the change in angle divided by the change in time, measured in radians per second and represented by ω (the Greek lowercase omega). The rotational analog for acceleration is angular acceleration α (the Greek lowercase alpha), and it measures the change in angular velocity over time in radians per second squared.
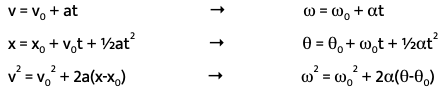
The kinematics equations can also be converted into rotational kinematics equations. Just like the kinematics equations only work in situations where there is a constant linear acceleration, the rotational kinematics equations only work in situations where there is a constant angular acceleration.
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
3.0Unit 3 Overview: Circular Motion and Gravitation
- Applicable Big Ideas
- 3.1 Vector Fields
- 3.2 Fundamental Forces
- 3.3 Gravitational and Electric Forces
- 3.4 Gravitational Field/Acceleration Due to Gravity on Different Planets
- 3.5 Inertial vs. Gravitational Mass
- 3.6 Centripetal Acceleration and Centripetal Force
- 3.7 Free-Body Diagrams for Objects in Uniform Circular Motion
- 3.8 Applications of Circular Motion and Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
📚Study Tools
🧐Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.