Daniella Garcia-Loos
Peter Apps
AP Physics 1 🎡
257 resourcesSee Units
Unit 4 introduces the concept of energy as an alternative method of solving some of the problems encountered in Units 1-3. The skills learned in this unit will become essential tools in dealing with some of the more advanced concepts in the later units. These topics will account for up to a quarter (~16-24%) of the AP exam questions and will take approximately 19-22 45 minute class periods to cover. This is a foundational unit to the course, and it’s vital you can understand and apply the concepts.
Applicable Big Ideas
- Big Idea #3: Force Interactions - How does pushing something give it energy?
- Big Idea #4: Change - How is energy exchanged and transformed within or between systems? How does the choice of system influence how energy is stored or how work is done?
- Big Idea #5: Conservation - How is energy transferred between objects or systems? How does the law of conservation of energy govern the interactions between objects and systems?

Image courtesy of Giphy.
Key Concepts 🔑
- Systems
- Work (W)
- Power (P)
- Gravitational Potential Energy (Ug)
- Elastic Potential Energy (Usp)
- Kinetic Energy (K)
- Conservation of Energy
Key Equations 🗝
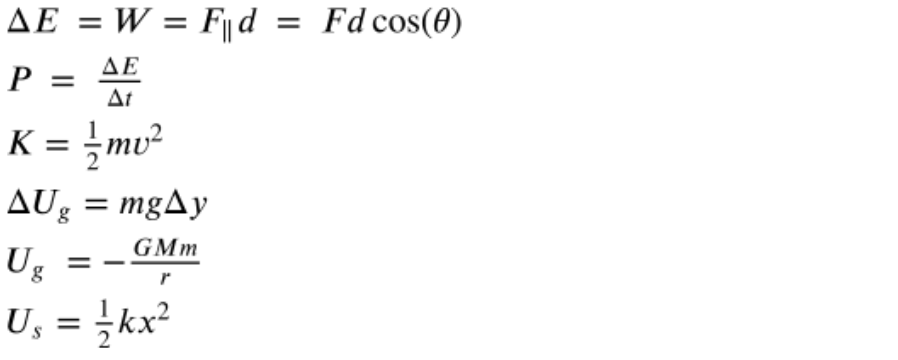
4.1 Open and Closed Systems: Energy
An open system is a system where matter and energy can be exchanged with its surroundings. An example of an open system in everyday life is a pot of water on a stove, where heat energy is transferred from the stove to the water, causing the water to boil.
A closed system, on the other hand, is a system where matter cannot be exchanged with its surroundings, but energy can be. An example of a closed system in everyday life is a sealed soda can, where the can prevents the exchange of matter (air) with the surroundings, but heat energy can be transferred to or from the soda, causing the temperature to change.
In terms of conservation of energy, this means that in an open system, energy can be transferred in or out of the system, but the total energy of the system plus its surroundings remains constant. In a closed system, the total energy of the system remains constant as long as no energy is transferred to or from the surroundings.
4.2 Work and Mechanical Energy
Work is defined as the force applied to an object multiplied by the distance over which the force is applied. Mathematically, work is represented by the equation W = Fd, where W is the work done, F is the force applied, and d is the distance over which the force is applied. Work is a scalar quantity and is measured in units of joules (J).
Energy is the ability to do work. Energy can take many forms, such as kinetic energy (the energy an object has due to its motion), potential energy (the energy an object has due to its position or configuration), and thermal energy (the energy an object has due to its temperature). The total energy of an object is the sum of all the different forms of energy it possesses.
In physics, it is important to understand that work and energy are related and can be converted from one form to another, for example, work can be used to increase the kinetic energy of an object, or the potential energy of an object can be converted into kinetic energy as it falls under the influence of gravity.
Mechanical energy is the sum of the kinetic energy and potential energy of an object in a mechanical system.
Kinetic energy is the energy an object possesses due to its motion. It can be calculated using the equation KE = (1/2)mv^2, where KE is the kinetic energy, m is the mass of the object, and v is the velocity of the object.
Potential energy is the energy an object possesses due to its position or configuration. There are various types of potential energy, but the most common are: gravitational potential energy and elastic potential energy. Gravitational potential energy is the energy an object possesses due to its height above a reference point, it can be calculated using the equation PE = mgh, where PE is the potential energy, m is the mass of the object, g is the acceleration due to gravity, and h is the height of the object above the reference point. Elastic potential energy is the energy stored in an object due to its deformation and can be calculated using the equation PE = (1/2)kx^2 where PE is the potential energy, k is the spring constant and x is the displacement from the equilibrium position.
The total mechanical energy of an object is the sum of its kinetic and potential energy. Mechanical energy is a scalar quantity and is measured in units of joules (J).
The law of conservation of mechanical energy states that the total mechanical energy of a closed system is constant as long as there is no work done by non-conservative forces such as friction. This means that if an object starts with a certain amount of mechanical energy, and no non-conservative forces are acting on it, the object will always have that same amount of mechanical energy.
4.3 Conservation of Energy, the Work-Energy Principle, and Power
The work-energy principle states that the work done on an object is equal to the change in its kinetic energy. Mathematically, it can be represented as W = ΔK, where W is the work done on the object, and ΔK is the change in the object's kinetic energy.
Power is a measure of the rate at which work is done or energy is transferred. It can be represented mathematically as P = W/t, where P is power, W is work done, and t is the time over which the work is done. Power is measured in units of watts (W).
Power can also be calculated as the rate of change of kinetic energy, by using the equation P = ΔK/t, where P is power, ΔK is the change in kinetic energy, and t is the time over which the change in kinetic energy occurs.
The work-energy principle and the concept of power are important in understanding many physical phenomena, such as the motion of objects under the influence of forces, the functioning of machines and engines, and the transfer of energy in various forms. For example, in a car engine, the work done by the combustion of fuel is converted into kinetic energy, which is then used to power the car's motion. The power of the engine can be measured by the rate at which work is done, or by the rate of change of kinetic energy of the car.
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
📚Study Tools
🧐Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.