📚

All Subjects

🎡

AP Physics 1

🎸

Unit 6

MC Answers and Review

9 min read•december 20, 2021

AP Physics 1 🎡

257 resources

See Units

Answers and Review for Multiple Choice Practice on Simple Harmonic Motion

Image courtesy of Pixabay

⛔STOP ⛔ Before you look at the answers make sure you gave this practice quiz a try so you can assess your understanding of the concepts covered in Unit 6. Click here for the practice questions: AP Physics 1 Unit 6 Multiple Choice Questions. Facts about the test: The AP Physics 1 exam has 50 multiple choice questions (45 single-select and 5 multiple-select) and you will be given 90 minutes to complete the section. That means it should take you around 15 minutes to complete 8 questions.

The following questions were not written by College Board and, although they cover information outlined in the AP Physics 1 Course and Exam Description, the formatting on the exam may be different.

1. The period of a pendulum depends upon

A. the length of the pendulum (from pivot to the bob's center)

B. the mass of the bob

C. the weight of the bob

D. the amount which the bob is displaced form its equilibrium position

Explanation: The period of a pendulum is based on the equation T = 2pi(sqrt)(L/g). Therefore, only the length and the value for gravity will affect the period.

📄 Study Unit 6.1: Period of Simple Harmonic Oscillators

2. A mass is tied to the end of a light string. The other end of the light string is tied to a fixed point on the ceiling to create a simple pendulum. The mass (known as the bob) is pulled back and released. Once released, the bob swings to and fro. Positions A, B, C, D and E represent various locations of the bob during the course of a back-and-forth cycle. Positions A and E are locations of the bob at its two extremes. At which location is the net force experienced by the bob the greatest?

A. A

B. B

C. C

D. D or E

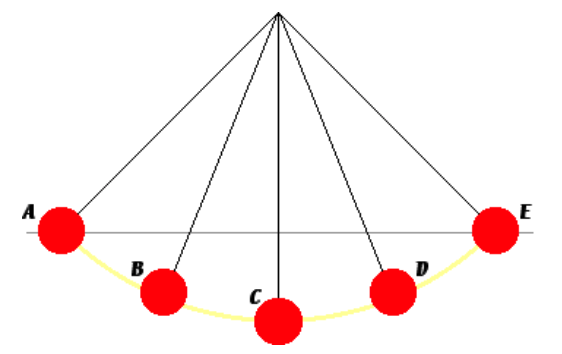
Explanation: The force of an object traveling in a circle is proportional to the mass times the centripetal acceleration of the object. Since the centripetal acceleration is = v^2/r, the position "C" has the highest velocity, the highest acceleration, and therefore the highest force.

📄 Study Unit 6.0: Simple Harmonic Motion

3. A mass is tied to the end of a light string. The other end of the light string is tied to a fixed point on the ceiling to create a simple pendulum. The mass (known as the bob) is pulled back and released. Once released, the bob swings to and fro. Positions A, B, C, D and E represent various locations of the bob during the course of a back-and-forth cycle. Positions A and E are locations of the bob at its two extremes. At which location(s) is/are the gravitational potential energy experienced by the bob the greatest?

A. A

B. C

C. E

D. A and E

Explanation: The highest position of the pendulum during the swing is the location of the maximum gravitational potential energy. Since it is at the highest position at A and E it is at those positions it has the most gravitational potential energy.

📄 Study Unit 6.0: Simple Harmonic Motion

4. The picture at the top of the diagram is of a pendulum exhibiting simple harmonic motion. The diagrams at the bottom have vector arrows. Which arrow represents the direction of the net force on the bob at location D?

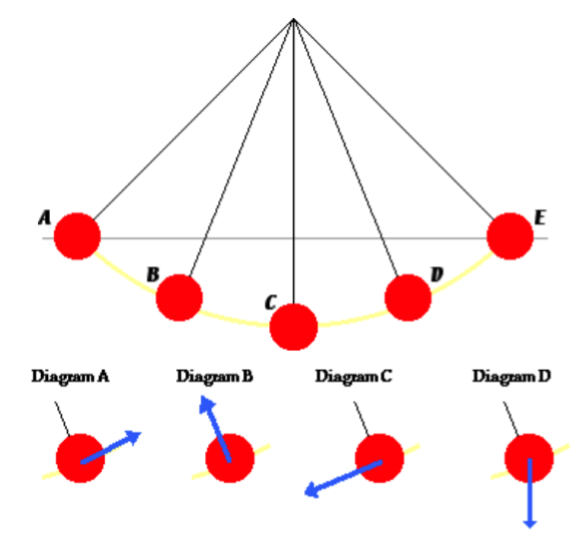
Explanation: The net force is the centripetal or "center seeking" force for an object traveling in a circle. Therefore, the only correct answer is "B"!

📄 Study Unit 6.0: Simple Harmonic Motion

5. The picture at the top of the diagram is of a pendulum exhibiting simple harmonic motion. The diagrams at the bottom have vector arrows. Which arrow represents the direction of the velocity on the bob when at location D traveling towards E?

Explanation: For an object traveling in a circle, the velocity (translational) is directed along a tangent line to the circle. Although "A" could be a tangential velocity, notice the question specifically states from D towards E.

📄 Study Unit 6.0: Simple Harmonic Motion

6. A mass is attached to a spring and allowed to hang vertically from a fixed support. The spring naturally stretches to position A. The mass is then pulled down to position B and released. The mass then vibrates up and down in periodic fashion. Positions C to G represent random positions of the mass over the course of several cycles of up and down motion. A background grid is shown in the graphic. Each small square on the grid measures 4 cm along its edge. At which listed position is the net force acting upon the mass equal to 0 N?

A. C

B. D

C. E

D. F

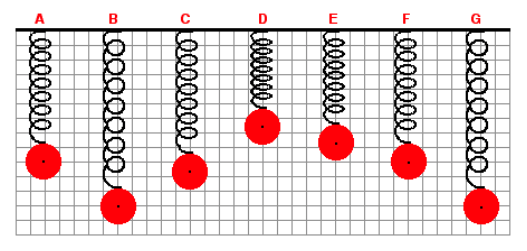
Explanation: The equilibrium point, A, is where the forces are balanced (Fs up and Fg down). Since "F" is at the same position, it is also a point where the net force is 0 N.

📄 Study Unit 6.1: Period of Simple Harmonic Oscillators

7. A mass is attached to a spring and allowed to hang vertically from a fixed support. The spring naturally stretches to position A. The mass is then pulled down to position B and released. The mass then vibrates up and down in periodic fashion. Positions C to G represent random positions of the mass over the course of several cycles of up and down motion. A background grid is shown in the graphic. Each small square on the grid measures 4 cm along its edge. The spring force exerted upon the mass is maximum when the mass is at position

A. D

B. E

C. F

D. G

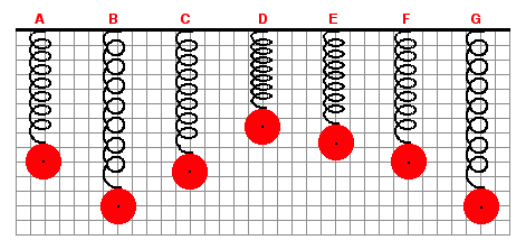
Explanation: The spring force, Fs = kx, so just look for where the spring is stretched

📄 Study Unit 6.0: Simple Harmonic Motion

8. A mass is attached to a spring and allowed to hang vertically from a fixed support. The spring naturally stretches to position A. The mass is then pulled down to position B and released. The mass then vibrates up and down in periodic fashion. Positions C to G represent random positions of the mass over the course of several cycles of up and down motion. A background grid is shown in the graphic. Each small square on the grid measures 4 cm along its edge. Determine the amplitude of the mass while it is in SHM.

A. 3 cm

B. 12 cm

C. 24 cm

D. 48 cm

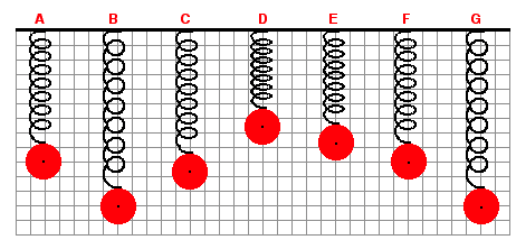
Explanation: The amplitude is just the distance from the equilibrium point (A) to the furthest stretch/compression (B). 3 boxes x 4cm/box = 12 cm.

📄 Study Unit 6.1: Period of Simple Harmonic Oscillators

9. A body of mass 5.0 kg is suspended by a spring that stretches 10 cm when the mass is attached. It is then displaced downward an additional 5.0 cm and released. Its position as a function of time is approximately

A. y = .05cos9.9t

B. y=.10sin9.9t

C. y=.10cos9.9t

D. y=.10cos(9.9t+5)

Explanation: From the AP Physics 1 equation sheet, x=Acos(2pift). Since A is the amplitude, and you set the spring into motion by pulling it down 5 cm, the only answer with A = .05m is the correct answer.

📄 Study Unit 6.1: Period of Simple Harmonic Oscillators

10. "A mass m = 2.0 kg is attached to a spring having a force constant k = 290 N/m as in the figure. The mass is displaced from its equilibrium position and released. Its frequency of oscillation (in Hz) is approximately "

A. 0.01

B. 0.5

C. 1.9

D. 12

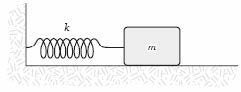
Explanation: Ts=2pi*sqrt(m/k). Therefore, Ts=2pi*sqrt(2/290) = .526 s. Also, f = 1/Ts = 1/.526 = 1.9 Hz.

🎥 Watch: Problem-Solving/Q&A: Simple Harmonic Oscillators

11. A weight of mass m is at rest at O when suspended from a spring, as shown. When it is pulled down and

released, it oscillates between positions A and B. Which statement about the system consisting of the spring

and the mass is correct?

A. The gravitational potential energy of the system is greatest at A.

B. The rate of change of momentum has its greatest magnitude at A and B.

C. The elastic potential energy of the system is greatest at O.

D. The rate of change of gravitational potential energy is smallest at O.

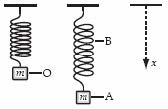
Explanation: The kinetic energy is the greatest when the oscillating spring is at equilibrium. Therefore, the speed is also the greatest at that point. Since momentum = mass*velocity, the maximum momentum is also at that same point.

🎥 Watch: Problem-Solving/Q&A: Simple Harmonic Oscillators

12. A block attached to an ideal spring undergoes simple harmonic motion. The acceleration of the block has its maximum magnitude at the point where

A. The speed is a minimum

B. The speed is a maximum

C. The restoring force is the minimum

D. the kinetic energy is the maximum

Explanation: The acceleration of the block has its maximum magnitude at the points where its displacement from equilibrium has the maximum magnitude (since a = F/m = kx/m). At the endpoints of the oscillation region, the potential energy is maximized and the kinetic energy (and hence the speed) is zero.

🎥 Watch: Problem-Solving/Q&A: Simple Harmonic Oscillators

13. A block with a mass of 20 kg is attached to a spring with a force constant k = 50 N/m. What is the magnitude of the acceleration of the block when the spring is stretched 4 m from its equilibrium position?

A. 4 m/s^2

B. 6 m/s^2

C. 8 m/s^2

D. 10 m/s^2

Explanation: Using a=kx/m = 50*4/20 = 10 m/s^2

📄 Study Unit 6.0: Simple Harmonic Motion

14. A block with a mass of 10 kg connected to a spring oscillates back and forth with an amplitude of 2 m. What is the approximate period of the block if it has a speed of 4 m/s when it passes through its equilibrium point?

A. 1s

B. 3s

C. 6s

D. 12s

Explanation: By Conservation of Mechanical Energy, the energy of the block is the same throughout the motion. At the amplitude, the block has potential energy Us=1/2kx^2 and zero kinetic energy. At the equilibrium position, the block has kinetic energy K=1/2mv^2 and zero potential energy. Applying the Conservation of Mechanical Energy to these two points in the motion yields k = 40 kg/s (or 40 N/m).

The period of the block can then be calculated using the following equation: T=2pi(sqrt)(m/k) = 2pi(sqrt)(10/40) = 3 s.

📄 Study Unit 6.1: Period of Simple Harmonic Oscillators

15. A block with a mass of 4 kg is attached to a spring on the wall that oscillates back and forth with a frequency of 4 Hz and an amplitude of 3 m. What would the frequency be if the block were replaced by one with one-fourth the mass and the amplitude of the block is increased to 9 m ?

A. 4 Hz

B. 8 Hz

C. 12 Hz

D. 24 Hz

Explanation: The frequency of a spring-block simple harmonic oscillator is independent of the amplitude. The equation for the frequency of a spring-block simple harmonic oscillator is f = 1/2pi*sqrt(k/m). The frequency is inversely proportional to the square root of the mass, so decreasing the mass of the block by a factor of 4 would increase the frequency by a factor of 2.

🎥 Watch: Problem-Solving/Q&A: Simple Harmonic Oscillators

What can we help you do now?