Briana Dokken
AP Physics 1 🎡
257 resourcesSee Units
As of 2021, College Board only tests Units 1-7 on the AP Physics 1 exam. This page's content will not be tested on the exam, but we kept it online for you all as a resource.
Measuring Charge and Electric Force
What is Charge? 🔆
Charge is a property of matter, just like mass, physical state, or density. When an atom has the same number of protons (positively charged particles) and electrons (negatively charged particles), the positive and negative charges of the atom cancel out, and its net charge is 0; we refer to the atom as uncharged when this occurs. However, when electrons are taken away or added to an atom, it becomes charged. Charge depends entirely on the movement of electrons.

Image Courtesy of Vox.com
How Do Things Become Charged? 🚗
There are two kinds of charge: positive charge and negative charge. Electrons have a negative charge, so an atom becomes negatively charged when it has additional electrons. When you take away electrons from an atom, it becomes positively charged because the substance's protons outnumber the number of electrons. Like with magnets, opposite forces attract and like forces repel when discussing protons and electrons. Therefore:
- Positive and negative charges attract one another
- Similar charges (positive and positive, negative and negative) repel each other.
The arrangement of electrons can also influence charge. A substance can have a partial charge and repel or attract other charged objects, even if there is no change in electron count, like in the case of dipoles. For example, if a substance's electrons move to one side, that occupied half will have a partial negative charge, and the other side will have a partial positive charge. Physicists refer to this separation of positive and negative charges as a dipole.

Measuring Charge 🎛
Charge is measured in coulombs (C). Since atoms become charged when electrons are added or removed, the charge of an atom is always a whole number multiple of an electron's charge. For example, if we take 3 electrons from an atom, its charge is now three times the charge of one electron. Similarly, if we gave an atom three additional electrons, its charge would be negative three times that of one electron. (For reference, the charge of an electron, also known as the elementary charge, is 1.602 x 10-19 C.)
Often, we call charged particles "charges" or "point charges" if we assume that the charge focuses at a single point. If you see the word "charge" from here on out, know that it means a charged particle.

GIF courtesy of gyfcat.com
Electric Force 🔋
When two charges are near each other, each charge exerts the same force on the other. This force is either attractive or repulsive (remember, opposites attract and like forces repel). If two positive or negative charges are near each other, each charged particle exerts a repulsive force on the other; likewise, if a positively charged particle and a negatively charged particle are near each other, each exerts an attractive force on the other. We can quantify this force using Coulomb's law:

Notice that as the distance between the two charges increases (r2), the force decreases, meaning they are inversely proportional. As either of the charges increases, electric force increases, so electric force and charge are directly proportional. This equation also includes Coulomb's constant k, which stays the same every time you use the formula. Sometimes, it is referred to as a proportionality constant.
Coulomb’s Law Example 🔌
Let's go over an example of how we can use Coulomb's Law to find how much force one charge exerts on another. Assume we have two atoms: Atom 1 has one additional electron added, and Atom 2 is missing 1 electron. Both of these two atoms are 0.5 m away from one another. What is the electric force on one of the charges?
The first step to solving this problem is to plug each given variable into Coulomb's Law. After inserting values and solving for Fe, we should get:

In the end, each of these particles experiences an attractive force of 9.23 10-28 N on it. From this value, we know the force acting on Atom 1 points to the right towards Atom 2, and the force on Atom 2 points to the left towards Atom 1. If these two atoms had the same charge, Atom 1 would experience a force to the left, and Atom 2 would experience a rightward force since like charges repel.
Superposition Principle ➕
Like with other forces, when multiple electric forces act on one charge, we can add up those forces to find the net force on the charge. We treat forces as vectors and add up force like vectors.
In this example, let’s assume that Atoms 1 and 2 have a positive charge and Atom 3 has a negative charge. To find the net force on Atom 1, we would add up the forces from Atoms 2 and 3 to get a net force pointing towards the right, greater than each F2 and F3 individually. Atom 2 repulses Atom 1 to the right, and Atom 3 attracts 1 to the right, so we should have a net force pointing to the right equal to the sum of F2 and F3.
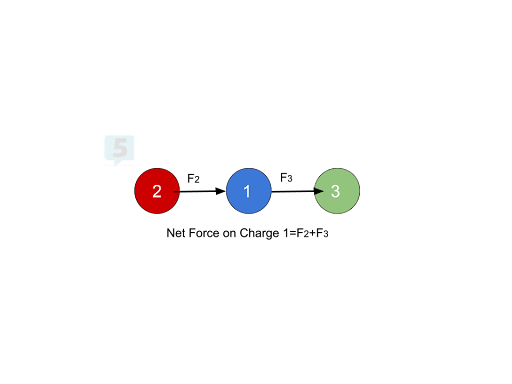
Net Forces at an Angle 💡
If a force acts on a charge at an angle, we can split it into an x and y component and then solve for the net force in the x-direction and y-direction. However, there are some limitations to this process. If we know the angle at which the force is acting and the overall electric force, we can easily find the x and y-components of the electric force. If we only know the x and y components of the electric force, though, we can solve for the overall electric force.
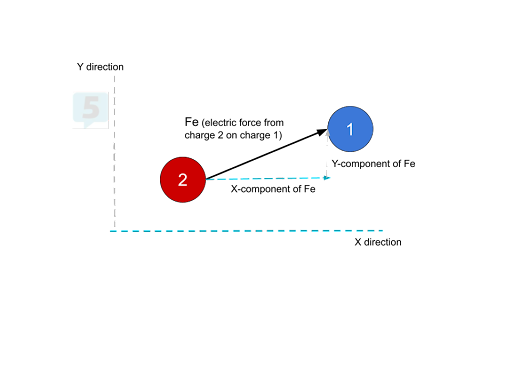
Suppose multiple electric forces are acting on a charge pointing in numerous directions. In that case, we can add up all of the x component forces to find the net force in the x-direction and add up all the y-component forces to find the net force in the y-direction. Then, we can use the Pythagorean theorem and some trigonometry to find the total net force and its direction.
Practice Problems! ❔
Use Coulomb's law and your knowledge of splitting apart and adding together components of forces to solve these practice problems! You'll need the following values to solve these questions:
charge of an electron = 1.602 x 10^(-19) C
and
k = 8.99 x 10^(9) Nm^(2)/C^(2)
- 4.16*10^(19) electrons are moved through a wire. How many Coulombs of charge were moved?
- How strong is the attractive force between a sock with -2.00C of charge and a square of carpet with 3.00C of charge? The sock and carpet are 0.500m apart, and we can assume they act like point charges.
- Find the net force on q3. q1=-2.00*10^(-3)C, q2=-1.00*10^(-3)C, q3=+3.00*10^(-3)C. q1 is at (0,-3), q2 is at (3,0), and q3 is at (0,2).
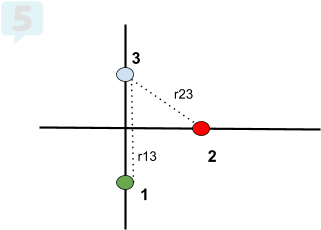



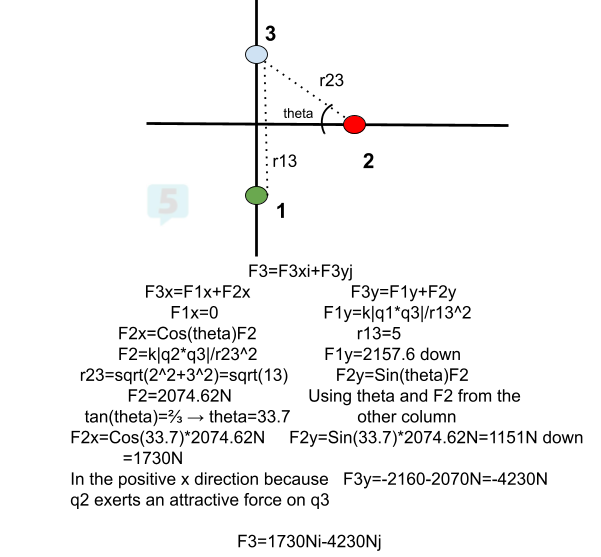
What to Know about Electric Force 👀
Overall, electric force is very similar to other forces you have learned about so far. Objects that are charged (have gained or lost electrons) exert a force on each other, which we call the electric force. Just like with all other forces, electric force is a vector. The net electric force acting on a charge can be found by adding up the x and y components of each electric force acting on a charge. We find electric force by using Coloumb’s Law, which says Fe=k|q1q2|/r^2.
Browse Study Guides By Unit
👟Unit 1 – Kinematics
🌀Unit 2 – Dynamics
🚀Unit 3 – Circular Motion & Gravitation
⚡️Unit 4 – Energy
⛳️Unit 5 – Momentum
🎸Unit 6 – Simple Harmonic Motion
🎡Unit 7 – Torque & Rotational Motion
💡Unit 8 – Electric Charges & Electric Force
🔋Unit 9 – DC Circuits
🔊Unit 10 – Mechanical Waves & Sound
📚Study Tools
🧐Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.