K
Krish Gupta
Daniella Garcia-Loos
AP Physics 2 🧲
61 resourcesSee Units
Vector and Scalar Fields
Vector and scalar fields are a Calculus 3 topic. But, they are easy enough and important enough that we learn to look at and read basic vector and scalar graphs.
Before we get into the actual fields, let's review scalar vs. vectors!
Scalar vs. Vector 💫
Scalar—quantities that are described by magnitude (a numerical value) alone.
Example: She is five feet tall
- Distance and Speed are scalar quantities
Vector—quantities that are described by a size (magnitude) and a direction (ex. East, Up, Right, etc)
Example: The gas station is five miles west from the car
- Displacement, Velocity, and Acceleration are vector quantities
Vectors can also be represented by arrows, and the length of the arrow should represent the magnitude of the described quantity.
Here are some key points about vectors and scalars:
- A vector is a quantity that has both magnitude and direction. Examples of vectors include velocity, force, and displacement.
- A scalar is a quantity that has only magnitude. Examples of scalars include mass, temperature, and energy.
- Vectors can be added and subtracted using vector addition and subtraction, which involves both the magnitude and direction of the vectors. Scalars can be added and subtracted using simple arithmetic.
- Vectors can be multiplied by scalars using scalar multiplication, which changes the magnitude of the vector but not its direction.
- Vectors can be represented graphically using arrow diagrams, with the length of the arrow representing the magnitude of the vector and the direction of the arrow representing the direction of the vector. Scalars are usually represented as single numbers.
Vector Fields Snapshot
Properties: Magnitude and Direction
Representation: Arrows (curves)
Quantity Commonly Used to Graph: Electric Field
Direction: Represented by the arrow
Magnitude: Represented by the density of the curves and arrows
Here are some key points about vector fields:
- A vector field is a mathematical representation of a vector-valued function in space.
- A vector field assigns a vector to each point in space, which means it can be used to represent things like the force field around a magnet or the flow of a fluid.
- The vectors in a vector field can be plotted as arrows on a graph, with the direction and length of the arrow representing the direction and magnitude of the vector at that point.
- Vector fields can be used to visualize and understand how quantities change over a given area or region. For example, a vector field could be used to show how the wind velocity changes as you move across a region, or how the temperature changes as you move through a room.
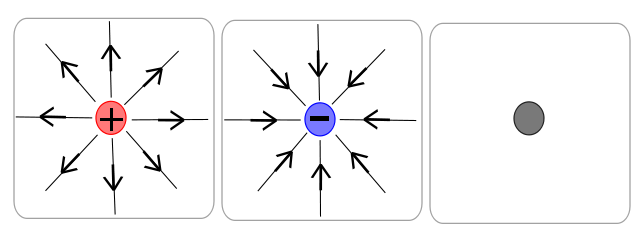
Image from wikimedia.org
- Two Point Charges
Image from Ck12.org
Scalar Fields Snapshot
Properties: Magnitude
Representation: Curves
Quantity Commonly Used to Graph: Electric Potential
Direction: None
Magnitude: Written on the curves or a key given to the side
Here are some key points about scalar fields:
- A scalar field is a function that assigns a scalar value (a single number) to every point in space.
- Scalar fields can be used to represent things like temperature, pressure, and density.
- Scalar fields are often visualized using contour maps, which show lines of equal value. For example, a temperature scalar field might be represented using a contour map with lines showing areas of equal temperature.
- Scalar fields can be used to understand and analyze how a particular quantity changes over a given area or region. For example, a scalar field could be used to show how the temperature changes as you move through a room, or how the density of a fluid changes as you move through it.
- Scalar fields are often used in physics, engineering, and other fields to model and analyze physical phenomena.
- Scalar fields can be combined with vector fields to create more complex models of physical systems. For example, a temperature scalar field could be combined with a velocity vector field to model the flow of a fluid.
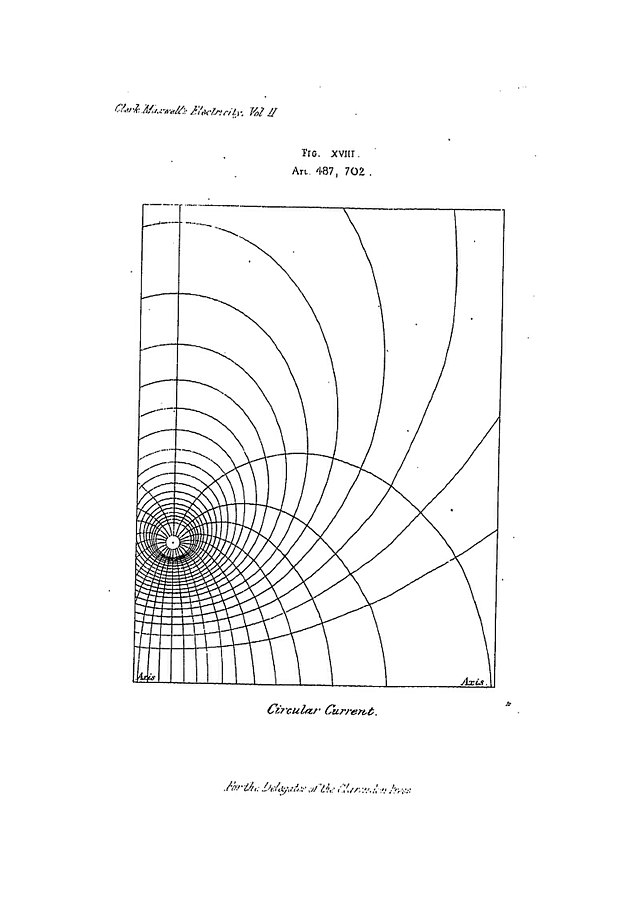
Borrowed from Wikimedia
Browse Study Guides By Unit
💧Unit 1 – Fluids
🔥Unit 2 – Thermodynamics
⚡️Unit 3 – Electric Force, Field, & Potential
💡Unit 4 – Electric Circuits
🧲Unit 5 – Magnetism & Electromagnetic Induction
🔍Unit 6 – Geometric & Physical Optics
⚛️Unit 7 – Quantum, Atomic, & Nuclear Physics
📆Big Reviews: Finals & Exam Prep
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.