2.3 Newton's Laws of Motion: Third Law
6 min read•january 18, 2023
Gerardo Rafael Bote
Daniella Garcia-Loos
AP Physics C: Mechanics ⚙️
68 resourcesSee Units
Newton's Laws of Motion: Third Law
Newton's Third Law is one of the most quoted lines in physics, yet sometimes it feels like the most abstract of the three laws.
Newton's Third Law of Motion: For every action, there is an equal and opposite reaction.
Key things to remember about Newton's Third Law:
- This means that if one object exerts a force on a second object, the second object will exert an equal and opposite force on the first object.
- The forces are always of the same magnitude but act in opposite directions.
- The law applies to all types of forces, including gravitational, electromagnetic, and strong and weak nuclear forces.
- The law is also often referred to as the "action-reaction law" or the "law of equal and opposite reactions."
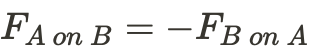

Image from Wikimedia Commons
What you should take away from this law is that force pairs exist in systems.
Force Pairs are always:
- Inside the system of the two objects that are interacting
- The same type of force (Ex: Tension)
- Equal magnitudes, opposite directions
If you struggle to recognize force pairs, try to circle them together or make them the same color when you draw your free-body diagrams! Additionally, you should be prepared for many systems of equations!
- To determine force pairs, you need to identify the two objects that are interacting and the direction of the force that each object is exerting on the other.
- The action and reaction forces are always equal in magnitude but opposite in direction.
- The force exerted by the first object on the second is considered the action force, and the force exerted by the second object on the first is considered the reaction force.
Some common force pairs include:
- The force of friction between two surfaces in contact
- The force of tension in a rope or cable
- The force of air resistance against an object moving through the air
- The force of gravity acting on two objects
- The force of magnetism between two magnets
Atwood Machines
Atwood machines are seen all the time in physics problems (AP loves them!), and they are a prime example of Newton's Third Law!
Here are some key things to know about Atwood Machines:
- An Atwood machine is a simple device used to demonstrate Newton's second law of motion, which states that the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.
- It consists of two masses, m1 and m2, connected by a string that runs over a pulley.
- The masses can be moved up and down by applying a force to one or both of them.
- The acceleration of the system can be calculated by measuring the change in velocity over time and dividing it by the net force acting on the system.
- The Atwood machine can be used to demonstrate a variety of physics concepts, such as the relationship between force, mass, and acceleration, the concept of tension in a rope or cable, and the conservation of mechanical energy.
- It is also used to demonstrate how the acceleration of an object is affected by the forces acting on it and how the acceleration of the system is dependent on the mass of the objects.
- The Atwood machine is a simple mechanical system and can be constructed using basic materials like pulley, rope, and masses.
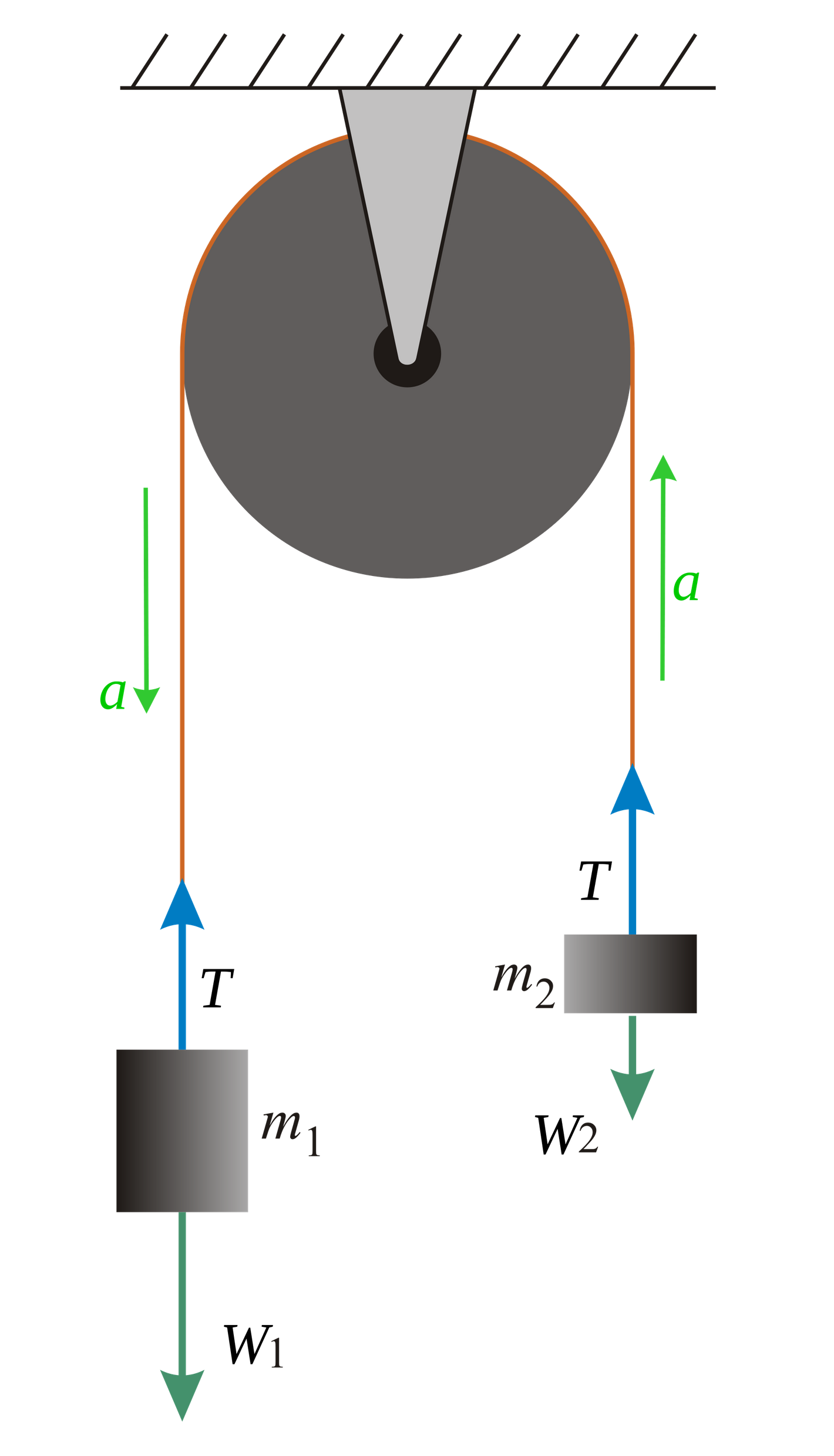
Image from Wikimedia Commons
By combining Newton's second and third law, you can derive some formulas to describe this scenario. First, you can usually assume the string is weightless and frictionless and that the pulley has no moment of inertia (you'll learn about this in a future unit!). This means that the only forces acting on the objects are tension and gravity.
Usually, in Atwood machine questions, you are asked to determine the acceleration of the system, so let's try to find it! For this specific instance of an Atwood machine, there are only forces in the Y direction, so let's isolate the forces acting on Mass 1 and Mass 2.
Start off by drawing Free Body Diagrams for Mass 1 and Mass 2 then writing the corresponding equations.

Now we can get rid of T (Tension) by combining these equations.
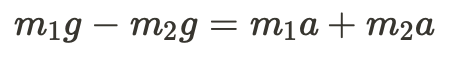
Factor out g and a:
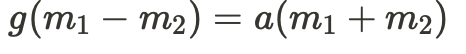
One final step to isolate a:

⚠️Is that it? It seems so easy... What can I get confused about with Newton's 3rd Law? TBH, a lot! There are many mistakes you can make with Newton's 3rd Law. You should take note of the following:
- "Forces occur only in pairs. Any force by one object on another cannot exist without the existence of an equal and opposite reaction force. A single force without a reaction counterpart does not exist in the world of physics." (Paul G. Hewitt)
- Gravity (i.e., gravitational force) is also considered with Newton's 3rd Law! As you push your weight down on Earth, the planet will also push you back up.
- Force pairs DO NOT cancel each other out. Instead, the action force and reaction force just apply themselves to different systems. For example, take a look at the picture below.
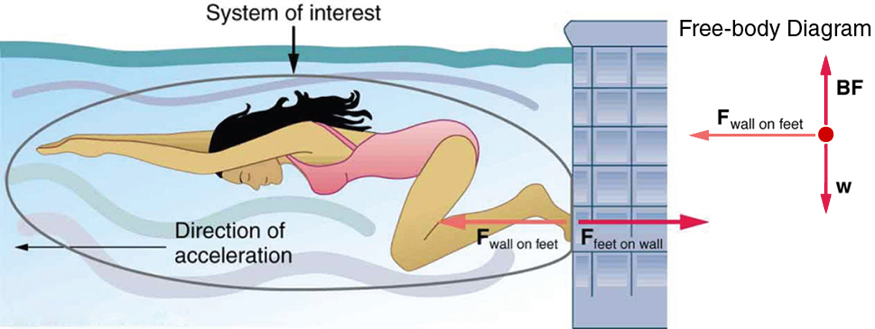
Image from OpenStax
You can probably identify that the action-reaction pair is the forces dealing with the swimmer's push on the wall. Based on the circled system, F_{wall space on feet} is considered in the swimmer's free body diagram, including her weight and the buoyancy force she experiences while swimming.
Practice Questions
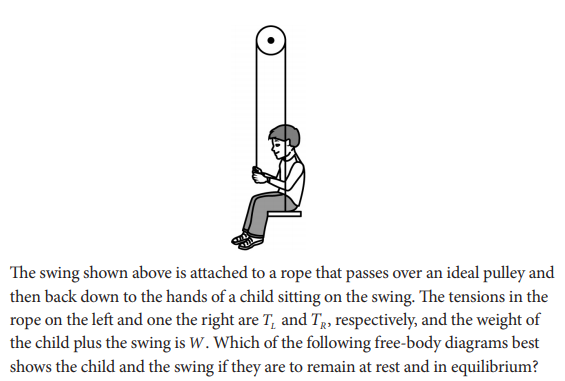
Image from collegeboard.org

Image from collegeboard.org
The correct answer is D. It was obvious that the weight vector (W) is pointing down, but now the question is: where do the tensions of each side of the rope point toward? Since we want "to remain at rest and in equilibrium," it should be concluded that Σ F =0 and that there is no acceleration taking place. Therefore, we should try to make the forces in the free body diagram relatively equal to each other (i.e, make sure that each dimension in the FBD cancels out). This instantly eliminates B & C as the vectors do not cancel each other out (i.e., there is a net force taking place). Finally, it doesn't make sense that either only T_L or T_R does not carry all the weight of the child on the swing. Besides, T_L allows the child to hold the rope to make himself in static equilibrium. This eliminates A & E. Since T_L and T_R are smaller than W and equal in size, the likely answer is D.
Answer
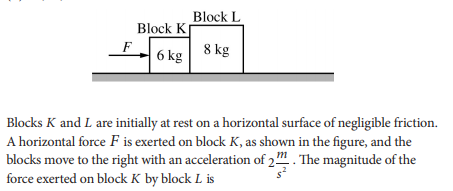
To complete this problem, you need to fully integrate Newton's 3rd Law into the relationships among the blocks. For me, I see the following relationships (i.e., net force equations for each block):
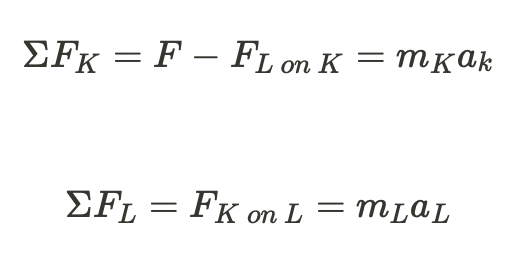
Since you know that both blocks are moving to the right with an acceleration of 2\space m/s^2, it can be declared that:

Knowing Newton's 3rd Law, you can also determine that:
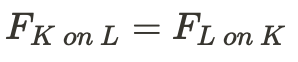
⚠️Wait, isn't there supposed to be a negative sign in the equation above? Yes, but that is only showing the relationship in action-reaction pairs that one force goes to the opposite way of the other force. Here, I'm showing that the action-reaction pairs are equal in magnitude.
Now you treat the following equations above by doing substitutions:

Lastly, you put 28 N in the first equation above to figure the magnitude of F_{L on K}:
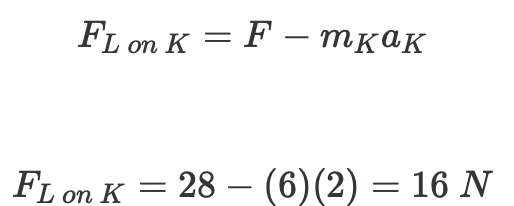
If you need more help, watch this YouTube video made by AbrahamPhysics

Image from Varsity Tutors
(Hint: Use g=9.81 m/s2g=9.81 m/s2)
Answer
Since Dave weighs 589 N, that must mean his mass is:

Since he accelerated at 4 \space m/s^2, we can determine that he was pushed off by the ground with:
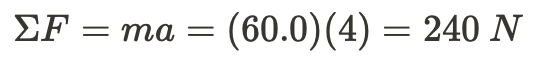
By Newton's 3rd law of motion, Dave must also have pushed of the ground with a force of 240 Newtons.
Browse Study Guides By Unit
🚗Unit 1 – Kinematics
🚀Unit 2 – Newton’s Laws of Motion
🎢Unit 3 – Work, Energy, & Power
🎳Unit 4 – Systems of Particles & Linear Momentum
🚲Unit 5 – Rotation
🌊Unit 6 – Oscillations
🪐Unit 7 – Gravitation
🙏Exam Reviews

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.