📚

All Subjects

⚙️

AP Physics C: Mech

🎢

Unit 3

3.1 Work-Energy Theorem

5 min read•january 13, 2023

Daniella Garcia-Loos

AP Physics C: Mechanics ⚙️

68 resources

See Units

Unit 3: Work, Energy, and Power

Overview

Energy is one of the biggest concepts in physics, and you can see it in every unit we've covered in the past and will cover in the future. A tip given to me by a wise physics teacher was that almost every FRQ can be at least partially tackled with energy!

Big Ideas

Force Interactions

Why is no work done when you push against a wall, but work is done when you coast down a hill

Conservation:

Why does a stretched rubber band return to its original length?
Why is it easier to walk up a flight of steps, rather than run, when the gravitational potential energy of the system is the same?

Force Interactions:

Why is no work done when you push against a wall, but work is done when you coast down a hill?

Exam Impact

Unit 3 will cover approximately 14%-17% of the exam and should take around 10 to 20, 45-minute class periods to cover. The AP Classroom personal progress check has 20 multiple choice questions and 1 free response question for you to practice on.

Work-Energy Theorem 💪

The net work done on a (point-like) object is equal to the object’s change in the kinetic energy.

The work-energy theorem is a fundamental principle in physics that relates the work done on an object to the change in its kinetic energy. Here are some key concepts and implications of the theorem:

Work is defined as the dot product of force and displacement. Mathematically, it can be represented as W = Fdcosθ, where F is the force, d is the displacement, and θ is the angle between the force and displacement vectors.
Kinetic energy is the energy an object possesses due to its motion. It is given by the formula KE = 1/2mv^2, where m is the mass of the object and v is its velocity.
The work-energy theorem states that the work done on an object is equal to the change in its kinetic energy. So if W is the work done on an object and ΔK is the change in its kinetic energy, then W = ΔK.
This means that any work done on an object will cause a change in its kinetic energy. For example, if you apply a force to an object and make it move, the work you do will increase the object's kinetic energy. Conversely, if you apply a force in the opposite direction to slow down an object, the work you do will decrease its kinetic energy.
The theorem applies to both conservative and non-conservative forces. Conservative forces are forces that depend only on the object's position, such as gravitational and spring forces. Non-conservative forces are forces that depend on the object's velocity, such as friction and air resistance. The work-energy theorem states that the work done by any force, whether conservative or non-conservative, will cause a change in the object's kinetic energy.
The theorem also applies to systems where multiple forces are acting on the object. For example, if you have an object being pushed by two different forces, the work done by the forces will be added together to determine the change in kinetic energy of the object.
The theorem can be used to calculate the work done by a force and the change in kinetic energy of an object. For example, if you know the force and displacement of an object, you can use the work-energy theorem to calculate the change in its kinetic energy. Or, if you know the initial and final kinetic energy of an object, you can use the theorem to calculate the work done on it.
The theorem is valid only for the case of constant mass. If the mass of an object changes, the theorem is no longer valid.

In equation form, the Work-Energy Theorem looks like this:

In which W is work and K is kinetic energy.

Kinetic energy is typically defined as:

where m is mass and v is velocity.

Here is the derivation of the Work-Energy Theorem:

F=dv/dt then use the chain rule

And we know that the equation for work is W = Fxd so:

W=m[1/2(v^2)] evaluated from Vo to Vf

Work done by a variable force is the area under a force vs radius plot! This can be seen in your formula chart as:

⚠️Wait...what is work?

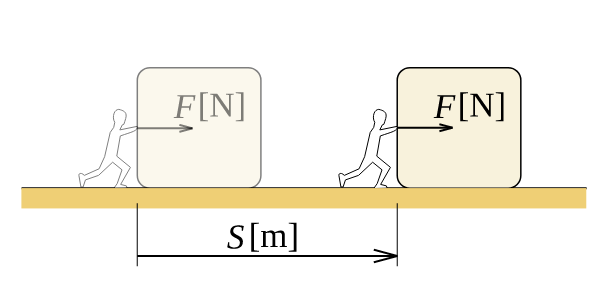
Image from Wikimedia Commons

Work is when there is a force exerted on an object that causes the object to be displaced. Work is a scalar that can be negative or positive, depending on if there's energy put in or taken out of the system.

If you know about vectors, you should be aware that work is the scalar product between force and displacement. Only the force parallel to the direction of motion is included.

Here's the most popular formula for work that is not calculus based:

Practice Questions:

1. (a) Calculate the work done on a 1500-kg elevator car by its cable to lift it 40.0 m at constant speed, assuming friction averages 100 N.

(b) What is the work done on the lift by the gravitational force in this process?

Answers:

(a) Start by drawing a free body diagram, with the force of tension and the gravitational force.

(b)

(c) The only two forces that are doing work on the lift are gravity and tension, not friction. Therefore the net amount of work is zero.

2. (a) Using energy considerations, calculate the average force a 60.0-kg sprinter exerts backward on the track to accelerate from 2.00 to 8.00 m/s in a distance of 25.0 m, if he encounters a headwind that exerts an average force of 30.0 N against him. (Taken from Lumen Learning)

Answer:

Always start by drawing your free body diagram!

Let's start off with a tried and true classic: Newton's Second Law