4.3 Conservation of Linear Momentum and Collisions
3 min read•june 18, 2024
Daniella Garcia-Loos
AP Physics C: Mechanics ⚙️
68 resourcesSee Units
Conservation of Linear Momentum in a System🎱
Conservation of Linear Momentum
The total momentum, magnitude, and direction are conserved in a system unless acted on by an outside force.
Here are some key things to remember about the conservation of linear momentum:
This law of conservation can also be written as:

The initial momentum is equal to the final momentum, if there was no impulse.
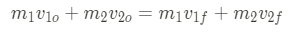
⚠️So...why is momentum conserved in a collision?
We have to blame it on Newton, again! Think back to Newton's Third Law: every action has an equal and opposite reaction. This means that there is an equal and opposite force acting on the two objects that collided.
So let's see if there's an impulse from a collision. Since impulse is equal to the change in momentum, if it is 0, we know that momentum was conserved. The change in momentum of both objects is the same magnitude, but different directions. So the sum of these is zero!
Collisions
A collision is the most basic application of conservation of momentum, from pool balls knocking each other to a rocket launching, collisions occur daily. They typically involve a system of masses interacting with some speed. The forces these masses enact on each other do not affect the conservation of momentum of the system, because there is no net force!
Below is an example of a scenario before and after, where momentum is conserved:
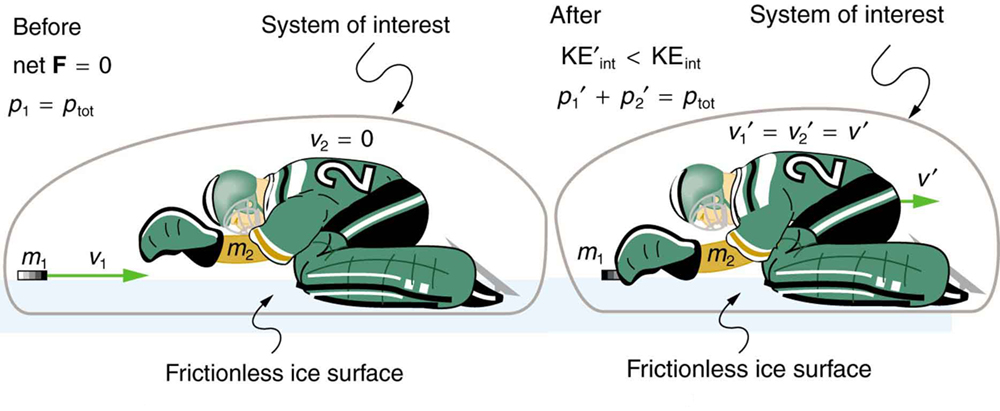
Taken from Lumen Learning
Elastic Collisions:
- Momentum is conserved
- Mechanical energy is conserved
- Kinetic energy is conserved
- Sometimes referred to as "Bouncy" collisions
Inelastic Collisions:
- Momentum is conserved
- Mechanical energy is conserved
- Kinetic energy is not conserved
- If a collision is perfectly inelastic or "sticky", the max amount of kinetic energy is lost
Here's a fun interactive cart lab you can mess around with! Check out the different types of collisions and how velocity and mass affect the system.
Practice Questions
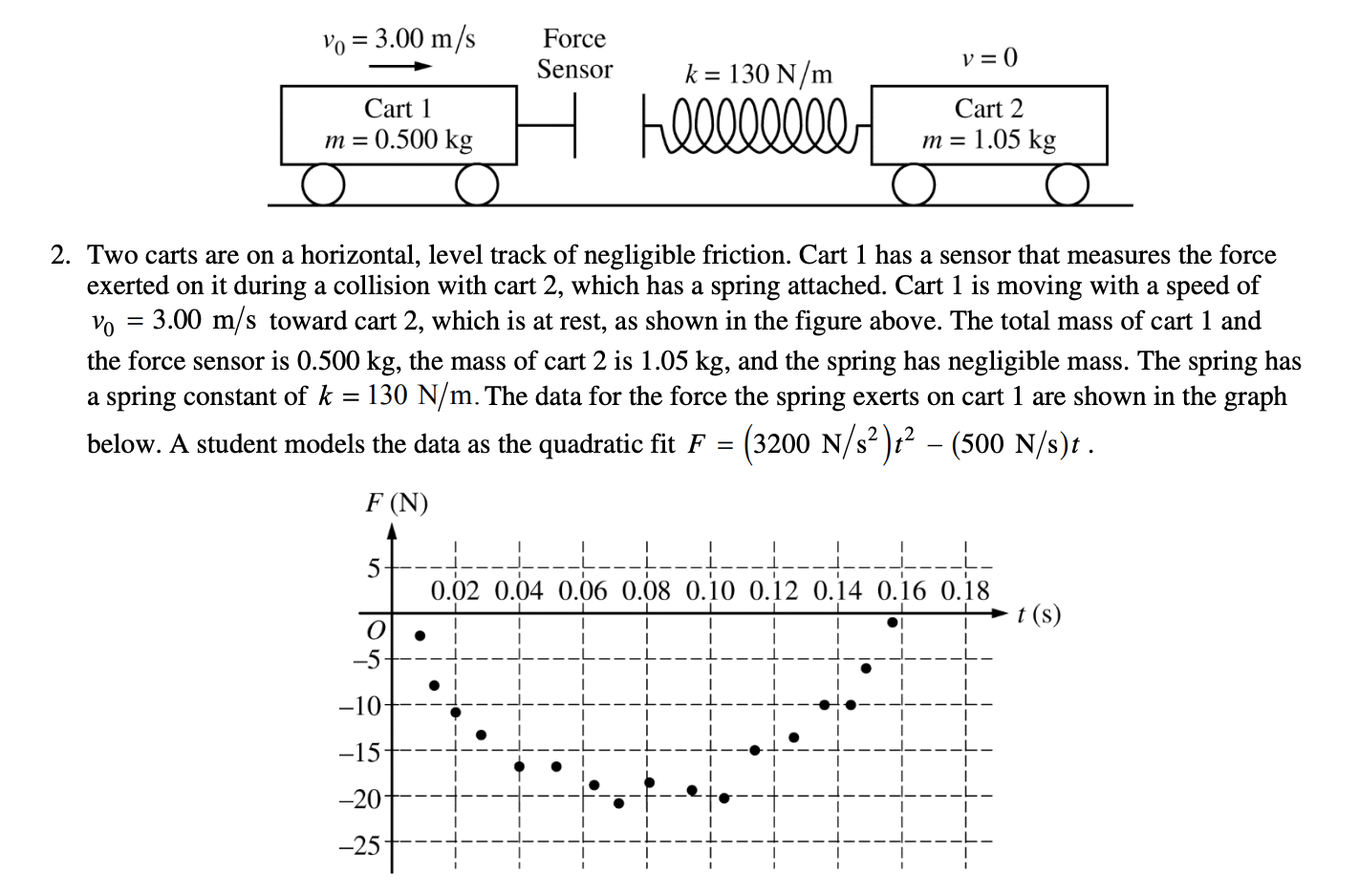
Taken from College Board

(For part 1 you'll need the answer for part a of this question, which is -2.03 N*s)
Answer:
Impulse is equal to the change in momentum, and in this scenario mass is not changing so we can look at this problem with initial and final velocity. Remember that velocity is a vector, so positives and negatives represent direction!


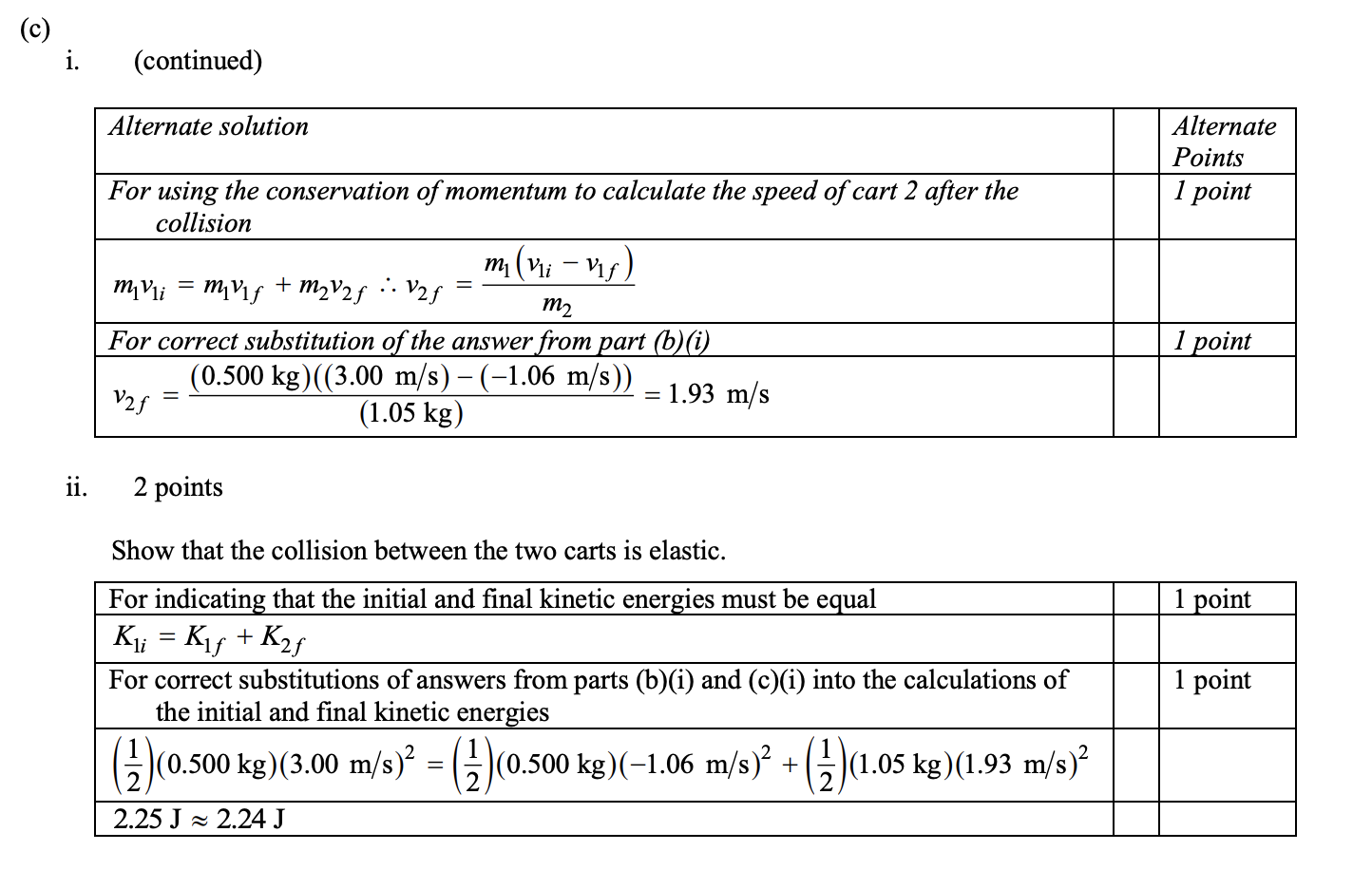
Answer:
Use conservation of momentum to calculate the speed of cart 2. Then, you should recall that kinetic energy is conserved in elastic collisions.

Browse Study Guides By Unit
🚗Unit 1 – Kinematics
🚀Unit 2 – Newton’s Laws of Motion
🎢Unit 3 – Work, Energy, & Power
🎳Unit 4 – Systems of Particles & Linear Momentum
🚲Unit 5 – Rotation
🌊Unit 6 – Oscillations
🪐Unit 7 – Gravitation
📚Study Tools

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.