7.2 Orbits of Planets and Satellites
2 min read•november 7, 2020
Daniella Garcia-Loos
AP Physics C: Mechanics ⚙️
68 resourcesSee Units
7.2 Orbits of Planets and Satellites
One of the most common applications of gravitation that AP enjoys is the orbits of planets and satellites!
Fast Facts of Planets and Satellites in Orbit:
- Angular momentum is conserved
- Mechanical energy is conserved
- GPE is at 0 at an infinite distance away
- “Escape speed” is the minimum speed required to escape the gravitational field
Here is the derivation for Gravitational Potential Energy:
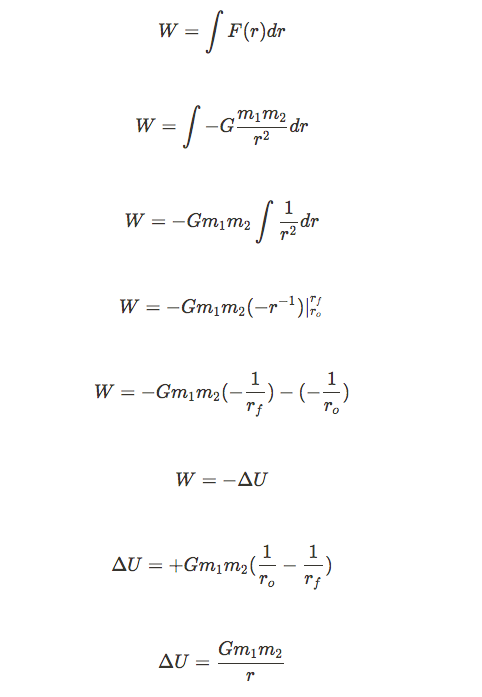
This also means that the kinetic energy of a satellite in orbit can be simplified down to only be dependent on the satellite and its distance.
We can connect centripetal/circular motion to gravitational force too!
The centripetal force acting on a satellite/planet system is caused by the gravitational force.
This means that we can derive some formulas to describe the orbits of these systems that move in a circular path.
Let's try to find tangential velocity:
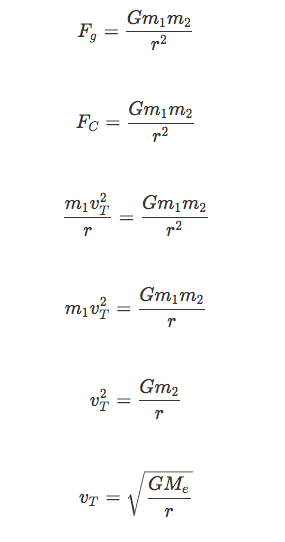
Additionally, I'll leave the proof of this one as an exercise for you, but we can use a similar method to determine the period of the orbit.
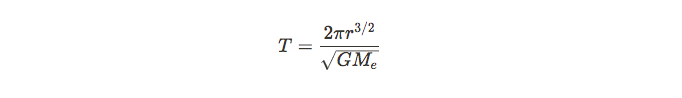
There is another version of this formula which is known as Kepler's Third Law, which is only applicable for objects in circular orbit:
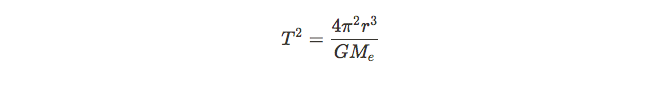
This is commonly rewritten as below in order to simplify the relationship:
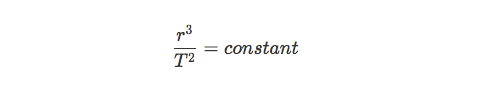
Lastly, in non-orbiting situations in relation to satellites, you can use the conservation of energy in order to help you describe its motion.
Unit 7.2 Practice Problems

Taken from College Board
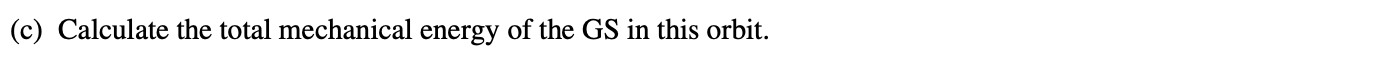
Answer


Answer
Most Physics C: Mechanics classes tend to skip over Kepler's Laws, so note that it is perfectly acceptable to justify your answer with other physics you know.


Answer

Browse Study Guides By Unit
🚗Unit 1 – Kinematics
🚀Unit 2 – Newton’s Laws of Motion
🎢Unit 3 – Work, Energy, & Power
🎳Unit 4 – Systems of Particles & Linear Momentum
🚲Unit 5 – Rotation
🌊Unit 6 – Oscillations
🪐Unit 7 – Gravitation
🙏Exam Reviews

Fiveable
Resources
© 2023 Fiveable Inc. All rights reserved.