Avanish Gupta
Jed Quiaoit
AP Statistics 📊
265 resourcesSee Units
The least squares regression line (LSRL) is the best linear regression line that exists in the sense that it minimizes the sum of the squared residuals. (Remember from previous sections that residuals are the differences between the observed values of the response variable, y, and the predicted values, ŷ, from the model.)
The least squares criterion is used to find the line of best fit because it minimizes the sum of the squared residuals. This is done by minimizing the difference between the observed and predicted values, which in turn maximizes the accuracy of the model.
The least squares regression line is given by the formula ŷ = a + bx, where ŷ is the predicted value of the response variable, x is the predictor or explanatory variable, a is the y-intercept (the value of ŷ when x is zero), and b is the slope (the change in ŷ per unit change in x). The y-intercept and slope can be calculated using the one-variable statistics of x and y.
The reason why the residuals are squared in the least squares criterion is to give more weight to larger residuals and to eliminate the cancellation of positive and negative residuals. Squaring the residuals also has the effect of penalizing larger deviations from the line of best fit more heavily, which can help to reduce the overall variance in the model. 🪢
LSRL—Slope
The slope is the predicted increase in the response variable with an increase of one unit of the explanatory variable. To find the slope, we have the formula: ⛰️
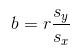
image courtesy of: codecogs.com
(where b is the slope, r is the correlation coefficient between x and y, sy is the standard deviation of y, and sx is the standard deviation of x.)
The least squares estimate of the slope takes into account the variability in both x and y and the strength of the linear relationship between them. It is a weighted average of the deviation of y from the mean of y over the deviation of x from the mean of x, with the correlation coefficient, r, serving as a correction factor.
Template for Interpretation
When asked to interpret a slope of a LSRL, follow the template below:
⭐ "There is a predicted increase/decrease of ______ (slope in unit of y variable) for every 1 (unit of x variable)."
Big Three
- Context
- Word "predicted"
LSRL—y-intercept
Once you have calculated the slope of the least squares regression line, you can use the point-slope form to find the y-intercept and the general formula for the line.
The point-slope form of a linear equation is given by:
ŷ - y1 = m(x - x1)
where ŷ is the predicted value of the response variable, m is the slope of the line, x is the predictor or explanatory variable, and (x1, y1) is a point on the line.
The LSRL always passes through the point (x̄, ȳ), where x̄ is the mean of the predictor variable and ȳ is the mean of the response variable. Therefore, we can use this point to find the y-intercept of the line using the point-slope form.
Substituting the values into the point-slope form, we have:
ŷ - ȳ = b(x - x̄)
Solving for ŷ, we get:
ŷ = bx + (-bx̄ + ȳ)
The expression in parentheses is the y-intercept of the line, which represents the value of the response variable when the explanatory variable is zero. 💛
Template for Interpretation
Template time! When asked to interpret a y-intercept of a LSRL, follow the template below:
⭐ "The predicted value of (y in context) is _____ when (x value in context) is 0 (units in context)."
Big Three
- Context
LSRL—Coefficient of Determination
The coefficient of determination, also known as R-squared, is a statistic that is used to evaluate the fit of a linear regression model (how well the LSRL fits the data). It is a measure of how much of the variability in the response variable (y) can be explained by the model. 🍄
R-squared can be defined as the square of the correlation coefficient (r) between the observed and predicted values of the response variable. It is represented by the symbol R-squared and ranges from 0 to 1, with a value of 0 indicating no relationship between the explanatory and response variables (LSRL does not model the data at all) and a value of 1 indicating a perfect linear relationship.
There is also another formula for r^2 as well. This formula is:

image courtesy of: codecogs.com
This is saying that this is the percent difference between the variance of y and the sum of the residual squared. In other words, this is the reduction in the variation of y due to the LSRL. When interpreting this we say that it is the “percentage of the variation of y that can be explained by a linear model with respect to x.”
Template time yet again! When asked to interpret a coefficient of determination for a least squares regression model, use the template below:
⭐ "____% of the variation in (y in context) is due to its linear relationship with (x in context)."
Big Three
- Context
LSRL—Standard Deviation of the Residuals
The last statistic we will talk about is the standard deviation of the residuals, also called s. S is the typical residual by a given data point of the data with respect to the LSRL. The formula for s is given as: 🐫
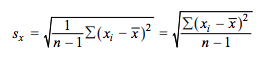
image courtesy of: apcentral.collegeboard.org
which looks similar to the sample standard deviation, except we will divide by n-2 and not n-1. Why? We will learn more about s when we learn inference for regression in Unit 9.
Reading a Computer Printout
On the AP test, it is very likely that you will be expected to read a computer printout of the data. Here is a sample printout with a look at where most of the statistics you will need to use are (the rest you will learn in Unit 9): 🖥️

Courtesy of Starnes, Daren S. and Tabor, Josh. The Practice of Statistics—For the AP Exam, 5th Edition. Cengage Publishing.
💡 Always use R-Sq, NEVER R-Sq(adj)!
🎥 Watch: AP Stats - Least Squares Regression Lines
Practice Problem
A researcher is studying the relationship between the amount of sleep (in hours) and the performance on a cognitive test. She collects data from 50 participants and fits a linear regression model to the data. The summary of the model is shown below:
Summary of Linear Regression Model:
Response variable: Performance on cognitive test (y)
Explanatory variable: Amount of sleep (x)
Slope (b): -2.5
Y-intercept (a): 50
Correlation coefficient (r): -0.7
R-squared: 0.49
a) Interpret the slope of the model in the context of the problem.
b) Interpret the y-intercept of the model in the context of the problem.
c) Interpret the correlation coefficient of the model in the context of the problem.
d) Interpret the R-squared value of the model in the context of the problem.
e) Based on the summary of the model, do you think that the amount of sleep has a significant effect on the performance on the cognitive test? Why or why not?
f) Suppose the researcher collects data from an additional 50 participants and fits a new linear regression model to the combined data. The summary of the new model is shown below:
Slope (b): -1.9
Y-intercept (a): 48
Correlation coefficient (r): -0.6
R-squared: 0.36
Compare the two models and explain how the new model differs from the original model in terms of the strength and direction of the relationship between the amount of sleep and the performance on the cognitive test.
Answers
a) The slope of the model is -2.5, which means that for every one-hour increase in the amount of sleep, the performance on the cognitive test is predicted to decrease by 2.5 points.
b) The y-intercept of the model is 50, which means that the performance on the cognitive test is predicted to be 50 points when the amount of sleep is zero.
c) The correlation coefficient of the model is -0.7, which indicates a strong negative linear relationship between the amount of sleep and the performance on the cognitive test. A negative correlation means that as the amount of sleep increases, the performance on the cognitive test decreases.
d) The R-squared value of the model is 0.49, which means that 49% of the variability in the performance on the cognitive test can be explained by the model. This indicates that the model is able to capture a significant portion of the variance in the data, but there may be other factors that are not being considered that are also contributing to the performance on the cognitive test.
e) Based on the summary of the model, it appears that the amount of sleep has a significant effect on the performance on the cognitive test. The slope of the model is negative, indicating a negative relationship between the variables, and the correlation coefficient is strong (close to -1). However, it is important to note that the R-squared value is not 1, which means that there are other factors that are also influencing the performance on the cognitive test.
f) In the new model, the slope is -1.9, which is slightly less negative than the slope in the original model (-2.5). This suggests that the relationship between the amount of sleep and the performance on the cognitive test is slightly weaker in the new model compared to the original model.
- The y-intercept is also slightly lower in the new model (48) compared to the original model (50).
- The correlation coefficient is slightly weaker in the new model (-0.6) compared to the original model (-0.7).
- Finally, the R-squared value is lower in the new model (0.36) compared to the original model (0.49).
Overall, these differences suggest that the new model has a slightly weaker and less negative relationship between the amount of sleep and the performance on the cognitive test compared to the original model.
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.