📚

All Subjects

📊

AP Stats

🔎

Unit 3

Unit 3 Overview: Collecting Data

7 min read•june 18, 2024

Jed Quiaoit

AP Statistics 📊

265 resources

See Units

How Do We Approach Data Collection?

"Depending on how data are collected, we may or may not be able to generalize findings or establish evidence of causal relationships. For example, if random selection is not used to obtain a sample from a population, bias may result and statistics from the sample cannot be assumed to generalize to the population.

For data collected using well-designed experiments, statistically significant differences between or among experimental treatment groups are evidence that the treatments caused the effect. [You'll] learn important principles of sampling and experimental design in this unit [and] learn about statistical inference in Units 6–9." – College Board, AP Statistics Course Description

In other words, you'll have lots and lots of opportunities throughout this unit to learn about (among many other topics): 🦉

various methods for collecting data, including experiments, surveys, and observational studies.
the different types of sampling techniques, such as simple random sampling, stratified sampling, cluster sampling, and systematic sampling.
bias in data collection and how to minimize it
observational studies and experiments, including how to design and conduct experiments and how to analyze and interpret the results.

Data Collection and "Randomness"

Given that variation may be random or not, conclusions are uncertain.

It's important to consider the role that random variation plays in statistical analysis. While random variation can sometimes make it more difficult to draw conclusions from data, it is not necessarily a problem as long as it is taken into account. 🍀

In fact, random variation is often used to help estimate the precision of statistical conclusions: methods for data collection that do not rely on chance result in untrustworthy conclusions. When data is collected using methods that do not rely on chance, such as convenience sampling or self-selection, it can be difficult to draw reliable conclusions because the data may not be representative of the larger population. In such cases, it's important to carefully consider the potential biases in the data and how they may affect the conclusions that are drawn.

Planning a Study

A population consists of all items or subjects you're interested in, while a sample selected for study is a subset of the aforementioned population. 🏃‍♂️

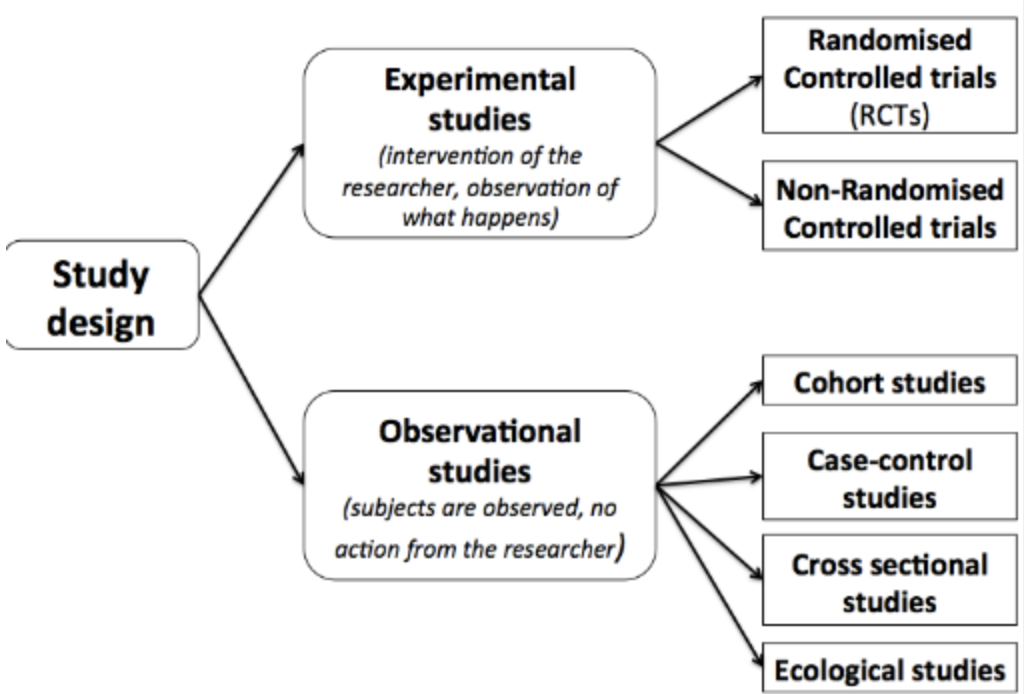
Source: Medium

With such ideas in mind, there are different types of studies:

In an observational study, researchers observe and collect data from a sample of individuals, but they do not manipulate or intervene in any way. Observational studies can be either retrospective, in which researchers look back at data that has already been collected, or prospective, in which researchers collect data as the study is being conducted. A sample survey is a type of observational study that involves collecting data from a sample of individuals in an attempt to learn about the population from which the sample was drawn.

In contrast, an experiment involves manipulating one or more variables and measuring the effect of these manipulations on other variables. Experimental units, such as participants or subjects, are assigned to different conditions or treatments, and the effects of these treatments on the units are measured. Experimental designs allow researchers to establish causal relationships between variables, because they involve manipulating the variables of interest and measuring their effects on other variables.

It's generally more appropriate to make generalizations about a population based on samples that are randomly selected or representative of the population, because random sampling tends to produce a sample that is more representative of the population. If a sample is not representative of the population, it may be difficult to draw reliable conclusions about the population from the sample.

It's also important to note that it is not possible to determine causal relationships between variables using data collected in an observational study. Observational studies are useful for identifying correlations between variables, but they cannot establish causality because they do not involve manipulating the variables of interest. To establish a causal relationship, it is generally necessary to use an experimental design in which the variables of interest are manipulated and their effects on other variables are measured.

Random Sampling and Data Collection

The way data is collected can have a significant impact on what can be concluded about a population. Different data collection methods have different strengths and limitations, and it is important to consider these when interpreting the results of a study. 🎰

Source: Weebly

Sampling without replacement occurs when an item from a population can be selected only once. This means that once an item has been selected, it is not replaced back into the population and is no longer available for selection.

Sampling with replacement, on the other hand, occurs when an item from the population can be selected more than once. This means that after an item is selected, it is replaced back into the population and is available for selection again.

Studies often employ a multitude of sampling methods: ⌛️

A simple random sample (SRS) is a type of random sample in which every member of the population has an equal and independent chance of being selected. This is the most basic and unbiased sampling method, and it is often used as a reference point when comparing the results of other sampling methods.

A stratified random sample is a type of random sample in which the population is divided into subgroups (strata) based on certain characteristics, and a separate random sample is drawn from each stratum. This method is used when the goal is to ensure that the sample is representative of the different subgroups in the population.

A cluster sample is a type of sampling method in which the population is divided into groups (clusters), and a random sample of clusters is selected. All members of the selected clusters are included in the sample. This method is often used when it is impractical or too expensive to sample the entire population individually, but it can introduce bias if the clusters are not representative of the larger population.

A systematic random sample is a type of random sample in which the members of the population are listed in some order, and every nth member is selected for the sample, where n is the sampling interval. This method is easy to implement and can be less expensive than other sampling methods, but it can introduce bias if the list of population members is not truly random.

A census is a study in which data is collected from every member of a population. This method is the most comprehensive and accurate way to collect data, but it can be very expensive and time-consuming to conduct a census.

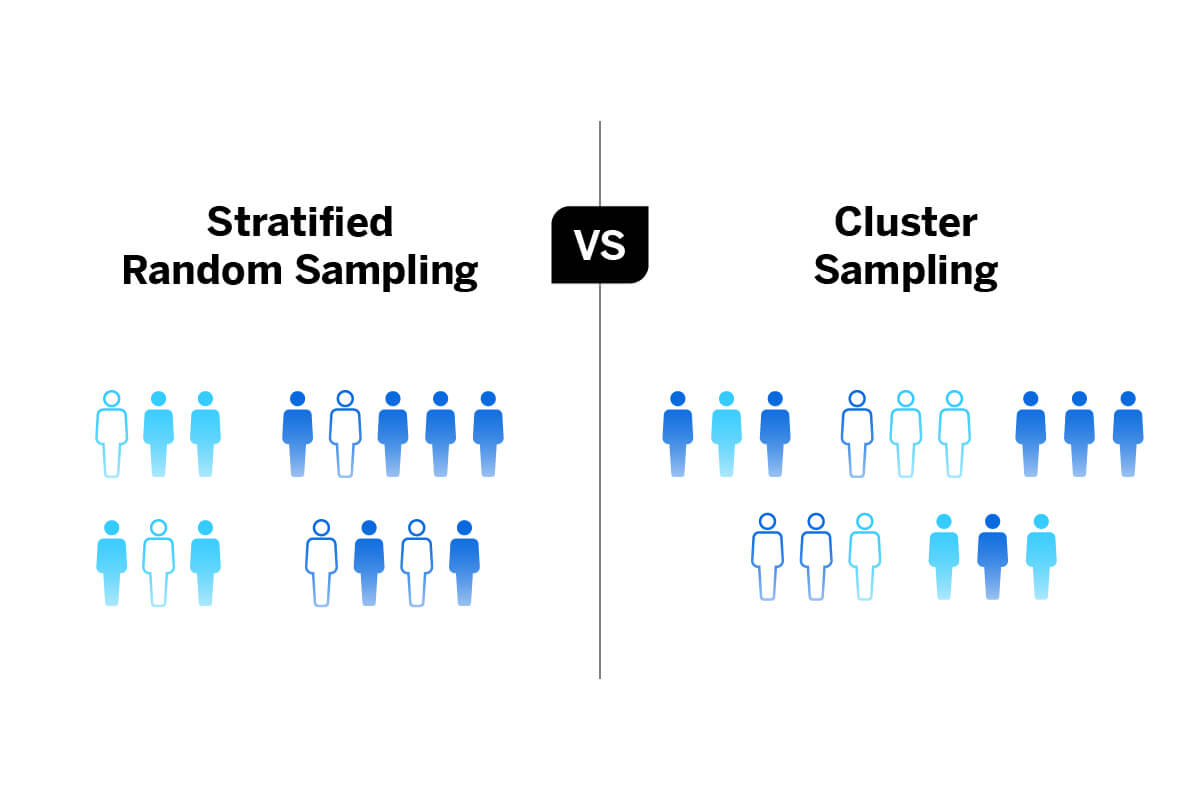
Source: Qualtrics

Biases

Bias occurs when certain responses are systematically favored over others. It can occur in a variety of ways and can have a significant impact on the decisions and actions taken by individuals and organizations. 😔

Source: Statology

Experimental Design

As implied, well-designed experiments can establish evidence of causal relationships. How do we get to that point, then?

First, let's learn more about the components of an experiment:

In an experiment,

The experimental units are the individuals or objects that are being studied.
The explanatory variables, also known as factors, are the variables that are manipulated by the experimenter in order to observe the effect on the response variable.
The response variable is the outcome that is measured, and
The confounding variables are variables that may influence the relationship between the explanatory and response variables, potentially creating a false association.

It is important to control for confounding variables in order to accurately interpret the results of an experiment.

A well-designed experiment should include the following: 🧪

Comparisons of at least two treatment groups, one of which could be a control group.
Random assignment/allocation of treatments to experimental units.
Replication (more than one experimental unit in each treatment group).
Control of potential confounding variables where appropriate.

In a completely randomized experimental design, treatments are randomly assigned to the experimental units, which helps to control for confounding variables. By randomly assigning treatments, you are more likely to have a balanced distribution of confounding variables across the different treatment groups, which can help to isolate the effect of the treatment on the response variable.

This is in contrast to a non-randomized design, where the assignment of treatments may be influenced by other factors, which can make it more difficult to attribute any differences in responses to the treatments.

Another way to control confounding variables is the presence of control groups. A control group is a group of experimental units that is used as a baseline for comparison. The control group may either receive no treatment or receive a placebo, which is an inactive substance that has no therapeutic effect. By comparing the responses of the treatment group(s) to the responses of the control group, you can determine the effect of the treatment on the response variable. Using a control group helps to control for extraneous variables and allows you to isolate the effect of the treatment on the response variable.

Browse Study Guides By Unit

👆Unit 1 – Exploring One-Variable Data

✌️Unit 2 – Exploring Two-Variable Data

🔎Unit 3 – Collecting Data

3.0Unit 3 Overview: Collecting Data