📚

All Subjects

📊

AP Stats

🔎

Unit 3

3.3 Random Sampling and Data Collection

8 min read•december 29, 2022

Kanya Shah

Jed Quiaoit

AP Statistics 📊

265 resources

See Units

As alluded to in earlier sections, the big idea in this unit is that the way we collect data influences what we can and cannot say about a population.

To avoid the effects of bias on your data, the best method of implementing a study is by using random sampling in which a chance process is used to determine which members of a population are included in the sample. 📃

Types of Non-Biased Sampling Methods

Simple Random Sample (SRS)

A simple random sample (SRS) is a sample in which every group of a given size has an equal chance of being chosen. This means that every individual in the population has an equal chance of being selected for the sample, and that the sample is representative of the overall population.

There are several mechanisms that can be used to obtain a simple random sample, including numbering individuals and using a random number generator, using a table of random numbers, or drawing cards from a deck without replacement. These mechanisms ensure that the sample is selected randomly and that every group of a given size has an equal chance of being chosen. 🃏

Simple random sampling is a widely used sampling method because it is relatively easy to implement and provides a representative sample of the population. It is often used as a baseline comparison for other sampling methods, and is the basis for many types of sampling mechanisms. ✔️

In a calculator, SRS chooses a sample size “n” in a way that a group of individuals in the population has an equal chance to be selected as the sample.

Choosing an SRS using a TI-84 Calculator:

Label each individual in the population with a different label from 1 to “N,” where N is the total number of individuals in the population.
Randomize the way you choose the individuals for the sample. Use a random number generator to get “n” different integers from 1 to N, where n is the sample size.
Select the individuals that were chosen by the calculator.

NOTE: When an item from a population can be selected only once, this is called sampling without replacement. When an item from the population can be selected more than once, this is called sampling with replacement.

Stratified Random Sample

Strata are groups of individuals in a population who share characteristics thought to be associated with the variables being measured in a study. 📚

A stratified random sample involves dividing the population into separate strata, based on shared characteristics or attributes. This ensures that the sample is representative of the overall population in terms of these characteristics.

Within each stratum, a simple random sample is then selected using one of the mechanisms described above, such as numbering individuals and using a random number generator or using a table of random numbers. The selected units from each stratum are then combined to form the final sample.

Stratified random sampling is often used when the population is heterogeneous, or diverse, in terms of the characteristics being studied. By dividing the population into strata based on these characteristics, researchers can ensure that the sample is representative of the overall population in terms of these characteristics.

Stratified random samples also reduce variability in the data and give more precise results.

Source: Blogspot

Example

Remember the practice question in the previous section about confounding variables? We could use those as strata!

An example of stratified random sampling might involve conducting a study to investigate the relationship between diet and heart disease. To ensure that the sample is representative of the overall population, the population might be stratified based on age, gender, and income.

We can, then, number individuals and using a random number generator or using a table of random numbers. The selected units from each stratum would then be combined to form the final sample.

This approach would ensure that the sample is representative of the overall population in terms of age, gender, and income, allowing researchers to more accurately interpret the results of the study. It would also allow researchers to investigate any potential interactions between these variables and the relationship between diet and heart disease.

Cluster Sample

A cluster sample involves the division of a population into smaller groups, called clusters. Ideally, there is heterogeneity within each cluster, and clusters are similar to one another in their composition. A simple random sample of clusters is selected from the population to form the sample of clusters. Data are collected from all observations in the selected clusters.

How is this different from stratified sampling? In a cluster sampling design, the population is first divided into smaller groups, or clusters, and a sample of these clusters is selected. Data is then collected from all observations within the selected clusters.

One of the main advantages of cluster sampling is that it can be more cost-effective and efficient than simple random sampling, especially when the population is spread out over a large geographic area. It is also useful when it is difficult to obtain a complete list of the individuals in the population, as is often the case in developing countries or in studying hard-to-reach populations.

However, cluster sampling can also introduce bias if the clusters are not representative of the overall population. It is important to carefully consider the sampling frame and the sampling method to ensure that the sample is representative of the population.

Example

Imagine that you're a researcher who wants to study the attitudes of high school students towards school lunches. You want to study a sample of high schools in a large city to get a sense of the attitudes of students across the city. Instead of sampling students from all the high schools in the city individually (which would be time-consuming and expensive), you decide to use cluster sampling.

First, you divide the high schools in the city into clusters based on geographic location (e.g., north, south, east, west). Then, you randomly select a sample of these clusters (e.g., you might choose two high schools from each geographic location). Finally, you collect data from all the students in the selected high schools to get a sample of students from across the city.

In this example, the population is all high school students in the city, the clusters are the high schools, and the sample is the students in the selected high schools.

Systematic Random Sample

A systematic random sample is unique in which sample members are selected from a population by starting at a randomly chosen point and then selecting every kth element from the sampling frame, where k is the periodic interval.

For example, if you have a list of 1000 people and you want to select a sample of 100 people using a systematic random sample, you might choose a random starting point between 1 and 10, and then select every 10th person on the list (e.g., the 1st person, the 11th person, the 21st person, and so on). This ensures that every member of the population has an equal probability of being selected.

Systematic random sampling is a popular sampling method because it is relatively easy to implement and it can be more efficient than simple random sampling. However, it is important to ensure that the periodic interval (k) is chosen correctly to avoid introducing bias into the sample. For example, if the periodic interval is not chosen randomly, it may result in oversampling or undersampling of certain subgroups within the population.

Example

Imagine that you are a researcher who wants to study the attitudes of grocery store customers towards the store's loyalty program. You want to study a sample of customers from a large grocery store chain to get a sense of the attitudes of customers across the chain. Instead of sampling customers from all the stores in the chain individually (which would be time-consuming and expensive), you decide to use systematic random sampling.

First, you create a list of all the customers who have shopped at the store in the past month. This list will be your sampling frame. Next, you choose a random starting point on the list (e.g., you might choose the 15th person on the list). Finally, you select every 10th person on the list after the starting point (e.g., the 15th person, the 25th person, the 35th person, and so on). This will give you a sample of customers from across the chain.

In this example, the population is all customers who have shopped at the store in the past month, the sampling frame is the list of customers, and the sample is the customers selected according to the periodic interval.

Altogether, being able to identify which method to use depends on what the question is asking. Identify the population and variables to figure out how large of a difference there is between the sample. Make your decision based on that information.

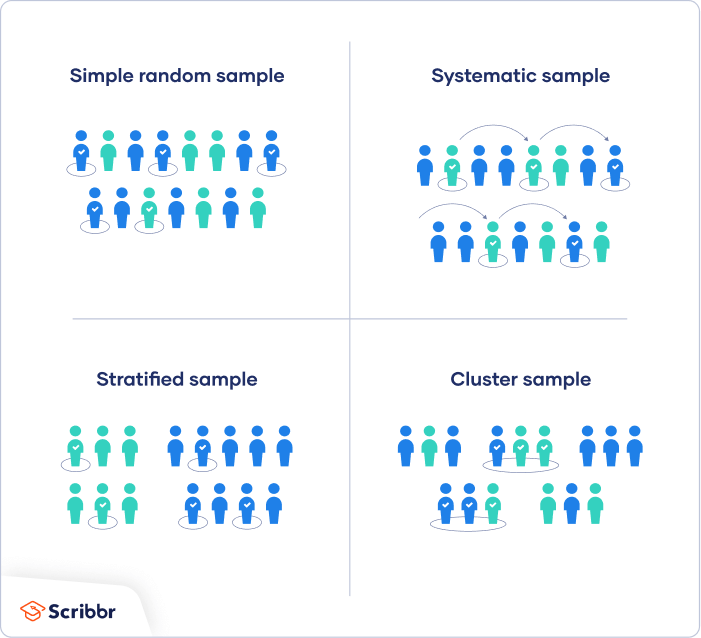
Source: Scribbr

Practice Problem

You are a researcher who wants to study the attitudes of college students towards climate change. Your goal is to get a sense of the attitudes of college students across the United States. You have a budget of $10,000 and six months to complete the study.

There are three potential sampling methods that you could use:

Simple random sampling: You could create a list of all the college students in the United States and use a random number generator to select a sample of students from the list. This method would ensure that every student in the population has an equal chance of being selected, but it would be time-consuming and expensive to create a complete list of all the college students in the United States.
Cluster sampling: You could divide the college students in the United States into clusters based on geographic location (e.g., east coast, west coast, midwest) and randomly select a sample of these clusters. You could then collect data from all the students in the selected clusters. This method would be more efficient and cost-effective than simple random sampling, but it could introduce bias if the clusters are not representative of the overall population.
Systematic random sampling: You could create a list of all the college students in the United States and choose a random starting point on the list. You could then select every 100th student on the list after the starting point to get a sample of students from across the United States. This method would be relatively easy to implement and could be more efficient than simple random sampling, but it could introduce bias if the periodic interval (100 students) is not chosen randomly.

Which sampling method do you think would be the best to use in this situation, and why?

Answer

In this situation, cluster sampling might be the best method to use because it would be more efficient and cost-effective than simple random sampling, and it would not require creating a complete list of all the college students in the United States. However, it is important to ensure that the clusters are representative of the overall population to avoid introducing bias into the sample.

Here's the fun part: AP Stats graders are actually open-minded if you picked either simple random sampling or systematic random sampling (instead of cluster sampling). Your job is to create a very persuasive argument that'll convince them that either sampling method might work, too (in comparison to the other two)!

🎥 Watch: AP Stats - Sampling Methods and Sources of Bias

Browse Study Guides By Unit

👆Unit 1 – Exploring One-Variable Data

✌️Unit 2 – Exploring Two-Variable Data

🔎Unit 3 – Collecting Data

3.0Unit 3 Overview: Collecting Data

3.1Introducing Statistics: Do the Data We Collected Tell the Truth?

3.2Introduction to Planning a Study

3.3Random Sampling and Data Collection

3.4Potential Problems with Sampling

3.5Introduction to Experimental Design

3.6Selecting an Experimental Design