📚

All Subjects

📊

AP Stats

🔎

Unit 3

3.6 Selecting an Experimental Design

8 min read•june 18, 2024

Jed Quiaoit

Aly Moosa

AP Statistics 📊

265 resources

See Units

Selecting the proper experimental design depends on the situation presented and the experimental units given. You need to be able to identify when it is appropriate to utilize a certain type of experiment. Make sure you understand the differences between the types of experiments and how to create the treatment groups randomly and you'll be a master of experimental design in no time! 🤠

Essential Knowledge

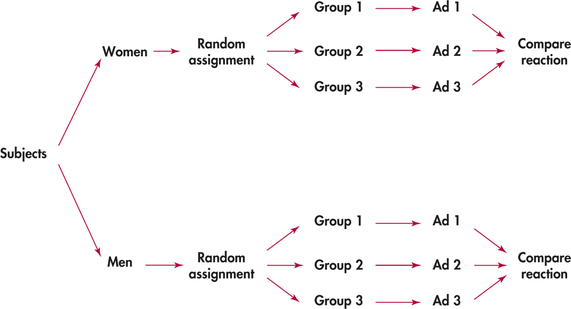
While completely randomized designs are the simplest statistical designs for experiments, there are times when the simplest method for yielding precise results is not completely randomized. There are three main designs that you can use after selecting a sample for your experiment. Don't mix up language of experiment and the language of sample surveys! ❗

The Big Three

Completely Randomized Design - Experimental units are randomly assigned to treatments equally by chance.
Blocking Design - Sort groups of individuals that are known to be similar in some way that can expect different results. Do not randomize those groups together. USE ALL BLOCKS in a blocked experiment.
Matched Pairs Design - A common type of block for comparing two treatments with similar individuals or identical treatment methods.

Longer explanations below:

In a completely randomized design, experimental units are randomly assigned to treatments equally by chance. This means that each unit has an equal probability of being assigned to any of the treatment groups, and the treatment groups are similar in terms of known confounding variables. A completely randomized design is useful for studying the effects of one or more treatments on a response variable, without considering the influence of other variables.

In a blocking design, experimental units are sorted into groups (called blocks) based on a variable that is known to influence the response variable. The units within each block are expected to be similar to each other with respect to this variable. The treatments are then randomly assigned to the units within each block. By using a blocking design, researchers can control for variables that may influence the response variable and reduce the potential for bias.

A matched pairs design is a special case of a blocking design in which experimental units are arranged in pairs that are matched on relevant factors, such as age, gender, or other characteristics. The pairs are then given both treatments, either by randomly assigning one treatment to one member of the pair and the other treatment to the second member of the pair, or by giving each subject both treatments. A matched pairs design is useful for comparing the effects of two treatments on a response variable, while controlling for known confounding variables.

Practice Problems

(1) A researcher is interested in studying the effectiveness of a new teaching method for high school math students. The researcher plans to randomly assign 50 students to either the control group or the experimental group. The control group will receive the traditional teaching method, while the experimental group will receive the new teaching method.

At the end of the study, the researcher will administer a math achievement test to all of the students. The researcher will then compare the mean math achievement scores of the two groups to determine if the new teaching method is more effective than the traditional method.

The researcher wants to use a completely randomized design for this study.

Write a detailed plan for how the researcher should set up the completely randomized design, including how the students should be assigned to the control and experimental groups.

(2) A researcher is interested in studying the effectiveness of a new study technique on college students' grades. The researcher plans to recruit 100 students from a large university and randomly assign them to either the control group or the experimental group. The control group will receive the traditional study technique, while the experimental group will receive the new study technique.

However, the researcher is aware that students' grades can be affected by their major and the difficulty of their course load. To control for these factors, the researcher wants to use a blocking design in the study.

Write a detailed plan for how the researcher should set up the blocking design, including how the students should be assigned to the control and experimental groups and how the researcher should control for major and course load.

(3) A researcher is interested in studying the effectiveness of a new study technique on college students' grades. The researcher plans to recruit 100 students from a large university and randomly assign them to either the control group or the experimental group. The control group will receive the traditional study technique, while the experimental group will receive the new study technique.

The researcher is considering using a completely randomized design, a blocking design, or a matched pairs design for the study.

Write a detailed explanation of the advantages and disadvantages of each design and recommend which design the researcher should use, providing a rationale for your recommendation.

Answers

(1) To set up the completely randomized design for this study, the researcher should first compile a list of all 50 students who will participate in the study. The researcher should then randomly assign each student to either the control group or the experimental group using a random number generator or a computer program that generates random assignments.

Once the students have been randomly assigned to the two groups, the researcher should begin implementing the two different teaching methods. The control group should receive the traditional teaching method, while the experimental group should receive the new teaching method.

After the study has been completed, the researcher should administer the math achievement test to all of the students. The researcher should then calculate the mean math achievement scores for both the control and experimental groups.

To determine if the new teaching method is more effective than the traditional method, the researcher should compare the mean math achievement scores of the two groups. If the mean score for the experimental group is significantly higher than the mean score for the control group, the researcher can conclude that the new teaching method is more effective.

or (in bullet form)

Compile a list of all 50 students who will participate in the study
Randomly assign each student to either the control group or the experimental group using a random number generator or a computer program that generates random assignments
Implement the two different teaching methods: traditional method for the control group, new method for the experimental group
Administer a math achievement test to all of the students
Calculate the mean math achievement scores for both the control and experimental groups
Compare the mean scores to determine if the new teaching method is more effective than the traditional method

(2)

To set up the blocking design, the researcher should first gather information on each student's major and course load. The researcher could do this by collecting data on the students' transcripts or by administering a survey to the students.

Next, the researcher should divide the students into groups based on their major and course load. For example, the researcher could create blocks for students with similar majors (e.g. biology, psychology, engineering) and blocks for students with similar course loads (e.g. heavy, moderate, light).

Within each block, the researcher should randomly assign students to either the control group or the experimental group using a random number generator or a computer program that generates random assignments. This will ensure that the two groups are balanced within each block in terms of major and course load.

Once the students have been randomly assigned to the two groups within each block, the researcher should begin implementing the two different study techniques. The control group should receive the traditional study technique, while the experimental group should receive the new study technique.

At the end of the study, the researcher should collect data on the students' grades and compare the mean grades of the two groups to determine if the new study technique is more effective than the traditional technique.

or (in bullet form)

Gather information on each student's major and course load
Divide the students into groups based on their major and course load (e.g. biology major, heavy course load; psychology major, moderate course load)
Within each block, randomly assign students to either the control group or the experimental group using a random number generator or a computer program that generates random assignments
Implement the two different study techniques: traditional technique for the control group, new technique for the experimental group
Collect data on the students' grades and compare the mean grades of the two groups to determine if the new study technique is more effective than the traditional technique

(3)

A completely randomized design involves randomly assigning the participants to the two groups without considering any other factors. The advantage of this design is that it is simple and easy to implement. However, it is not always the best choice because it does not control for any extraneous variables that could affect the outcome of the study.
A blocking design involves dividing the participants into groups based on a particular factor (called a "blocking variable") and then randomly assigning participants within each group to the two treatment conditions. This design is useful when there are variables that the researcher wants to control for but cannot manipulate. The advantage of this design is that it can help reduce the influence of extraneous variables on the outcome of the study. However, it requires more advanced planning and may not always be feasible depending on the available resources and the number of participants.

A matched pairs design involves pairing participants based on a particular factor (such as age, gender, or ability level) and then randomly assigning one member of each pair to the control group and the other member to the experimental group. This design is useful when the researcher wants to control for a specific variable and has a small number of participants. The advantage of this design is that it can reduce the influence of extraneous variables on the outcome of the study. However, it can be time-consuming and may not always be feasible depending on the available resources and the number of participants.

In this case, the researcher should consider using a blocking design. The blocking design would allow the researcher to control for factors such as major and course load that could affect the students' grades. Additionally, the blocking design would be more practical than the matched pairs design, as it would not require pairing students and would be more feasible with a larger number of participants. However, the researcher should carefully consider the resources and time available before deciding which design to use.

Browse Study Guides By Unit

👆Unit 1 – Exploring One-Variable Data

✌️Unit 2 – Exploring Two-Variable Data

🔎Unit 3 – Collecting Data

3.0Unit 3 Overview: Collecting Data

3.1Introducing Statistics: Do the Data We Collected Tell the Truth?

3.2Introduction to Planning a Study

3.3Random Sampling and Data Collection

3.4Potential Problems with Sampling

3.5Introduction to Experimental Design

3.6Selecting an Experimental Design

3.7Inference and Experiments