5.1 Introducing Statistics: Why Is My Sample Not Like Yours?
5 min read•june 18, 2024
Jed Quiaoit
B
Brianna Bukowski
Josh Argo
AP Statistics 📊
265 resourcesSee Units
Sampling Distributions... Defined
A sampling distribution is a distribution of all possible samples of a given size drawn from a population. It represents the distribution of statistics (such as the mean or proportion) calculated from these samples. 💠
For example, suppose you're interested in estimating the mean income of a population of workers. You can take a sample of workers and calculate the mean income of the sample. However, this sample mean is likely to be different from the population mean due to sampling error. To account for this, you can take multiple samples of the same size and calculate the mean income for each sample. The distribution of these sample means is called the sampling distribution of the mean.
In the previous units, every distribution consisted of one sample, such as a class of students grade in a class. With a sampling distribution, you take the average of all means (quantitative) or proportions (categorical) of each possible sample size (n) and use these averages as your data points. The normal model now also represents the distribution of all possible samples of a given sample size.
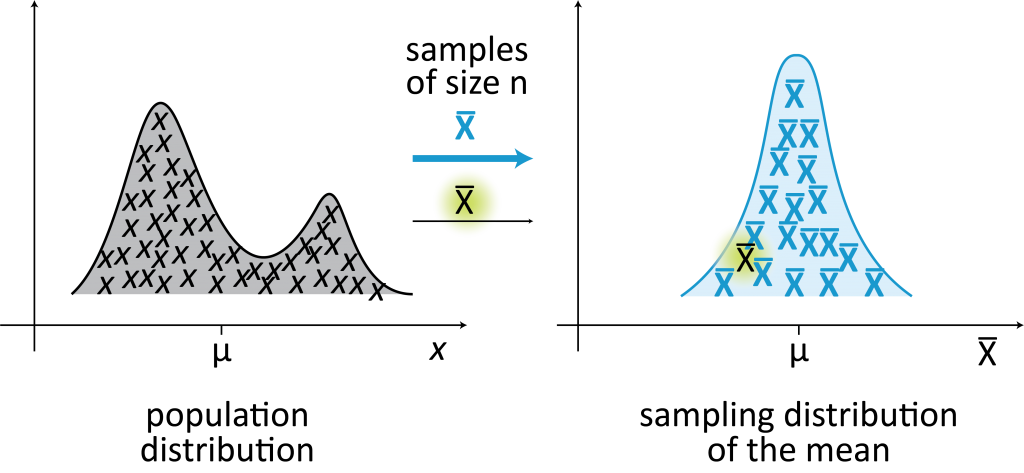
Source: Creative Maths
Differences
To find the sampling distribution for differences in a sample proportion or mean, remember that variances always add to find the new variance. If one needs the standard deviation, you should take the square root of the variance. However, for means you can just subtract. ➖
Discrete vs. Continuous Random Variables
There are two major types of random variables in AP Statistics: discrete and continuous. Discrete random variables are variables that have a certain and definite set of values that the variable could be. Usually, these are whole numbers in real world situations (1, 2, 3, 4, 5…, 100, etc.). For discrete random variables, to calculate the mean, you use the expected variable formula:
Source: AP Statistics Formula Sheet, NEW FOR 2020
For discrete random variables, to calculate the standard deviation, you use a formula similar (in a way) to the expected value formula, but with a square root:.
Source: AP Statistics Formula Sheet, NEW FOR 2020
The other type of random variable, continuous random variables, can take on any value at any point along an interval. Generally, continuous random variables can be measured while discrete random variables are counted. A histogram is used to display continuous data, while a bar graph displays discrete data! 📊
Parameters vs. Statistics
A population parameter is a measure of a characteristic of a population, such as the mean or proportion of a certain attribute. It is a fixed value that represents the true value of the population. 🌎
A sample statistic is a measure of a characteristic of a sample, such as the mean or proportion of a certain attribute. It is a calculated value that estimates the value of the population parameter. 🏠
In AP Statistics, you will be asked to compare Statistics from a Sample to the Parameters of a Population. Here is a chart to help you remember which symbols are from sample statistics and from population parameters:
Measurement | Population Parameter | Sample Statistic |
Mean | 𝝁 | x̅ |
Standard Deviation | σ | s |
Proportions | 𝝆 | p̂ |
Practice Problems
(1) A study is conducted to estimate the proportion of students in a school district who have access to the internet at home. A sample of 1000 students is selected from the school district, and it is found that 750 students have access to the internet at home. Is the proportion of students with internet access at home a parameter or a statistic?
(2) The mean height of all adult males in the United States is 70 inches. Is the mean height of adult males a parameter or a statistic?
(3) A survey is conducted to estimate the proportion of adults in a city who have a college degree. A sample of 500 adults is selected from the city, and it is found that 300 adults have a college degree. Is the proportion of adults with a college degree a parameter or a statistic?
(4) The mean income of all households in the United States is $50,000 per year. Is the mean income of households a parameter or a statistic?
(5) A study is conducted to estimate the proportion of employees in a company who are satisfied with their job. A sample of 200 employees is selected from the company, and it is found that 150 employees are satisfied with their job. Is the proportion of employees who are satisfied with their job a parameter or a statistic?
Answers
(1) The proportion of students with internet access at home is a statistic, because it is calculated from a sample of students and is used to estimate the value of the population parameter (the proportion of all students in the school district with internet access at home).
(2) The mean height of adult males is a parameter, because it is a fixed value that represents the true value of the population (all adult males in the United States).
(3) The proportion of adults with a college degree is a statistic, because it is calculated from a sample of adults and is used to estimate the value of the population parameter (the proportion of all adults in the city with a college degree).
(4) The mean income of households is a parameter, because it is a fixed value that represents the true value of the population (all households in the United States).
(5) The proportion of employees who are satisfied with their job is a statistic, because it is calculated from a sample of employees and is used to estimate the value of the population parameter (the proportion of all employees in the company who are satisfied with their job).
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.