📚

All Subjects

📊

AP Stats

⚖️

Unit 6

6.5 Interpreting p-Values

5 min read•january 3, 2023

Josh Argo

Jed Quiaoit

AP Statistics 📊

265 resources

See Units

image courtesy of: imgflip.com

What is a p-value? 🧐

The p-value of a significance test is a measure of the probability of obtaining a sample with a test statistic that is at least as extreme as the one observed, under the assumption that the null hypothesis is true. In other words, it's the proportion of possible samples of a given size that are equal to or less than/greater than our given sample. 🧺

It is used to help determine whether the observed results are statistically significant or not.

If the p-value is small, it suggests that the observed sample is unlikely to have occurred by chance, and therefore provides evidence against the null hypothesis. 👍
On the other hand, if the p-value is large, it suggests that the observed sample is not significantly different from what we would expect to see by chance alone, and therefore does not provide strong evidence against the null hypothesis. 👎

Here's how the College Board defines p-values:

The p-value is the "proportion of values for the null distribution that are as extreme or more extreme than the observed value of the test statistic." This is

The proportion at or above the observed value of the test statistic, if the alternative is >.
The proportion at or below the observed value of the test statistic, if the alternative is <.
The proportion less than or equal to the negative of the absolute value of the test statistic plus the proportion greater than or equal to the absolute value of the test statistic, if the alternative is ≠.

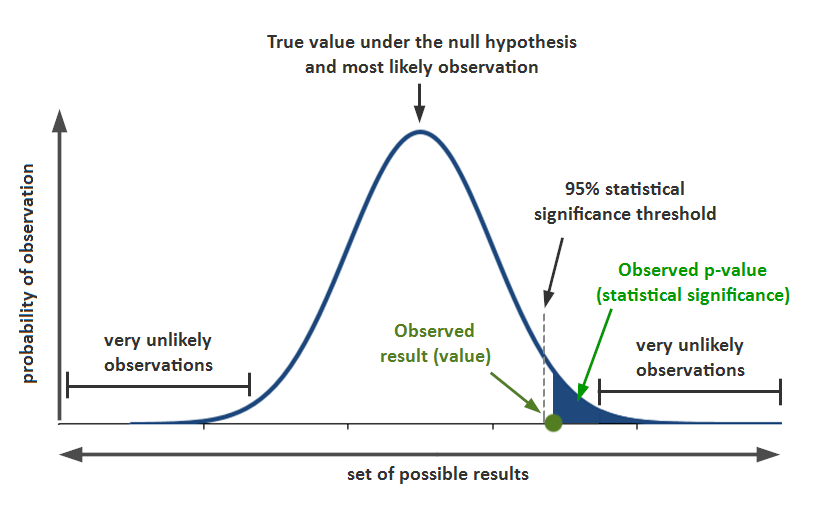
Source: Simply Psychology

How do we interpret a p-value?

If our p-value is low, this means that it is highly unlikely that our sample would be chosen randomly. This could be due to one of three things: 🤷

Legitimate random chance. (I mean, someone wins the lottery every now and then right? 🤑)
Some form of sampling bias. (This is why we check that our sample is random before proceeding to a significance test!)
Our hypothesized value in the null hypothesis is actually false. This is what we are checking with our significance test.

To be sure that this didn't occur by random chance, we should maybe check 2 or 3 random samples. If we get the same result each time, the consistency leads us to believe we are up to something (no one wins the lottery three times in a row). To be sure it isn't sampling bias, we make sure we have random samples. If both of those are met, there must be a problem with null hypothesis value.

Again, it's important to remember that the p-value is computed under the assumption that the null hypothesis is true. Therefore, when interpreting the p-value of a significance test, it's important to consider the context in which the test was conducted and the implications of the null hypothesis being true! ⚠️

For example, in a one-sample proportion test, the null hypothesis typically states that the true population proportion is equal to a particular value (usually 0.5, or no difference from the hypothesized value). If the p-value is small, it suggests that the observed sample proportion is significantly different from the hypothesized value, and provides evidence against the null hypothesis. In this case, you might conclude that the true population proportion is different from the hypothesized value.

On the other hand, if the p-value is large, it suggests that the observed sample proportion is not significantly different from the hypothesized value, and does not provide strong evidence against the null hypothesis. In this case, you might conclude that there is insufficient evidence to reject the null hypothesis and that the true population proportion is equal to the hypothesized value.

Example

In the recent issue of Sports Unlimited, Jackie reads that a right-handed hockey player scores on approximately 5% of their shots. To test this claim, Jackie watches 15 random hockey games and records 921 shots from random, right-handed hockey players. She finds that they scored on 60 of those shots. After calculating her z-score and p-value, she finds that her p-value is essentially 0.017. Interpret this p value. 🏒

This p-value means that of all possible samples of 921 shots from right handed players, approximately 1.7% of those samples would have at least 60 shots. This sample was random from the given information, so no obvious sampling bias. It could be that Jackie just hit the jackpot and watched the right players to have such a high goal scoring percentage. She could check this by redoing the experiment a few times.

The other option is that the 5% isn't actually correct. Maybe that hypothesized percentage is a bit higher... 🤔

🎥 Watch: AP Stats - Inference: Hypothesis Tests for Proportions

Practice Problem

A political campaign is trying to determine whether the proportion of registered voters in their district who support their candidate is significantly different from the overall national proportion of 50%. They conduct a survey by randomly sampling 1000 registered voters in their district and ask whether they support their candidate. They find that 540 out of the 1000 respondents support their candidate. 📋

a) Write the null and alternative hypotheses for this scenario.

b) After conducting a one-sample z-test to determine whether the proportion of registered voters in the district who support the candidate is significantly different from the national proportion of 50%, you find that the p-value for this one-sample z-test is 0.031. Based on the results of the z-test and the p-value, what can the campaign conclude about the proportion of registered voters in the district who support their candidate? What are the limitations of this conclusion?

Answer

a) Null hypothesis: The proportion of registered voters in the district who support the candidate is equal to the national proportion of 50%.

H0: p = 0.50

Alternative hypothesis: The proportion of registered voters in the district who support the candidate is significantly different from the national proportion of 50%.

Ha: p ≠ 0.50

b) Based on the results of the z-test, the campaign can conclude that the proportion of registered voters in the district who support their candidate is significantly different from the national proportion of 50%, because the p-value of 0.031 is smaller than the commonly used significance level of 0.05.

This suggests that the proportion of registered voters in the district who support the candidate is higher than the national proportion. However, it's important to note that this conclusion is based on the assumption that the null hypothesis (that the proportion of registered voters in the district who support the candidate is equal to the national proportion of 50%) is true.

Browse Study Guides By Unit

👆Unit 1 – Exploring One-Variable Data

✌️Unit 2 – Exploring Two-Variable Data

🔎Unit 3 – Collecting Data

🎲Unit 4 – Probability, Random Variables, & Probability Distributions

📊Unit 5 – Sampling Distributions

⚖️Unit 6 – Proportions

6.0Unit 6 Overview: Inference for Categorical Data: Proportions

6.1Introducing Statistics: Why Be Normal?

6.2Constructing a Confidence Interval for a Population Proportion

6.3Justifying a Claim Based on a Confidence Interval for a Population Proportion

6.4Setting Up a Test for a Population Proportion