📚

All Subjects

📊

AP Stats

⚖️

Unit 6

6.4 Setting Up a Test for a Population Proportion

5 min read•june 18, 2024

Jed Quiaoit

Josh Argo

AP Statistics 📊

265 resources

See Units

image courtesy of: imgflip.com

Hypotheses

When it has been identified that we need to perform a one-proportion z-test for a population proportion, the first step we need to do is write out our hypotheses. We have two hypotheses to write: our null hypothesis and our alternative hypothesis.

(1) Null ("H0")

In a statistical hypothesis test, our null hypothesis is the hypothesis based on our claim that was given in the problem. The null hypothesis is a statement about the population parameter that is being tested. It is the situation that is assumed to be true unless there is evidence to the contrary. The null hypothesis is usually a statement of no difference or no relationship between variables. The null is always written as p =____.

For example, if the null hypothesis is that the population proportion is 0.5, this means that it is assumed to be true that the population proportion is 0.5 (p = 0.5) unless there is evidence to the contrary. If the sample proportion is significantly different from 0.5, this would provide evidence against the null hypothesis and suggest that the population proportion is not 0.5.

Remember, if our null hypothesis is true, there is no wow factor, nothing new to claim and essentially, it appears that the original claim was true. ✳️

(2) Alternative ("Ha")

Our alternate hypothesis is the hypothesis that the claim in our null is not true. It is always written as either p <____, p >____ or p ≠_____. The alternative hypothesis is usually a statement of difference or relationship between variables. If we are testing that the actual proportion is less than or greater than the claimed proportion, we are doing a one tailed z-test. If we are testing that the actual proportion is not equal to the claimed proportion, we are doing a two tailed z-test.

If the evidence supports the alternative hypothesis, the null hypothesis is rejected in favor of the alternative hypothesis. If the evidence does not support the alternative hypothesis, the null hypothesis is not rejected. ✳️

💡 SUMMARY:

For hypotheses about parameters, the null hypothesis contains an equality reference (=, ≥, or ≤), while the alternative hypothesis contains a strict inequality (<, >, or ≠). The type of inequality in the alternative hypothesis is based on the question of interest.
Alternative hypotheses with < or > are called one-sided, and alternative hypotheses with ≠ are called two-sided. Although the null hypothesis for a one-sided test may include an inequality symbol, it is still tested at the boundary of equality.

Example

An article recently published in Real News Online! states that 94% of all people can identify the pop culture icon, Baby Yoda. To test this claim, we poll a random sample of 750 people and find that 700 of them can correctly identify Baby Yoda. Do the data give significant evidence that the actual proportion of people who can identify Baby Yoda is more than 94%?

For this question, we are clearly testing a population claim using the sample that we have collected. This calls for a one sample z test for population proportion (or 1-Prop Z Test). Our first step is to write our hypotheses:

H0: p = 0.94
Ha: p < 0.94

Conditions

Random

As with any hypothesis test or confidence interval, we must have a random sample to perform our test. If we do not have a random sample, we can not infer anything about the population because our sample might be biased. There is no way to fix sampling bias using mathematical calculations. If our sample is biased, the whole study might as well be thrown out. 🙁

Independent

Since we are sampling without replacement, we need to make sure that our population is large enough that our experimental units is not really affecting each other after they are selected. To be sure of this, we can use the 10% condition, which states that the population should be at least 10 times the size of the sample. To show this, we can state: "Since it is reasonable to believe that our population is at least 10n, we can assume our sample is independent.

Normal

Since we will be using the normal curve to calculate the probability of obtaining our sample, we must first prove that the sampling distribution is normal. For proportions, we will use the Large Counts Condition, which states the expected numbers of successes and failures is at least 10.

Example

In our example above, we would check the three conditions like this:

Random: "we poll a random sample of 750 people"
Independent: It is reasonable to believe that there are at least 7500 people in the world (obviously true!) 😉
Normal: 750 (0.94) = 658, 750 (0.06) = 45. Both 658 and 45 are more than 10, so we're good. 😊

Calculating Our Necessary Statistics

For actually calculating the values associated with our test, we have to calculate our critical value and from that, we can calculate our p-value. 📱

Z-Score

The z-score for our data is based on the standard normal curve for our sampling distribution. In other words, we are going to see where our sample falls in the range of all possible samples of size n.

For our example above, our observed value was 0.93333. Our expected value was 0.94.

Our standard deviation is calculated just like that of a sampling distribution:

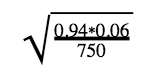
which comes out to be 0.00867.

Putting it all together, our z score comes out to be -0.769.

P-Value

To calculate our p-value, we are going to use our z-score and see the probability of obtaining that sample by using the standard normal curve and calculating the probability of receiving such a z-score (or higher/lower). 🅿️

For the example above, we would use our z-score of -0.769 and find the probability of receiving that (or something lower). One way to do this is to use a calculator with the normalcdf function.

Calculating our p-value with this z-score would look like this:

normalcdf(-100000, -0.769, 0, 1) = 0.221.

Using Technology

If this sounds like a lot of work for one problem, you're in luck! 🍀

Our graphing calculator will do all of this for us! We just need to go to the Stats Tests Menu and select 1-Prop Z-Test. From there, we simply enter in our parameters and our calculator will give us a z-score and p-value automatically! 👏

🎥 Watch: AP Stats - Inference: Hypothesis Tests for Proportions

Browse Study Guides By Unit

👆Unit 1 – Exploring One-Variable Data

✌️Unit 2 – Exploring Two-Variable Data

🔎Unit 3 – Collecting Data

🎲Unit 4 – Probability, Random Variables, & Probability Distributions

📊Unit 5 – Sampling Distributions

⚖️Unit 6 – Proportions

6.0Unit 6 Overview: Inference for Categorical Data: Proportions

6.1Introducing Statistics: Why Be Normal?

6.2Constructing a Confidence Interval for a Population Proportion

6.3Justifying a Claim Based on a Confidence Interval for a Population Proportion