7.2 Constructing a Confidence Interval for a Population Mean
5 min read•june 18, 2024
Jed Quiaoit
Josh Argo
AP Statistics 📊
265 resourcesSee Units
The t-distribution is a continuous probability distribution that is used to estimate population parameters when the sample size is small and the population variance is unknown. It is similar to the normal distribution, but has heavier tails, which means that it is more likely for observations to fall in the extreme tails of the distribution. This is because the t-distribution accounts for the additional uncertainty introduced by estimating the population variance from the sample variance. 🚆
The degrees of freedom (df) in the t-distribution refer to the number of observations in the sample that are free to vary. In other words, it is the number of observations in the sample that are used to estimate the population variance.
As the degrees of freedom increase, the t-distribution becomes more and more similar to the normal distribution, and the area in the tails decreases. This is because with a larger sample size, the sample variance is a more accurate estimate of the population variance, and there is less uncertainty in the distribution of the sample mean.
Because σ (population standard distribution) is typically not known for distributions of quantitative variables, the appropriate
confidence interval procedure for estimating the population mean of one quantitative variable for one sample is a one-sample t-interval for a mean.
Conditions for Inference
Before proceeding to calculate a confidence interval, we have to check that our sampling distribution we are using meets some conditions:
(1) Random Sample
This reduces any bias that may be caused from taking a bad sample
When answering inference questions, it is always essential to make note that our sample was random, either by highlighting text on the exam, or by quoting the problem where it details its randomness. 💬
(2) Independence
This ensures that each subject in our sample was not influenced by the previous subjects chosen. While we are sampling without replacement, if our sample size is not super close to our population size, we can conclude that the effect it has on our sampling is negligible. We can check this condition by questioning if it is reasonable to believe that the population in question is at least 10 times as large as our sample. 💙
A good way to state this when performing inference is to say, "It is reasonable to believe that our population (in context) is at least 10n"
For example, if we have a random sample of 85 teenagers math grades and we are creating a confidence interval for what the average of ALL teenager math grades are, we could state, "It is reasonable to believe that there are at least 850 teenagers currently enrolled in a math class."
(3) Normal
This check verifies that we are able to use a normal curve to calculate our probabilities using either empirical rule or z scores. We can verify that a sampling distribution is normal using the Central Limit Theorem which states that if our sample size is at least 30, we can assume that the sampling distribution will be approximately normal. Normality with our sampling distribution can also be assumed if it is given that the population distribution is normally distributed. 🔔
With our example with 85 teenagers, we can assume that the sampling distribution of 85 teenagers grades will be a normal distribution because 85>30.
Formula
A confidence interval is comprised of two parts: a point estimate and a margin of error.
Point Estimate ± Margin of error
Point Estimate ± (t*) (standard error)
Point Estimate
A point estimate is a single value that is used to estimate a population parameter. For example, if you are trying to estimate the mean of a population, the point estimate would be the sample mean (aka x̄).
The point estimate is the middle of the confidence interval, and it is the best estimate of the population parameter based on the sample data. In this case, if you're trying to estimate the mean of a population using a sample of data, you would calculate the sample mean as the point estimate.
The confidence interval would be calculated based on the sample mean and the standard error of the mean, and it would be constructed so that there is a 95% (or another percentage value set by the person in charge of the statistical analysis) chance that the population mean falls within the interval.
Margin of Error
A margin of error can be thought about as a "buffer zone." It is the amount that we add and subtract to our sample mean to give some room for error in estimating our population mean. It is made up of two parts:
- Critical Value
- Standard Error
The critical value is the t-score based on the mean and standard deviation of the sampling distribution, along with the degrees of freedom. Degrees of freedom can be calculated by taking the sample size and subtracting one. Since we have a distribution that is only approximately normal, the degrees of freedom allow us to adjust our calculations based on how small or large our sample is. If we had an infinite sample size, we would have a perfect normal curve (which would call for us to use a z-score). A critical value can be calculated using either a calculator's inverse T function or using the charts on the College Board provided formula sheet. 📄
Meaning of Confidence Interval
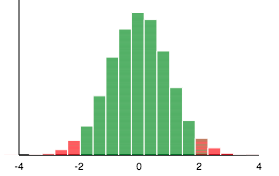
image provided by: rossmanchance.com
A confidence interval is a range of values that we believe the true population mean will fall between. In the example above, we have a 95% confidence interval when given a sample mean of 0, sample standard deviation of 10 and a sample size of 100. The graphic shows this sampling distribution and how only 5% of the samples would fall outside of the (-2, 2) range. Hence, we can be 95% confident that the true population mean is somewhere between -2 and 2. 😎
Interpretation
On the AP exam, you are typically asked to create and interpret a confidence interval. 🔨
When asked to do this for a population mean, interpret your interval using the following template:
"I am ___% confident that the true population mean of ______________ is between (___, ___)."
Rubrics generally include the following three aspects:
- Confidence level
- Context of problem
- Demonstrates knowledge that we are inferring about the true population mean
🎥 Watch: AP Stats - Inference: Confidence Intervals for Means
Browse Study Guides By Unit
👆Unit 1 – Exploring One-Variable Data
✌️Unit 2 – Exploring Two-Variable Data
🔎Unit 3 – Collecting Data
🎲Unit 4 – Probability, Random Variables, & Probability Distributions
📊Unit 5 – Sampling Distributions
⚖️Unit 6 – Proportions
😼Unit 7 – Means
✳️Unit 8 – Chi-Squares
📈Unit 9 – Slopes
✏️Frequently Asked Questions
📚Study Tools
🤔Exam Skills

Fiveable
Resources
© 2025 Fiveable Inc. All rights reserved.