📚

All Subjects

♾️

AP Calc

👀

Unit 4

4.9 MC Answers and Review

4 min read•january 1, 2022

AP Calculus AB/BC ♾️

279 resources

See Units

Answers and Review for Differentiation: Contextual Applications of the Differentiation

Image from Wikimedia Commons

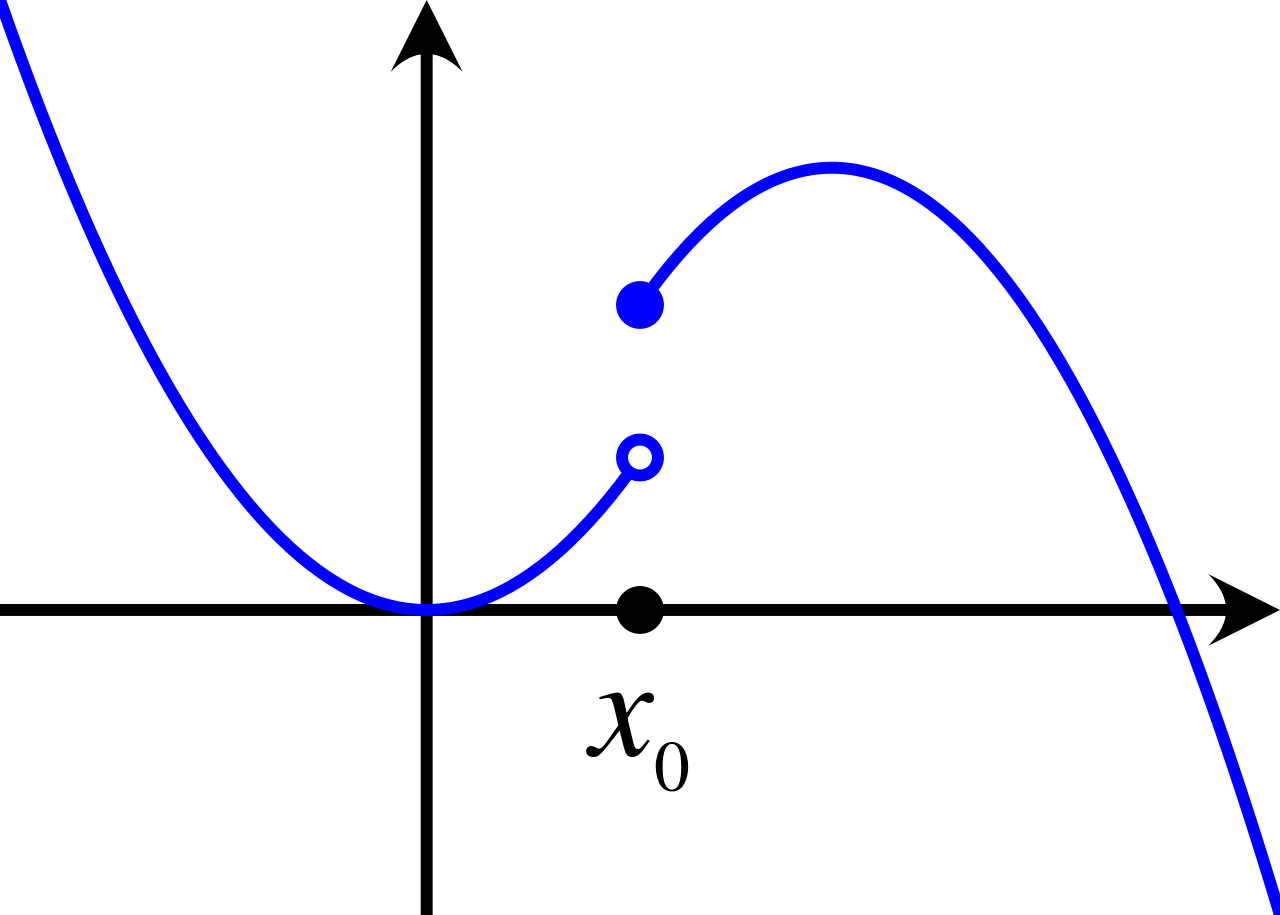
⛔STOP!⛔ Before you look at the answers make sure you gave this practice quiz a try so you can assess your understanding of the concepts covered in unit 1. Click here for the practice questions: AP Calculus Unit 4 Multiple Choice Questions. Facts about the test: The AP Calculus exam has two sections of multiple choice: 30 questions in 60 minutes with no calculator, and 15 questions in 45 minutes with a calculator. *The following questions were not written by CollegeBoard and although they cover information outlined in the AP Calculus Course and Exam Description the formatting on the exam may be different.

B is correct because remember the units are represented by dy/dx or f(x)/x. To represent the units you will need to place the t units/m units.

📄 Study Unit 4.2: Straight-Line Motion: Connecting Position, Velocity, and Acceleration

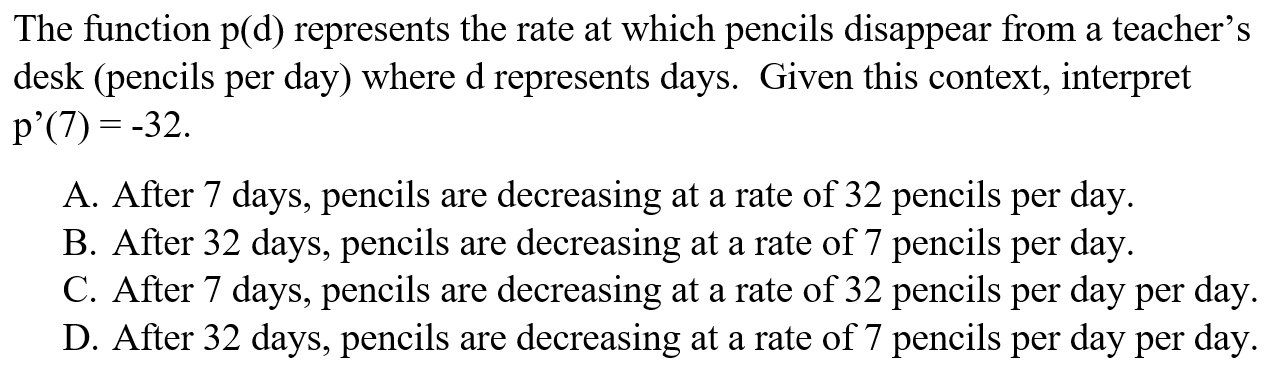
C is correct because to accurately represent the units, make sure to determine if the initial value is already a rate. In this case, p(d) is given as a rate. Therefore, p'(d) is taking the derivative of a rate.

📄Study Unit 4.3: Rates of Change in Applied Contexts other than Motion

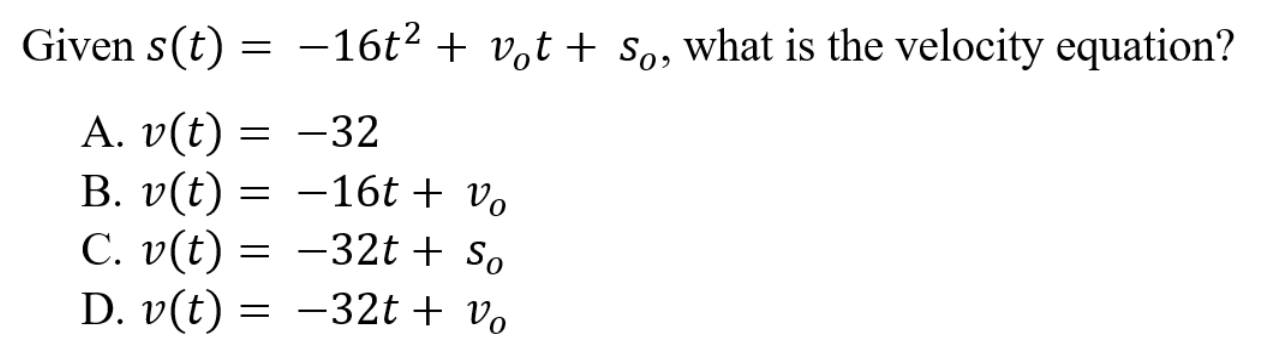
D is correct because velocity, v(t), is the derivative of position, s(t). The derivative is taken in respects to time. Initial velocity and position are assumed to represent constants.

📄 Study Unit 4.2: Straight-Line Motion: Connecting Position, Velocity, and Acceleration

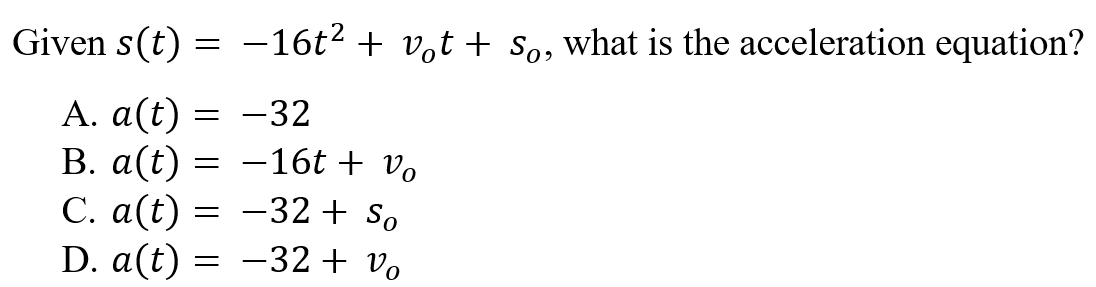
A is correct because acceleration, a(t), is the second derivative of position, s(t). The derivative is taken in respects to time and nets a constant.

📄 Study Unit 4.2: Straight-Line Motion: Connecting Position, Velocity, and Acceleration

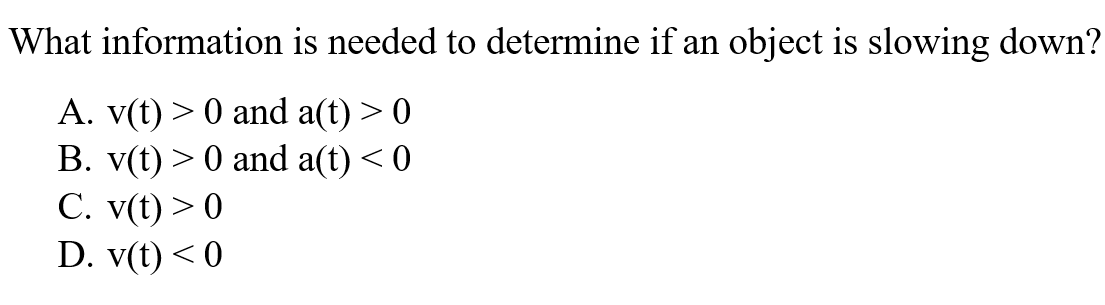
B is correct because to determine if an object slowing down, velocity and acceleration are going in opposite directions. Both acceleration and velocity are needed to determine if an object is slowing down.

📄 Study Unit 4.2: Straight-Line Motion: Connecting Position, Velocity, and Acceleration

D is correct because velocity is speed with direction. When v(t) changes signs, the direction changes.

📄 Study Unit 4.2: Straight-Line Motion: Connecting Position, Velocity, and Acceleration

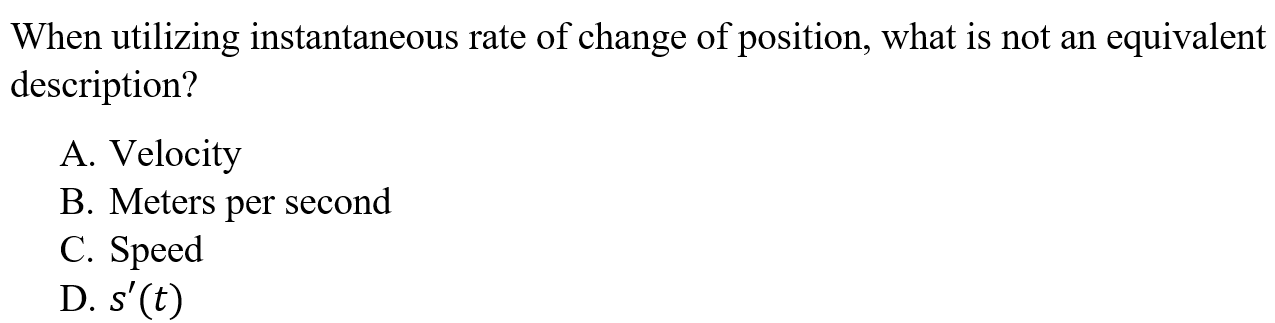
C is correct because the instantaneous rate of change for position is equivalent to velocity, s'(t), and the meters per second. Speed is velocity without direction.

📄 Study Unit 4.2: Straight-Line Motion: Connecting Position, Velocity, and Acceleration

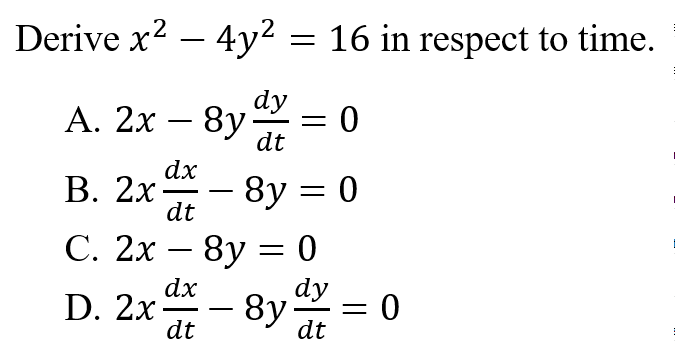
D is correct because when deriving in respects to time, each variable must be divided by time. This causes all variables except for time to exists as a rate.

📄 Study Unit 4.4: Intro to Related Rates

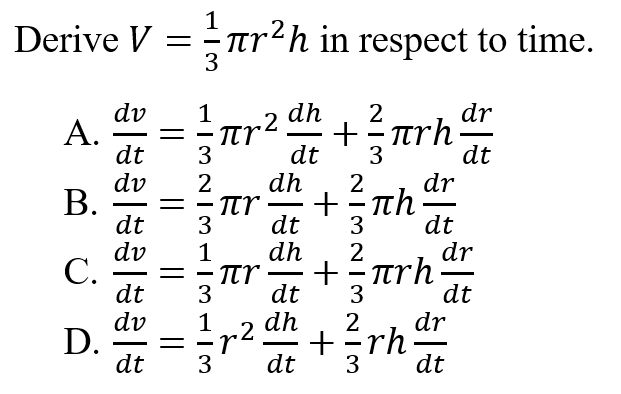
A is correct because when deriving in respects to time, each variable must be divided by time. All derivatives rules must be followed. In this example, the product rule must be executed.

📄 Study Unit 4.4: Intro to Related Rates

10.

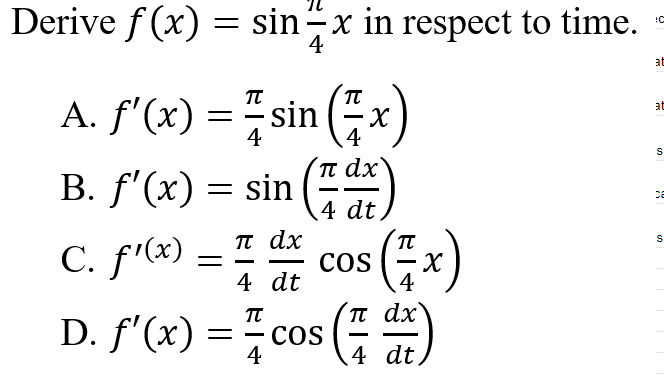
C is correct because deriving in respects to time involves keeping the previous derivative rules intact while keeping the rates. In this case, you will need to execute a chain rule which results in a dx/dt being multiplied by the derivative of sin x which equals cos x.

📄 Study Unit 4.4: Intro to Related Rates

11.

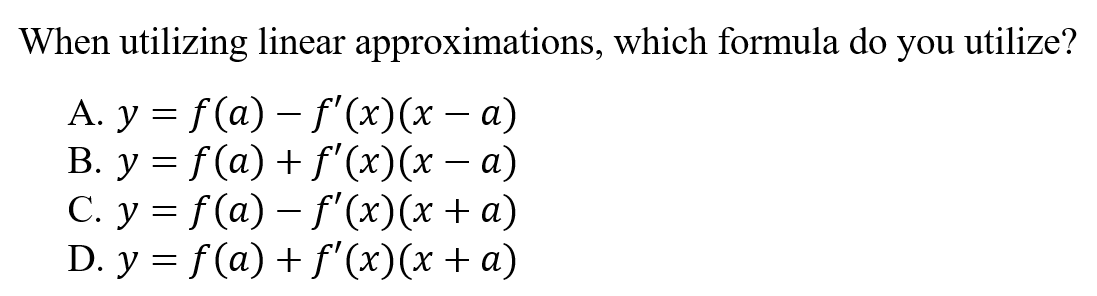
B is correct because linear approximation is a variation of the point-slope form. Linear approximation can be utilized to find an estimation when a function is not given.

📄 Study Unit 4.6: Approximating Values of a Function Using Local Linearity and Linearization

12.

A is correct because linear approximations consist of a variation of the point-slope formula. Within this formula, the y-coordinate of the original function is added to the product of the slope at x and the difference of the estimated value and x.

📄 Study Unit 4.6: Approximating Values of a Function Using Local Linearity and Linearization

13.

B is correct because L'Hopital's Rule is utilized when determining the result of the limit y direct substitution is the indeterminate form. To determine the limit, you can derive the numerator and denominator then substitute in c.

📄 Study Unit 4.7: Using L'Hopitals Rule for Determining Limits in Indeterminate Forms

14.

D is correct because L'Hopital's Rule can be utilized with indeterminate form. For choice D, 0/4 = 0 which not an indeterminate form.

📄 Study Unit 4.7: Using L'Hopitals Rule for Determining Limits in Indeterminate Forms

15.

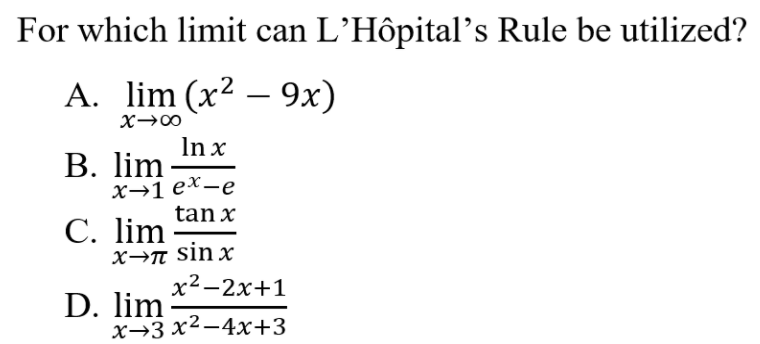
B is correct because L'Hopital's Rule is used when an indeterminate form is present after direct substitution when trying to determine a limit. You would need to directly substitute into each limit. Choice B is the only one that results in the indeterminate form.

📄 Study Unit 4.7: Using L'Hopitals Rule for Determining Limits in Indeterminate Forms